化歸思想在高中數學函數學習中的運用

摘?要：在高中數學教學板塊中，函數作為一個重要內容，其本質就是客觀描述世界中的變化規律。采用化歸思想融入高中數學函數教學方法中，能夠有效地激發高中生的化歸思想意識，提升其解題能力，大大增強課堂教學成效。文章立足于化歸思想的概念、意義和運用原則，對高中數學中相關的函數試題進行探討，舉例提出了化歸思想的主要應用方法。

關鍵詞：化歸思想;高中數學;函數教學

化歸思想的運用形式就是將繁雜的問題劃歸為簡單的方式進行處理，幫助學生從表面上看似不理解或者是具有一定難度的函數題轉化為簡單的問題。函數作為高中數學教學的重要內容，幫助學生積極運用化歸思想，掌握相應的解題技能，不僅能夠進一步理解函數的相關規律，熟練靈活的解決函數難題，還能提升學生的思維能力，促進數學核心素養的發展。

一、 化歸思想概述

化歸思想就是指個體在解決某些難題的時候，將需要解決的問題逐步轉化成為個體已經掌握的知識點，通過分解形式間接的計算出主要問題的正確結果，達到刪繁就簡的目的。在高中數學函數教學中，運用化歸思想的主要優勢就是能夠幫助學生將復雜的問題規范化、模式化，將學生感到困難的問題轉換為學生已有的認知經驗來計算。在運用化歸思想的過程中，應當注意轉換問題的條件，從中提取具有核心價值的信息，通過各種條件、結論和過程的轉化，使得那些讓學生手足無措的題目，漏出其本來的面目，從而方便學生正確解題，獲得高分。

二、 化歸思想在高中數學函數學習中的意義

（一）鞏固和深化函數知識

高中數學函數知識的教學更加側重于對學生數學思想方法的培訓，運用化歸思想能夠進一步有將各種函數題型中難以理解的原理和相關規律逐步分解，讓學生更加容易掌握。學生在對各個分解的小問題逐一解答的過程中，能夠對知識進行全面的分析，從而不斷強化化歸思想的使用方法，有效地鞏固和深化學生的函數知識和解題能力。

（二）培養數學的學習思維

運用化歸思想不僅能夠有效地讓學生更容易掌握函數知識，還能夠讓學生明白數學的價值，開拓數學思維，進而將數學解題技能靈活遷移到生活實際中。通過課堂上詳細系統的學習和總結，學生在腦海中構建函數知識框架，并從復雜的知識點中探索規律，在潛移默化中養成良好的數學思維能力。

（三）培養數學的分析能力

學生運用化歸思想能夠將煩瑣的問題簡單化，能夠自主進行探索分析，不斷提升自己解決數學問題的能力，提升數學綜合水平。從而將數學方法進行綜合，鞏固了所學知識，數學的分析能力也獲得提升。

三、 化歸思想在高中數學函數教學中的運用原則

（一）熟悉化原則

對于高中生來說，其已經具備了一定的基礎知識，且形成了獨立的認知規律，個體的學習是將未知的問題轉換為熟悉的已知問題。也就是說，將化歸思想運用在高中數學函數教學中，就是要將新概念納入個體的已知結構中，構建個體熟悉的解題模型，才能順利的實施到下一步的解題步驟中。

（二）簡單化原則

顧名思義，簡單化原則就是將復雜的問題和知識轉換為簡單的形式，在不同的問題情境中，化歸思想的運用都不能夠盲目的進行，而是應當積極保證化歸目標的簡單性，通過簡單的轉化使得后續的解題過程更加簡單。

（三）具體化原則

在學習新知識的過程中，個體對于任何事物生動直觀的感受比抽象的理解能加容易達到預期目標。化歸思想的運用就是一個抽象到具體的過程，通過難懂的理論文字表述，從中提煉有效信息，然后運用直觀的圖形表示出來，給個體一目了然的感覺，將問題中各個變量之間的關系變得具體清晰，更加容易把握其中的規律和有效信息。

（四）和諧統一性原則

對于高中數學知識來說，其更加關注于學生的思維模式，所以通常情況下，給出問題的條件比較雜亂，給學生的思考帶去一定的挑戰。學生在這個時候就需要有意識地將各個問題數據的表現形式變得和諧，將各個變量和結構之間的關系變得統一。運用化歸思想的和諧統一原則，從而在體現數學美的基礎上，更加便于正確求解方式。

（五）形式標準化原則

形式標準化原則具體來講就是標準化的模式科學，高中數學知識包含了公式、法則、定理等，例如在教學函數內容時，學生往往就會運用到相關公式法則。又如，圓錐曲線對應的圖像和幾何性質也是針對標準方程制定的。這種將某一種問題朝著標準的形式轉化的方法就叫作形式標準化原則。

（六）低層次化原則

在學生分析高層次的數學問題時候，應當引導其有意識地將相關條件劃歸為更加直觀簡單的低層次問題，這種方式能夠將具有難度的問題變得簡單化，方便學生求解。例如，對高維空間問題與高次問題分別進行降維、降次處理，對含多個變元的問題消元轉化為變元稍少的問題，這種降低問題復雜性的方式就是低層次化原則。

四、 化歸思想在高中數學函數學習中的主要運用

（一）化歸思想在函數中的動靜間轉化

在高中函數學習過程中，教師需要引導學生不斷發現問題，深入挖掘各個變量之間的依賴關系，探尋生活中的具體規律，從文字數據中提煉具有關鍵性的因素，并準確的明晰各個抽象變量之間的關系。學生通過學習之后，能夠從中得知函數的單調性和最值等，循序漸進的解決相關問題，獲得舉一反三的能力。這樣一個構造函數的過程就是化歸思想在函數中的動靜轉化過程。

教師可以將這道題作為函數動靜轉化的典型案例，從題目中我們能夠得知，觀察log312與log35是兩個靜止的數值，學生通過認真思考能夠發現這兩個值均為對數形式，基于這一基礎例題，教師就可以構造相應的函數實現由靜到動的轉化。

（二）化歸思想在函數中的數形間轉化

在函數學習的過程中，函數圖像是其主要的標識方法之一，學生應當對不同的函數圖像了然于心，并以此來探討相應的函數性質。運用化歸思想達到數形結合的目的，再用數形結合的方法巧妙地將函數的解析式和函數圖像結合起來，從而將困難的問題轉化為簡單的題目，學生一眼就能夠看出其中的規律，找到解題的突破口。

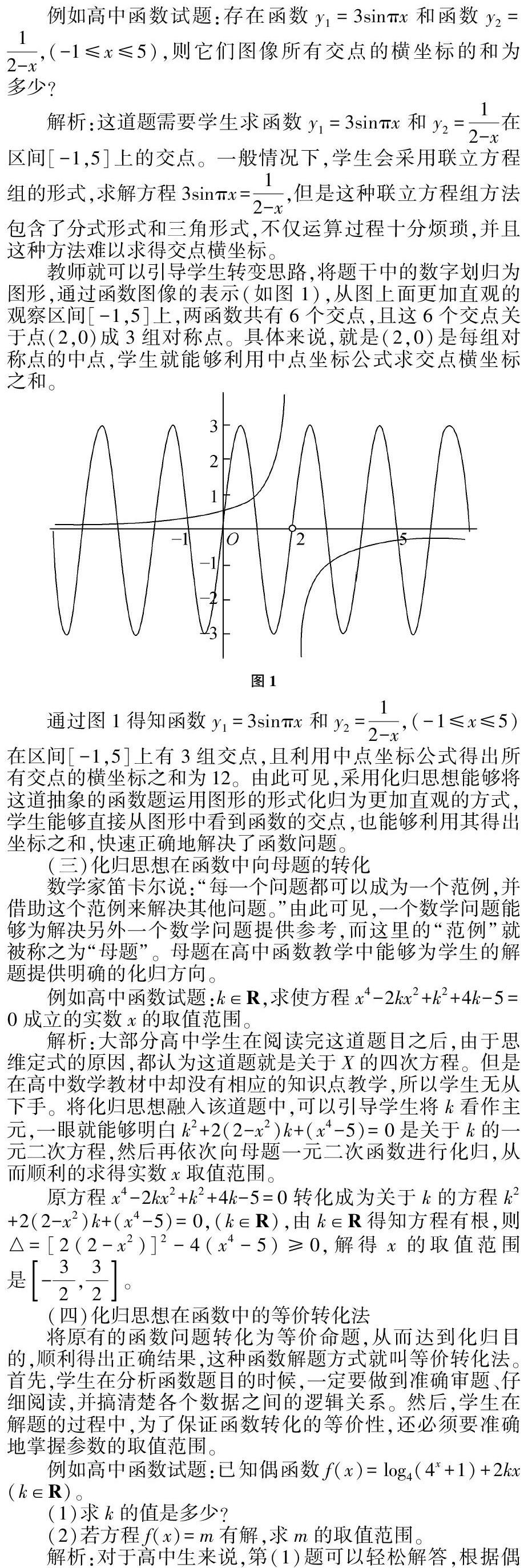
教師就可以引導學生轉變思路，將題干中的數字劃歸為圖形，通過函數圖像的表示（如圖1），從圖上面更加直觀的觀察區間[-1，5]上，兩函數共有6個交點，且這6個交點關于點（2，0）成3組對稱點。具體來說，就是（2，0）是每組對稱點的中點，學生就能夠利用中點坐標公式求交點橫坐標之和。

（三）化歸思想在函數中向母題的轉化

數學家笛卡爾說：“每一個問題都可以成為一個范例，并借助這個范例來解決其他問題。”由此可見，一個數學問題能夠為解決另外一個數學問題提供參考，而這里的“范例”就被稱之為“母題”。母題在高中函數教學中能夠為學生的解題提供明確的化歸方向。

（四）化歸思想在函數中的等價轉化法

將原有的函數問題轉化為等價命題，從而達到化歸目的，順利得出正確結果，這種函數解題方式就叫等價轉化法。首先，學生在分析函數題目的時候，一定要做到準確審題、仔細閱讀，并搞清楚各個數據之間的邏輯關系。然后，學生在解題的過程中，為了保證函數轉化的等價性，還必須要準確地掌握參數的取值范圍。

（五）化歸思想在函數中的換元法

針對高中函數板塊中的整式、有理式，個別學生可能會覺得有一定難度，那么就是就可以采用換元法，幫助學生對題目進行簡化或降冪處理。在使用換元法的時候，一定要注重各個參數取值的范圍，避免馬虎出現誤差，降低了解題結果的準確性。與此同時，學生要確保換元前后的參數取值范圍統一，進一步把握換元法使用的關鍵點，靈活熟練的對其運用。

分析：通常情況下，學生通過閱讀題干就能夠找出解題思路。但是為了確保計算結果的準確性，教師在解析講解的時候就可以借助換元法對其加以處理。

五、 結語

化歸思想作為高中數學教學中的一種重要的思想方法，其可以融入數學知識的方方面面。由于高中數學函數題目本身就具備較大的差異，且各個題目都具有各自本身的特點，教師為了提升課堂教學質量，提升學生解題技能，就應當積極滲透化歸思想，讓學生通過分析函數的特點，找到問題的切入點，并深入感受化歸思想的具體運用，最終促使學生數學綜合能力得到全面發展。

參考文獻：

[1]楊志遠.化歸思想在高中數學函數教學中的應用探究[J].數學學習與研究，2019（15）：21.

[2]甘光虎.借助化歸思想?促進高中數學函數教學[J].數學學習與研究，2019（11）：136.

[3]鄧志強.化歸思想在高中數學函數教學中的運用及實踐研究[J].數學學習與研究，2019（5）：30.

[4]張元垚.化歸思想在高中數學函數學習中的運用[J].科技經濟導刊，2019，27（1）：137+136.

[5]甘甜.化歸思想在高中數學函數學習中的運用[J].農家參謀，2017（16）：84.

作者簡介：

朱艷燕，上海市，上海市曹楊第二中學。