HPM視角下的“基本不等式”同課異構課例分析

趙麗紅 汪曉勤

【摘?要】運用HPM課例分析框架，對HPM視角下“基本不等式”的兩節課進行比較和分析。兩節課都運用了豐富的數學史素材，這些素材符合科學性、可學性、趣味性和人文性等原則。在史料的運用上，其中一節課采用了附加式、復制式、順應式和重構式，而另一節課只采用了前三種方式。在數學史的融入上，兩節課均體現了方法之美、探究之樂、能力之助、文化之魅和德育之效的教育價值。在融入的自然性上，其中一節課由于未采用重構式，因而未能體現知識之諧，所用史料對部分教學目標的達成作用不大，未滿足有效性要求。

【關鍵詞】HPM;基本不等式;同課異構;數學文化

【作者簡介】趙麗紅，華東師范大學教師教育學院在讀碩士研究生，主要從事數學史與數學教育研究;汪曉勤，教授，博士生導師，HPM工作室主持人，主要從事數學史與數學教育研究。

【基金項目】上海高校“立德樹人”人文社會科學重點研究基地之數學教育教學研究基地研究項目——數學課程與教學中落實立德樹人根本任務的研究（A8）

一、引言

“基本不等式”是滬教版數學教材高一上冊第2章“不等式”的第4節內容。在學習本節內容之前，學生在初中不等式知識的基礎上學習了一元一次不等式、一元二次不等式及其他不等式的基本性質和解法，具備一定的代數運算基礎。教材的引入方式是引述客觀世界中一些恒成立的不等關系，進而直接呈現基本不等式，然后用作差法進行代數證明，再用趙爽“弦圖”給出幾何解釋。這里，教材雖然運用了數學史，但“弦圖”原本是用來證明勾股定理的，數學史上的基本不等式并非源于弦圖。因此，我們尚需運用更恰當的數學史料，去揭示基本不等式產生的真正動因，從而更好地激發學生的學習動機。

HPM視角下的數學教學，在設計上，關注學生的學習動機與認知起點，選擇恰當的數學史料、創設具有歷史底蘊的情境、揭示知識產生的必要性并增加知識的趣味性。在實施上，力求將數學史自然而然地融入課堂教學。在評價上，從知識維度看知識之諧和方法之美，從過程維度看探究之樂和能力之助，從情感維度看文化之魅和德育之效。隨著HPM教學理念的傳播和HPM教學案例的增多，越來越多教師對HPM產生濃厚的興趣，HPM視角下的同課異構現象進入人們的視野。

對于“基本不等式”這一課題，來自上海市兩所不同高中的教師A和教師B精心選擇相關的歷史素材，各自從HPM視角進行教學設計。本文運用HPM課例分析框架，對兩節課在數學史料的選擇、融入方式、運用效果等方面的異同點進行比較和分析，以期為HPM課例研究提供參考。

二、基本不等式的歷史素材

（一）古希臘數學文獻

公元前6世紀，畢達哥拉斯學派已研究過算術中項、幾何中項與調和中項。后來，尼可麥丘和帕普斯統一了各類中項的定義。歐幾里得《幾何原本》第2卷命題5稱：將一條線段二等分，再分成不相等的線段，則由二不相等的線段構成的矩形與兩個分點之間一段上的正方形之和等于原線段一半上的正方形[1]。設不等的兩條線段長分別為a和b，上述命題相當于一個代數恒等式，即ab+b-a22=a+b22。

歐幾里得的證明思路是“將矩形化為等積的矩尺形，再將其補成正方形”（如圖1），由上述恒等式可得不等式：ab0，b>0，a≠b）①，ab0，b>0，a≠b）②。

公元前2世紀左右，古希臘數學家芝諾多魯斯著《論等周圖形》一書，給出了以下命題：“在邊數相同的等周多邊形中，等邊且等角的多邊形面積最大”[2]。考慮長為b、寬為a的矩形以及與之等周的正方形，即得不等式①或②。

公元3世紀末，古希臘數學家帕普斯在同一個半圓上作出了三類中項。如圖2，以AB為直徑作半圓ADB，CDSymbol^A@

AB，OD為半徑，CESymbol^A@

OD，則OD、CD和DE分別為AC和CB之間的算術、幾何和調和中項[3]61。

（二）?中國古代數學文獻

公元3世紀，趙爽在給《周髀算經》“勾股圓方圖”作注時，給出“大方圖”（如圖3）[3]62。設Rt△EBF的勾、股、弦分別為a、b、c，則有（a+b）2=（b-a）2+4ab，（a+b）2=2c2-（b-a）2=2（a2+b2）-（b-a）2，因此可得不等式4ab≤（a+b）2≤2（a2+b2）。

圖2

圖3

《九章算術》勾股章中設題：“今有勾五步，股十二步，問勾中容方幾何。”其解法是：“并勾股為法，勾股相乘為實，實如法而一，得方一步。”[4]劉徽利用出入相補原理證明了上述公式。如圖4，用對角線將長和寬分別為a和b的矩形分成兩個直角三角形，并用不同顏色標記不同類型的圖形，得到“勾股容方圖”。將圖形重組，形成矩形（如圖5），即得出與直角三角形共直角的內接正方形邊長為d=aba+b。

圖4

圖5

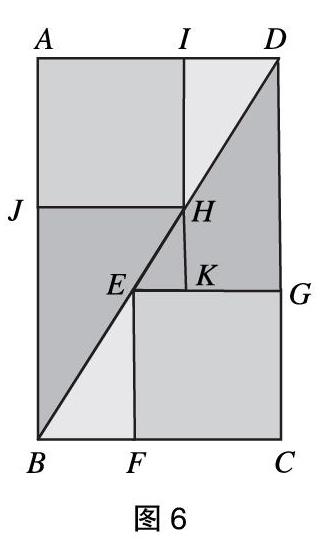
利用“勾股容方圖”，可以導出均值不等式。如圖6，延長IH交EG于點K，得到Rt△HKE。由三角形的相似性，易得HK=b-2aba+b，KE=2aba+b-a。由CD?>?CB，得HK?>?KE，故b-2aba+b>2aba+b-a，即2aba+b

圖6

（三）相關應用

1471年，德國數學家雷吉奧蒙塔努斯在給愛爾福特大學羅德教授的信中提出問題——一根垂直懸掛的桿子，從地面上哪一點看上去它最長？[5]即“最大視角”問題，這被稱作數學史上的第一個極值問題。

16世紀，意大利建筑大師帕拉第奧認為建筑的美產生于形式，他在著作《建筑四書》中指出，具有一定形式和比例的房間是優美的[6]。他給出了優美房間的長、寬和高所滿足的規則，其中有兩類房間的高分別等于長和寬的算術中項與幾何中項。

三、兩節課的宏觀比較

（一）教學目標和重難點

兩節課共同的教學目標如下。

（1）了解數學史料，經歷基本不等式的探究與發現過程;

（2）掌握兩個基本不等式及其應用前提，并利用它們求解最值問題;

（3）通過最值的應用，理解基本不等式在實際生活中的應用與重要性。

不同之處在于，教師A注重讓學生去親歷基本不等式產生的過程，培養學生邏輯推理、直觀想象和數學建模的素養，使學生理解基本不等式的意義;教師B則著重從歷史上的數學問題出發，讓學生在探究中發現基本不等式，領悟轉化的思想、品味數學文化。

兩節課的教學重點和難點也是一致的。

（1）教學重點：基本不等式的證明方法與應用前提;

（2）教學難點：基本不等式的幾何探究及其在最值問題中的靈活應用。

（二）教學過程

教師A和教師?B?的教學過程主要分為情境創設、證明探究、新知應用、課堂小結和布置作業五個環節，具體內容見表?1。

從表1可以看出，教師A和教師B均從HPM的視角進行教學，相同之處在于以學生（激發興趣）、活動（合作探究）、方法（數形結合）、文化（中西交融）、應用（走向生活）為著眼點。不同之處在于，教師A從生活的角度出發、關注學生的認知起點，蹦床公園中的海綿池形狀改建的教學情境具有歷史文化底蘊，引入比較自然;接著在證明探究環節，自然過渡到歐幾里得的命題，基本不等式發生與發展的過程順暢且貼切。教師B直接從歷史角度出發，用蘊含算術、幾何中項的建筑引入;在證明探究環節，借助“勾股容方”問題及其解法導出基本不等式，整個過程散發濃郁的數學文化氣息，創新性較強。

四、兩節課的微觀比較

以下從史料的適切性、融入的自然性、方法的多樣性和價值的深刻性[7]對兩節課進行微觀比較。

（一）史料的適切性

在?HPM?實踐中，史料的選取原則有科學性、趣味性、有效性、可學性和人文性[8]。本文按照教學環節來分析史料的適切性，見表2。

由于HPM專業學習共同體實現數學史資料共享，教師A和教師B所用的素材來自高校研究者的歷史研究，其科學性均得到保障。教師A在情境創設環節引入蹦床公園中海綿池的改建問題，體現了趣味性、可學性和有效性。在證明探究環節，歐幾里得幾何圖形為引出基本不等式創造了條件，體現了可學性和有效性。在新知應用環節，引入數史上第一個極值問題——“最大視角”問題，體現基本不等式的應用，雖符合有效性和趣味性原則，但由于該問題的求解需要利用和角正切公式，不符合學生的知識基礎，缺乏可學性。接著用微視頻介紹趙爽的“大方圖”，引起學生好奇，富有趣味性和人文性;補充的證法增進學生對基本不等式的理解，體現有效性。拓展作業涉及帕普斯的半圓模型，為學生提供進一步探究基本不等式的機會，符合可學性和有效性原則。

教師B在情境創設環節引入算術中項與幾何中項的建筑背景，體現了人文性;帕拉第奧“好房間”所涉及的兩類平均數，為基本不等式的探究做好了鋪墊，體現了趣味性和人文性。在證明探究環節，提出“勾股容方”問題，并介紹劉徽的證明方法，為基本不等式的推導創造了條件，符合可學性和人文性原則，但有效性體現不足。

（二）融入的自然性

要將數學史自然地融入數學教學，教師需要將知識的歷史序、邏輯序和學生的心理序有機統一。以下是兩位教師的教學片段與評析。

1教師A的教學片段

師：正方形海綿池與長方形海綿池有什么關系？

生：周長相等。

師：其實這就是歷史上的等周問題，古人很早就進行了研究。從課前問卷中可看到有的古人認為周長越長，面積就越大，你覺得古人的想法合理嗎？

生：不合理。

師：那么他們如何探究這個問題呢？古代數學家并不會代數解法，他們其實是借助了幾何作圖。今天我們就追尋古人的足跡，進行小組合作、利用尺規作圖截出正方形的邊長，探究長方形與正方形的面積關系。

（小組探究活動之后，學生代表分享了作圖方法，教師A借助幾何畫板進行直觀演示。）

師：同學們發現了什么？

生：長方形面積比正方形面積小。

師：能用簡單的式子表達嗎？

生：當a≠b時，ab

師：非常好，大家從幾何模型抽象出了這個代數表達式，那么它背后隱含的幾何意義是什么呢？

生：周長相等的矩形中正方形的面積最大。

師：對，這就是我們今天要研究的基本不等式。

評析：關于基本不等式，教材中采用的邏輯體系是從一般的不等關系、代數不等式及其解法到基本不等式。在這樣的邏輯體系中，基本不等式只是作為特殊的不等關系出現，因而教材無意去探求其背后的動因。從歷史來看，等周問題是導致基本不等式誕生的動因之一，教師A借助海綿池面積問題引出基本不等式，符合歷史序。關于等周長方形和正方形面積的大小關系，學生在小學和初中階段已有接觸，因此該情境符合學生的認知基礎。同時，教師A在課前問卷中介紹了古人對周長和面積關系的誤解，再加上課上提出的實際問題，有效地激發了學生的學習欲望。事實上，當教師在課堂上再現知識的歷史動因時，往往就激發了學生的學習動機。另一方面，從海綿池形狀變更前后的幾何模型，學生實際上建立了長方形與正方形面積之間的恒等式，因而遵循了“從等式到不等式”的邏輯序。可見，在教師A的課堂上，數學史的融入是比較自然的，基本實現了邏輯序、歷史序和心理序的統一。

2教師B的教學片段

師：同學們知道了出入相補原理，接下來進行小組合作，把“勾股容方圖”拆開來重新拼，求出正方形的邊長x。

（活動之后，各小組展示了幾類長方形的拼圖方案。）

師：很棒，這就是古代數學家劉徽的做法。同學們求出x是多少？

生：x=aba+b。

師：這種方法非常簡潔，接下來我們繼續研究“勾股容方圖”中的Rt△HKE（如前文圖6），試試看，能否求出兩條直角邊？

生：能。

師：好，請同學們說說思路。

（兩名學生分享了自己的做法：一名學生利用相似三角形法，另一名學生利用各邊長之間的數量關系做差求解，兩名學生都得出HK?=?b-2x，KE=2x-a。）

師：HK與KE之間有什么數量關系呢？

生：HK?>?KE。

師：為什么？

生：因為Rt△HKE與Rt△DCB相似，而CD?>?CB。

師：很好，那么大家把正方形的邊長代入HK?>?KE中，看看式子能不能化簡？

生：化簡得ab

師：還能發現什么？

生：兩邊開方，得出幾何平均數小于算術平均數。

評析：教師B從劉徽的“勾股容方圖”出發，引導學生先求出直角三角形內接正方形的邊長，然后根據直角三角形的相似性，從直角三角形兩直角邊的大小關系得出基本不等式，遵循“從幾何上的不等關系到代數上的不等關系”的邏輯序，具有創新性。但是，劉徽的“勾股容方圖”本身并非是基本不等式產生的歷史動因，就像趙爽“弦圖”初衷也無關基本不等式一樣。如今“勾股容方圖”和“弦圖”也被用于基本不等式的證明。相比較而言，“弦圖”顯然比“勾股容方圖”更直觀。因此，雖然教師B的設計很創新，但從“勾股容方圖”到基本不等式，并不符合歷史序，也未能有效地揭示基本不等式產生的動因，因而也不符合學生的心理序。可見，在教師B的課堂上，數學史的融入在自然性上打了折扣。

（三）方法的多元性

數學史融入教學有四種方式：附加式、復制式、順應式和重構式。

教師A首先從海綿池的改建方案中抽象出長方形等周問題，引導學生用尺規作圖法作出與長方形等周的正方形，從中探究等周正方形與長方形的面積關系;接著用代數形式來表征上述關系，得出代數恒等式;最后從恒等式中得出基本不等式。因此，教師A重構了基本不等式的產生過程。學生在探究過程中所借助的幾何模型，實際上是《幾何原本》中命題所涉及圖形的改編，是數學史料的順應式運用。在新知應用環節，復制式地采用了雷吉奧蒙塔努斯的“最大視角”問題。通過微視頻介紹趙爽的“大方圖”以及基本不等式的相應證明，屬于附加式。利用帕普斯半圓模型設計探究任務，也是數學史料的順應式運用。

教師B結合學生課前觀看的建筑視頻，首先附加式地引出帕普斯的算術中項與幾何中項定義。接著，讓學生計算帕拉第奧“好房間”中與高相關的兩類平均數，是數學史料的順應式運用。然后，復制式運用“勾股容方”問題讓學生求解。在學生交流解決方案之后，教師B介紹劉徽的原始解法，建立古今聯系，是歷史上問題與解決方法的復制式運用。教師B借助“勾股容方圖”，引導學生進一步探究直角三角形的邊長關系，最后導出基本不等式，是數學史料的順應式運用。最后，在新知應用環節，改編帕拉第奧“好房間”中與高相關的問題，并以等周問題為背景設置應用題，也屬于順應式。

可見，在教師A和教師B的課堂上，數學史的運用方式都是多元的，但教師A運用了重構式，而教師B沒有。

（四）價值的深刻性

數學史融入數學教學的教育價值主要有六種：知識之諧、方法之美、探究之樂、能力之助、文化之魅和德育之效。

1教師A的教學

在知識維度上，教師A重構了基本不等式的發生和發展過程，構建了知識之諧。在證明探究環節，歐幾里得的幾何方法、微視頻所呈現的基于“弦圖”和“勾股容方圖”的幾何證法，彰顯了方法之美。

在過程維度上，教師A綜合借鑒歷史上的等周問題以及《幾何原本》中的命題來設計探究活動;基于數學史的幾何方法有助于培養學生的直觀想象、邏輯推理和數學抽象素養;提供的課后拓展材料也有助于提升學生的閱讀能力，體現了探究之樂和能力之助。

在情感維度上，從歐幾里得作圖法到趙爽的“弦圖”、從等周問題到“最大視角”問題，既有中西文化的交融，又有數學文化對生活的啟示，展示了文化之魅[9]。探究活動之后，教師A將學生的方法與歐幾里得方法進行對照，提升了學生學習數學的自信心。問卷調查表明，等周問題讓學生感悟到數

學背后的理性精神。此外，數學史的融入激發了學生的學習興趣。因此，教師A借助數學史達成了德育之效。

2教師B的教學

在知識維度上，雖然教師B從建筑的角度引入，設計比較新穎，但算術平均數與幾何平均數的定義以及兩者的關系是直接提出來，比較突兀，在知識之諧的構建上有待改進。在證明探究環節，教師B利用“勾股容方圖”，引導學生發現基本不等式，彰顯了方法之美。

在過程維度上，“勾股容方”問題為學生提供了探究機會，也有助于培養學生的直觀想象和邏輯推理素養，體現了探究之樂和能力之助。

在情感維度上，設計的情境充滿數學文化味，既讓學生感受到數學與建筑之間的聯系，又體會到數學背后的多元文化，展示了文化之魅。從問卷調查可知，“勾股容方圖”給學生帶來新奇的感受，激發了他們的學習興趣。而且，中國古代的“勾股容方”有助于學生了解中國古代的數學文化。因此，教師B的課堂蘊含了比較豐富的德育元素，達成了德育之效。

五、結語

綜上分析可知，教師A和教師B所用的史料都比較豐富，符合科學性、趣味性、可學性和人文性原則，但教師B所用史料的有效性不足。教師A和教師B運用數學史的方式均有附加式、復制式和順應式，教師A還運用了重構式。教師A重在重構基本不等式的發生與發展過程，基本實現了邏輯序、歷史序和心理序的統一，融入較為自然;教師B注重基本不等式的幾何探究與推導過程，呈現了清晰的邏輯序，但未能兼顧歷史序和心理序。在兩節課中，數學史都體現了多元的教育價值，但由于教師B未采用重構式，在追求教學設計創新的同時忽略了知識之諧的構建。

通過對兩節課的比較和分析，我們得到以下啟示。

1數學史融入數學教學，營造了不一樣的課堂。數學史為學生提供了探究的機會，為培養核心素養創造了條件;數學史讓課堂變得人性化，充滿文化的芬芳;數學史也為課堂注入了豐富的德育元素。因此，HPM視角下的數學教學有著廣闊的前景，必將成為一種常態。

2在將數學史融入數學教學時，教師需要在創新性和有效性之間尋求平衡。發生教學法強調，要讓學生認識到新知的產生是源于問題解決的需要[10]。透過數學史，我們才能找到知識產生的動因;課堂上運用數學史的重要目的之一在于揭示新知的必要性，激發學生的學習動機。如果學生學會了一個命題的推導，卻不知道該命題從何而來、為何而來，那么他對于命題不可能有深刻的理解，數學史也就失去了應有的意義。這就是為什么說有效性是教師選取數學史材料的重要原則之一。

3教育取向的數學史研究始終是教學實踐的重要基礎，HPM視角下數學教學是否成功與精彩，往往取決于史料本身。本文中兩節課所采用的數學史料均局限于幾何領域，而基本不等式本身所屬代數領域的史料卻付之闕如，有待深入挖掘和整理。

參考文獻：

[1]汪曉勤.HPM：數學史與數學教育[M].北京：科學出版社，2017.

[2]汪曉勤，郭錦融.古希臘數學中的均值不等式[J].中學數學月刊，2015（2）：54-56.

[3]汪曉勤.均值不等式：從歷史到課堂[J].數學傳播，2014（4）：?53-67.

[4]汪曉勤.從“勾股容方”到均值不等式[J].數學通報，2015?（2）：7-9.

[5]關嘉欣.HPM視角下均值不等式的教學設計[J].中學數學研究（華南師范大學版），2017（5）：?32-33.

[6]文靜.行走中欣賞西歐現代建筑之十：維琴察的巨匠：帕拉第奧[J].中國對外貿易，?2013（1）：?88-92.

[7]沈中宇，李霞，汪曉勤.HPM課例評價框架的建構：以“三角形中位線定理”為例[J].教育研究與評論（中學教育教學），2017（1）：35-41.

[8]陳晏蓉，汪曉勤.數學史料的選取原則與案例分析[J].教育研究與評論（中學教育教學），?2017（12）：37-43.

[9]汪曉勤.基于數學史的數學文化內涵課例分析[J].上海課程教學研究，2019?（2）：37-43.

[10]吳駿，汪曉勤.發生教學法：從理論到實踐——以數學教學為例[J].教育理論與實踐，2013?（2）：3-5.