“學會打太極”

顧琴芳

摘 要：“讓學”強調要留足可以供學生探討數學問題的空間與時間，體現了生本化教學的思想。“引思”是在“讓學”前提下對學生數學思考、探究過程的引領、指導與幫助。在“讓學引思”模式下的小學數學課堂，理應將過去提倡的一些有價值的做法整合起來，形成一個辯證的課堂支持系統，幫助學生打造一個有效的探究去向，在協同中闡述新課程理念。

關鍵詞：小學數學；讓學引思；生本化

記得上世紀末筆者剛參加工作的時候，啟發式教學紅遍大江南北，但后來也有不少教師感慨：“如果學生啟而不發，那我們該怎么辦呢？”進入新世紀，隨著“新課程”名稱的出現，“生本化教學”逐漸涌入教師的視線，慢慢地，又有人呼吁：如果把學生捧上天，我們老師還有什么地位呢？再后來，“有效教學”、“思維課堂”、“核心素養”又成為課改的關鍵詞。最近，筆者發現不少地方興起“讓學引思”的熱潮，筆者認為“讓學引思”較全面地反映了師生之間應該有的關系，給教學改革帶來了一片嶄新的天地。

“讓學引思”包括“讓學”與”引思”兩個元素，“讓學”強調的是教師要留足可以供學生思考、探討數學問題的空間與時間，使其有機會學，想學，這體現了生本化教學的思想。“引思”是在“讓學”前提下對學生數學思考、探究過程的引領、指導與幫助，這其實就是實施啟發式教學。結合自己的學習與實踐，以下談談小學數學教學中的“讓學引思”策略，與同行探討。

一、充分考慮課時需要，“讓”得精準才能“促”到本真

課時教學的學習目標為“讓學引思”提出了需求與方向，但是現實中常常出現教學行為與教學目標發生偏離的情況。以計算教學為例，在目前的課堂教學中，對算理的探究仍沒有引起足夠的重視，不少教師還是以僵化的法則教學替代有意義的算理教學，甚至以讓學生背誦口訣為首要任務，嚴重偏離了新課程提出的“讓學生理解與融會貫通”的方向。所以無論是“讓學”還是“引思”，都不能背離課時目標的需求。

由上可見，對于這部分內容的教學，教師如果全盤控制起來，讓學生機械地去識記計算法則，那學生只能淪為計算方法的奴隸，此時教師的“讓學”應著眼于算理，著手于用已有經驗解決新問題情境，再總結出計算法則。顯然這樣的計算法則是經過“醞釀的米酒”，他的本質是“大米淀粉”，也就是算理。

二、及時營造“憤悱”氛圍，“讓”出疑惑才能“引”發深思

曾經何時，老師們喜歡煞費苦心地設計一些動人的情境來吸引學生，尤其在多媒體時代，聲、光、電為課堂提供了足夠的技術支撐，似乎也調動了學生的參與熱情。但這種情境對于教學的影響往往只是一種外部興趣，并沒有真正涉及對問題本質下的熱愛。打個比方：家長給生病的孩子吃藥時會在藥里加糖，此時孩子只是對糖有興趣，一旦糖撤消，那學生會更不肯吃藥——這就是情境教學處理不當所造成的副作用。在“讓學引思”的教學思路下，“讓學”必須指向學習內容本身，引思也應該圍繞教材內容而展開，任何外在的吸引充其量是弱化學生學習興趣的“糖”。

記得在引導學生探究 “3的倍數的特征”的時候，筆者設計了這樣一個訓練序列：第一步，請說說能被2、5整除的數的特征；第二步，觀察下列數字，分析他們能否被3整除，并發現他們的特點：6，36，516，8，38，9，69，33，93，123，423；第三步，.根據上述研究，我們能否得出能被3整除的數的特征？可以發現，這是筆者設計的一個思維陷阱。由于受能被2、5整除的數的特征規律的影響，加上教師刻意安排了一些特殊的數字來讓學生研究，使得有很多學生馬上進入了“圈套”，他們果斷地認定：能被3整除的數的特征是個位數字能被3整除。

師：很好，大家看到了這跟2、5很類似，從而能總結出同樣的規律，那么這樣的總結是否真的正確呢？大家的結論是不是對所有整數都符合呢？

眾生：這……難道……（疑惑不解，思忖著老師是不是又耍了什么花招）

師：我們要推翻剛才所說的規律，只要——

眾生：（接）舉出反面例子。

師：那誰能舉出一個反面例子呢？

生1：老師，15是的，因為15能被3整除，但個位上的5不是3的倍數。

生2：老師，27能被3整除，但個位數7不是3的倍數。

（這時，學生紛紛舉起了手，而且發現能推翻剛才結論的數字很多，開始認定剛才的思考是一種錯誤。）

師：不過，有些數還是可以只看個位上的數字而確定能否被3整除的，有些數就不能，都是哪些數呢？

生3：老師，我發現了象一位數，還有兩位數中“3Δ”、“6Δ”、“9Δ”這樣的數可以。

生4：對，這些數其實就是每一位上的數都能被3整除。

師：好，那么兩位數中如果不符合每一位上的數都能被3整除，那他就一定不是3的倍數嗎？

眾生：好像也不是……

俗話說：“恨之深，愛之切”、“吃一塹，長一智”。在課堂教學中，這種失敗的探究使學生面臨“山窮水盡”的“恨”與不滿之中，經由教師的巧妙引導，學生又能慢慢打開思路，迎來“柳暗花明”。這樣的教學最能讓學生產生心靈的震撼，使興趣、知識與技能在峰回路轉中豁然開朗。由此可見，教師通過“讓學”，使學生得出疑惑，再通過“引思”來化解學生的疑惑，這樣的教學過程充滿了戲劇性，也給課堂帶來了無限的生機。

三、巧于深入層層拓展，“引之有方”才能讓出深度

教材只不過是學生學習知識的一種普遍化工具，“用教材教”的理念為我們開展有效的“讓學”與“引思”提供了一定的底氣。比如對于三角形的面積公式的探究，一般教材只給出利用兩個全等三角形拼成平行四邊形一種方法，但我們盡可以再進行深化：

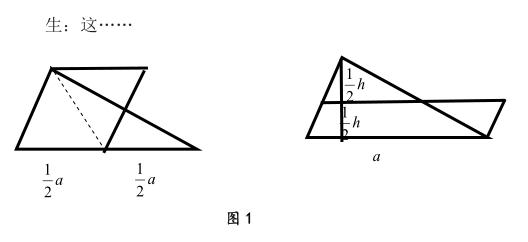
經過上述引思，學生終于發現三角形的面積還可以通過計算底邊的一半再乘高得到，甚至可以先算出高的一半再和底邊相乘得到。具體思路如圖所示，這里三角形的面積不再是“同底等高的平行四邊形面積的一半”這樣的呈現形式，而是等于“高不變條件下取底邊的一半形成的平行四邊形的面積”和“底邊不變條件下取一半高所形成的平行四邊形”，這樣的創新研究也同樣能得到完全正確的答案。通過三種方法的研究，學生對于三角形面積公式的得出變得更為靈活與靈動，知識掌握更為牢固。

在開放的時代，學生的思想都非常活躍，他們的智慧遠不是單一的思路可以框定的，這就需要我們大膽地“讓學”，巧妙的“引思”，才能使知識形成的過程充滿著創新的智慧，充盈著靈氣的光輝。

四、充分尊重學生需求，“引”之靈活更顯“讓”得靈動

課堂是千變萬化的，一旦教師事先決定了該在何處“讓學”，那么教師的“引思”就會圍繞“讓學”的重點而展開，這并不是說教師必須完全按照事先設計來照本宣科，相反，只有隨機應變的“引思”才能使“讓學”變得靈動而有價值。

比如在圓柱體體積的探究過程中，有學生提出：為什么長方體體積是長、寬、高之積，而圓柱體體積卻不是幾條線段長度之積呢？筆者發覺此時學生的疑問帶有普遍性，這正是相互比較進行知識融合的一個極好時機。于是筆者引導道：圓柱體與長方體是不同的物體，但有人發現他們的面積之間有著密切聯系，你認為這種聯系體現在哪兒？此時，有學生發現：其實長方體的體積也可以看成底面積乘高。教師就問他為什么？他說長方體中的長乘寬其實正好是長方體的底面積，所以長方體體積也適用底面積乘高。于是教師又趁熱打鐵：那么長方體體積可以看成三條線段之積，那么這在圓柱體中也成立嗎？于是又有學生發現，原來圓柱體體積可以看成以“半徑×半徑×高×π”，就是某個特殊長方體體積的π倍，是一個怎樣的長方體呢？在教師的引導下，學生紛紛嘗試畫圖，盡管立體圖形繪制的難度較大，但還是有不少學生畫出了這個長方體，從而使長方體與圓柱體的體積之間產生了必然的聯系。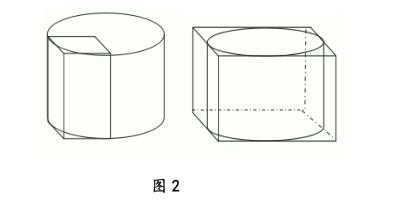

如針對圖2（右）的思考題：在一個底面為正方形的長方體立柱中切出一個最大的圓柱體，那么圓柱體體積與長方體體積之比是 。假如學生對圖2（左）有充足的探究，那么不但能理解圓柱體體積與對應長方體之間的關系，還能很快找到解題思路：設圖2（左）中長方體的體積為X，那么對應的大圓柱體體積為πX，對應的圖2（右）中的大長方體體積為4X，所以這道題的答案應為π：4。顯然，教師在教學中的充分“讓學”，體現在“引思”過程中的不拘一格，讓學生實現“條條道路通羅馬”，從而可以以最優方案來解決特殊的問題。

由上可見，“讓學”與“引思”正像打太極拳時的兩只手，兩手同時環抱一個氣團，一手拎時另一手托，一手跑時另一手追，一手回時另一手相應地退，兩手互相配合，協同作戰。“讓學”與“引思”是一對矛盾，在不斷碰撞中走向成熟，達成和諧。在“讓學引思”模式下的小學數學課堂，理應將過去提倡的一些有價值的做法整合起來，形成一個有效的探究去向，在協同中闡述新課程理念，既實現有效的啟發式教學，也達成有價值的生本化教學，最終實現核心素養的提升。

參考文獻

[1]“提問”——讓課堂更精彩[J].孫乃群. 小學教學參考.2012（05）

[2]淺談素質教育課堂教學和評價[J].梅友榮，施大瑜. 小學教學參考.2006（18）

[3]李芳.讓學促思開拓教學新視角[J].基礎教育研究，2016，（23）