《用字母表示數》教學實踐及思考
梁勤
【摘要】本文以《用字母表示數》的教學為例,論述在教學實踐中給學生提供三個關鍵體驗點,即體驗數的確定與不確定,體驗同一件事件與不同對象,體驗兩個量之間的關系及應用,并整合“三個體驗”之間的關系,促進學生理解用字母表示數的抽象知識,提升數學邏輯思維能力。
【關鍵詞】《用字母表示數》 教學實踐 思考
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2021)33-0112-02
“數”和“數字”是比較抽象的概念。教師在教學中常常分不清楚什么是數,什么是數字,通常會認為數就是無數個數字,而數字只有10個,即0,1,2…9。關于物的個數屬性,人腦通常會用抽象圖來表示,再將圖表示成具體的數字。在一年級小學數學教學中,學生用數字來表示數,這個時候學習的數是確定的,進入高年級階段則出現了一些無法確定的數,這些數具有多種可能性。為了表示數的多種可能性,就可以用字母來表示。現以人教版數學五年級上冊《用字母表示數》這一課的教學為例,談談課堂教學體驗活動的設計,幫助學生理解什么時候需要用字母表示數,什么時候不需要用字母表示數。要實現對這一知識的理解,教師需要給學生提供三個關鍵的體驗點,并注意整合三個體驗點之間的關系。
一、體驗數的“確定”與“不確定”
在小學數學教學中,數學體驗活動就是讓學生親歷特定的數學活動,感受和發現數學問題,領悟數學思想方法,由此產生積極的情感體驗和內省反思,學生借助體驗活動,經歷數學概念的形成過程,獲得感知、領悟和概念建構,從而發展數學能力。為了讓學生完整體驗什么是“確定的數”、什么是“不確定的數”,筆者選用一個信封和一盒鉛筆展開教學。
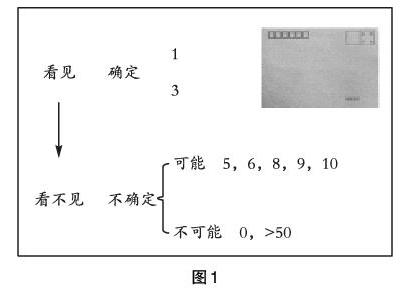
筆者先讓學生觀察信封,提問:信封里沒有任何東西,這個時候可以用什么數來表示呢?學生認為可以用數字“0”來表示。筆者又往信封里放進1支粉筆,引導學生思考:現在可以用什么數來表示呢?學生認為可以用“1”來表示,因為這“1”支粉筆是確定的。接著,筆者將這1支粉筆抽出來,再在信封里放進3支粉筆,讓學生觀察并說出可以用什么數來表示。學生可以實實在在地看見這3支粉筆,認為可以用數字“3”來表示,因為這個數字是確定的。緊接著,筆者把信封放在學生看不到的地方,告訴學生信封里面已經放了粉筆,再讓學生想一想:信封里的粉筆可以用什么數來表示?學生只能猜想信封里的粉筆可能有5支,或7支,或10支等。筆者提問學生:為什么現在信封里的粉筆數是“可能”的呢?學生認為,看不見教師裝了多少支粉筆,所以不確定數量。筆者將裝了粉筆的信封拿出來,追問學生:現在大家不確定這里的數是幾,但可以確定哪些數是沒有的呢?請你舉例說一說。學生認為這個信封是鼓著的,所以可以確定數字“0”是沒有的;這個信封最多不能超過50支粉筆,因此可以確定“50”這個數也是沒有的。筆者引導學生再次梳理整個體驗過程。(如圖1)
學生通過體驗,認識到了數的“確定”和“不確定”之間的關系,并能夠從“不確定是幾,但能確定不是幾”這個體驗過程,認識到了不確定的數可以選用字母來表示,如字母a等,并認識到了這個字母代表的區間范圍。由此,借助用字母表示數的體驗過程,讓學生在以后學習列方程解決實際問題時,對假設“誰為x”就有了深刻的理解和體會。
二、體驗“同一事件”與“不同對象”
用字母表示數具有兩個范疇的體驗層次,即一元性與多元性,其一是用字母表示數來解決“一元”的問題,其二是用字母來表示數解決“多元”的問題,這就需要教師引導學生經歷用字母表示數的多元體驗過程,體驗在同一件事中針對不同的對象運用不同的字母來表示。對此,筆者設計了以下教學環節。
以學生熟悉的頭發為例,先讓男生指出自己的頭發有多少根,用什么字母來表示,再讓女生指出自己的頭發有多少根,用什么字母來表示。學生認為,男生的頭發數可以用a來表示,而女生的頭發數比男生的頭發數多一些,所以女生的頭發數用字母b來表示。經過這樣的討論,學生認可了用不同的字母可以表示不同的兩個對象。
緊接著,筆者以信封和粉筆作為素材,拿出了第2個信封。筆者在學生看不見的地方把粉筆裝進信封,并提問學生:信封里有多少根粉筆?學生指出可以用a表示,也可以用除了a之外的任何字母來表示。
通過以上教學環節,學生由此體驗到了同一件事里,不同的對象可以用不同的字母來表示。
三、體驗“兩個量”的關系及應用
筆者給學生出示兩個信封中的粉筆數a和b(如圖2),引導學生思考:第1個信封中的粉筆數用a表示,第2個信封中的粉筆數用b表示,這兩個數如何比較?學生認為這兩個數都不確定,所以無法比較。筆者追問:這個“不確定”會有幾種可能性?學生指出有三種可能,即a大于b,或者a小于b,或者a等于b。
筆者又以聽課為例,引導學生思考:今天來聽課的人大約有多少人?學生指出有a人。追問:來聽課的學生有多少人?學生數了數,一共有34個人。學生繼續思考:今天來聽課的大人有多少人?有b人。緊接著,筆者引導學生比較a和b的大小,學生經過討論認為:a>b。
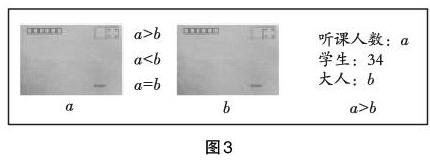
筆者向學生出示前后兩次字母a與b的大小比較過程(如圖3),讓學生觀察并思考:為什么同樣是比較a與b的大小,同學們卻得出不同的答案?
學生認為,左邊兩個信封中的a與b并不能夠確定是什么關系,右邊的a與b是總數和部分的關系。
筆者引導學生繼續展開討論:會場中人數是a,學生有34人,大人的人數是b。這里的a比b大,大多少呢?學生認為,a比b多出來的人數正是小朋友的人數,即34。筆者追問:如果大人的人數不用字母b表示,還可以用什么表示呢?學生展開討論,有的認為可以用c或者d表示,還有的認為可以用字母式“a-34”表示。筆者追問:用b表示和用“a-34”這個字母式表示,哪一種表示方法更直接?學生經過討論認為,當兩個量有關系時,其中的一個量用字母式表示更直接、更好。
通過以上體驗環節,學生感受到了兩個量之間的關系,能夠運用字母表示未知數進行兩個量之間的比較,在此基礎上,還可以將字母作為已知數參與其中,體驗并建立字母式。
四、整合“三個體驗”之間的關系
在以上體驗數的確定與不確定、體驗同一事件與不同對象、體驗三個量之間的關系與應用中,學生獲得了三種理解,這三者存在著完整的關系。這需要教師對這三個關系進行整合和反思,幫助學生建構用字母表示數的數學本質。為此,筆者以池塘中的青蛙為例引導學生展開梳理,先讓學生思考:1只青蛙1張嘴,2只眼睛4條腿,如果用字母表示池塘中的青蛙,應該怎么表示呢?學生認為,池塘中的青蛙到底有多少只我們并不知道,因此可以用字母a來表示,就是“a只青蛙a張嘴,a只眼睛a條腿”。這是基于第一個體驗點獲得的理解,將不確定的數用字母表示。
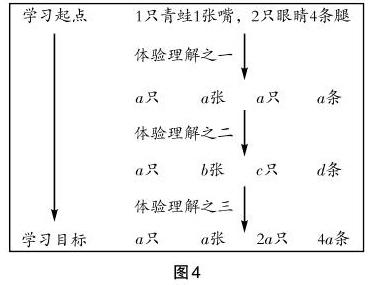
基于第二個體驗點的理解,將不同的對象用不同的字母來表示,學生認為可以用“a只青蛙b張嘴,c只眼睛d條腿”來表示;再基于第三個體驗點的理解,基于對象之間的關系用字母式表示數,學生用“一只青蛙一張嘴,2a只眼睛4a條腿”來表示。筆者向學生展示整個體驗過程(如圖4),帶領學生進行概念的整合和建構。
在以上環節中,學生以用數字表示數作為出發點,達到用字母表示數這一目標,經歷了對三個體驗層次的理解,從而實現了學生對數學概念的本質理解。在這三個體驗環節中,學生一步步梳理其中完整的邏輯關系,慢慢地感悟到了用字母表示數在教學實踐中的重要作用。
綜上所述,筆者摒棄了以往教學中對知識的復制和灌輸的教法,將學生放置在具體的活動體驗過程中,讓學生從自己已有的知識和經驗出發,自主感受、理解、建構,從而提升數學邏輯思維能力,建構起用字母表示數的抽象知識系統。
【參考文獻】
[1]匡艷.探討小學數學教學中培養學生高階思維能力的策略[J].數學學習與研究,2020(20).
[2]馬紅艷.經驗:小學數學教學的重要載體[J].小學教學參考,2013(8).
[3]徐鋒,楊曉榮.數學基本活動經驗積累的六個“著力點”[J].江蘇教育研究,2014(29).
【作者簡介】梁 勤(1978— ),女,廣西玉林人,大學本科學歷,一級教師,現就職于玉林市福綿區福綿鎮沙浪小學,研究方向為小學數學教學。
(責編 楊 春)

