基于數學歷史的勾股定理教學設計

李織蘭 肖寶瑩 沈潔 蔣曉云

【摘要】本文在解讀課標和分析教材及有關勾股定理教學文獻的基礎上，闡述勾股定理教學設計，即以歷史故事為引子，帶領學生初識勾股定理，讓學生通過實驗歸納發現勾股定理，并了解“出入相補，無字證明”的方法，以培養學生科學精神和數學核心素養。

【關鍵詞】勾股定理 科學精神 數學歷史 核心素養

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2021）33-0149-04

勾股定理是數學發展史上一顆璀璨的明珠，只要說到勾股定理，我們總會想到“商高”“勾三股四弦五”“畢達哥拉斯”“趙爽弦圖”“出入相補”等，在勾股定理的研究歷程中彰顯了古今中外研究者的數學精神。其證明方法也極其多樣化，體現了各國數學家孜孜不倦的鉆研精神。勾股定理是數學發展的重要根基之一，它不僅被認為是平面幾何中最重要的定理之一，也被認為是數學中最重要的定理之一。勾股定理是初中數學課程的核心內容之一，歷來是教學改革的風向標。

一、課標解讀與教材分析

《義務教育數學課程標準（2011年版）》強調了數學文化在課程中的價值，指出在人類文化中數學文化占據著重要位置，并要求在數學課程的教學中適當融入數學文化。

勾股定理用中文表達是，直角三角形的斜邊的平方等兩直角邊的平方和;用數學語言來表達是，如果直角三角形的兩直角邊分別為a和b，斜邊為c，那么c2=a2+b2。

它揭示了直角三角形三邊之間的數量關系，體現了數形結合的思想方法。勾股定理啟發了人類對數學的深入思考，促成了三角學、解析幾何學的建立，為數學的進一步發展拓寬了道路。因此，勾股定理和黃金分割被譽為“幾何雙寶”，前者好似珠玉，后者堪稱黃金。本節課選自人教版初中數學八年級下冊第18章第1節《勾股定理》的內容。課文以發現和證明勾股定理的各種幾何方法為主線。在此基礎上，我們梳理了發現和證明勾股定理的歷史過程，從而決定以勾股定理發展的歷史文化背景為暗線。在這兩條線上設計課堂教學過程，并將兩條線貫穿整堂課的始終。目的是借助勾股定理豐富的文化背景，培養學生科學精神。幾千年來，在勾股定理探索的過程中，一代代人皓首窮經，不斷積累，才挖掘出數學中的這一珍寶。數學大師們在生活中發現和思考，不懈地探索，找到了一個個精妙的解決直角三角形的方法，并將勾股定理的發現和思想方法推向一個又一個新領域。它擁有無窮的奧秘，亟待我們去探索、去追尋。我們要學習數學家刻苦鉆研的精神，不斷探索數學的奧秘。在課堂上，我們可以沿著大師的足跡，經歷發現勾股定理的過程，運用實驗歸納方法體驗從特殊到一般的歸納思想。在教學中，教師也可適當講解數學界有關給勾股定理命名的歷史。勾股定理的命名是一件令中華民族深感無奈和遺憾的事情。從這件事情上讓學生思考，發現一個規律，或解決一個問題之后，去追求“更普遍的真理”“更一般的規律”是何等的重要。要培養良好習慣，具備科學的思維品質，培養數學精神。

我國古代數學趙爽用弦圖證明勾股定理，是一種數形結合證法，它建立在一種不證自明、形象直觀的原理上。他在證明過程中，借助圖形使問題數學化。在課堂上，教師可介紹這種方法，讓學生了解勾股定理的這一種證明過程，學會用“出入相補”的證明方法，體會數形結合思想。弘揚中國古代數學家輝煌成就，感悟古人的智慧，增強民族自豪感，培養愛國主義精神。

二、勾股定理教學文獻分析

在CNKI按檢索式“發表時間between（2016-04-01，2021-04-01）and主題=勾股定理教學”進行檢索，檢索到文獻共161篇，從發文量可看出，勾股定理的教學研究是近年的研究熱點問題之一。

為了借鑒優秀教學成果，通過對文獻整理，從勾股定理的發現教學和勾股定理的證明教學這兩個方面進行了教學分析。

（一）發現勾股定理的教學

多數文獻是通過畢達哥拉斯參加聚會的故事，引導學生了解從探究等腰直角三角形，推廣到一般的直角三角形，從而得到直角三角形三邊之間的數量關系的研究方法。筆者主要參考以下幾個人的文獻：（1）郝金芝的文獻，通過提問學生“如果兩個特殊條件——‘等腰、直角’缺少其中一個條件，那么三角形還具有這樣的性質嗎？”添加條件或去掉條件，得到三個不同條件的直角三角形，再根據探究等腰直角三角形經驗找到解決問題的方法。啟發學生利用網格內正方形面積的方法進行探索，通過辨析、猜想、發現，最后得出結論。在這一過程中，通過添加或去掉條件進行研究，進而找到共性的這個過程很新穎，體現特殊到一般的歸納思想。（2）盧明一、張新然、曾澤群等人的文獻，在講述了畢達哥拉斯故事后，引導學生通過研究面積關系，并將之轉化為三邊關系，從而發現等腰直角三角形的性質。在此基礎上，探究普通直角三角形的性質。利用正方形面積的關系，利用割補的方法求出以直角三角形的斜邊為邊建立正方形，得到的面積與兩直角邊對應的正文形的面積的關系，從而發現直角三角形的三邊的關系——勾股定理。這個過程是一個探究式的學習過程，讓學生體驗從特殊到一般的過程。在這個過程中，培養學生歸納的思想，體現數學史的教育價值。

（二）證明勾股定理的教學

證明勾股定理的方法很多，絕大多數教學研究文獻通過滲透數學史、融入數學文化等途徑，讓學生了解勾股定理的證明過程，循大師足跡，悟數學文化，培養數學精神。筆者主要參考以下幾個人的文獻：（1）郝金芝，引導學生將任意的直角三角形放入網格中，觀察頂點是否在格點上。如果在，那么就可利用三邊的特殊性求解三邊的關系;若不在，那么應該怎么去求三邊之間的關系？讓學生借鑒之前利用網格發現勾股定理的研究思路，通過圖形拼接，進行一般性證明。（2）趙爽，利用弦圖法，對圖形進行拼、割，然后利用面積法證明。這個證明過程比較嚴謹，值得學習。這些文獻資料闡述的證明勾股定理的方法，比較注重數學史的傳承問題，旨在使讀者感受古人的智慧。（3）盧明一，向學生講述趙爽弦圖的方法，通過幻燈片將整個拼擺過程動態地展現，讓學生直觀地看到證法的整個過程。然后利用幾何畫板演示直角三角形，改變三邊長度，發現其三邊關系保持不變，從而證實勾股定理。在這整個過程中，讓學生動手實踐，觀看利用趙爽弦圖證明勾股定理的視頻，然后利用信息技術對證明過程進行驗證。這樣既能加深對勾股定理的理解，又能體會我國古人智慧，讓學生感受數學文化。（4）張新然，以四個全等的直角三角形為研究對象，讓學生動手拼擺，當擺到與趙爽弦圖一樣時，再利用幾何畫板為學生演示。這種教學活動可培養學生動手能力，感受數形結合思想。

這些文獻的教學設想和方法值得我們借鑒，而如何充分發揮勾股定理的文化價值和教育價值仍需進一步思考。

三、基于數學歷史的勾股定理教學設計

在教學中，教師基于自身的教學視野、數學理解能力、數學史功底，精心教學設計，讓學生沿著歷代數學大師的足跡，復現數學大師的思維過程，使之得到啟迪;進而使學生能夠根據自己的體驗，用自己的思維方式，“再創造”數學，形成科學精神。結合教材內容和教學目標，筆者安排本課的教學流程如下：

（一）歷史故事，初識定理

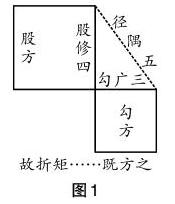
在我國古代，人們將直角三角形中短的直角邊叫做勾，長的直角邊叫做股，斜邊叫做弦。3000多年前，中國古代人們已經知道，如果勾是三，股是四，那么弦是五（如圖1所示）。這是商高發現的經過后人進一步證明了的勾股定理中的一個特殊例子，但特例以外還有無窮個直角三角形不能用“勾三股四弦五”來求解。

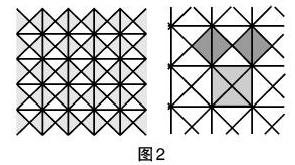
相傳2500年前，有一次，畢達哥拉斯到朋友家中做客，他在欣賞鑲嵌在地面上美麗的地磚時，發現它們和“數”之間的關系：兩個小正方形的面積的和等于這個大邊長正方形的面積，這是等腰直角三角形的一個性質（如圖2所示）。畢達哥拉斯發現等腰直角三角形的這一特殊性質之后，他還研究了很多不同類型的直角三角形，歸納發現：任意直角三角形兩直角邊的平方和等于斜邊的平方。讓學生跟隨畢達哥拉斯的腳步，一起來做實驗，探究一般的直角三角形的三邊數量關系。

【設計意圖】介紹勾股定理的歷史起點，并將之當作本節課暗線的起點。借助教材的章前圖文激發學生的學習興趣。讓學生體悟從特殊到一般的研究問題的思想。

（二）實驗歸納，發現定理

畢達哥拉斯發現等腰直角三角形這一特殊性之后，他繼續思考：對一般直角三角形是不是也存在這樣的“三邊”的數量關系呢？

三個正方形的面積，實際也分別是對應直角三角形的三條邊的平方，從而獲得一個關于直角三角形性質的初步結論：兩直角邊的平方和等于斜邊的平方。從特殊的現象中提出問題。

學生活動1：在方格紙上畫出任意直角三角形，分別以三邊向外作三個正方形，通過割或補的方法計算各正方形的面積，驗證三邊的平方關系。（如圖3所示）

【設計意圖】此時直接讓學生去證明三邊的平方關系，難度很大，為了降低學生的思考難度，教師及時引導，回到課堂開始的圖形，直接提示學生借助方格紙作圖，利用面積的割或者補的方法得到邊長的平方關系。以此打開教學，突破難點。

學生在網絡方格紙上獨立畫直角三角形，并利用網絡方格驗證直角三角形三邊的平方關系。絕大部分同學都能以直角三角形的三邊分別向外作了三個正方形，通過計算正方形的面積來驗證三邊的平方關系。這個過程涉及求方格紙中斜放的正方形的面積問題，這是難點。請兩位同學展示他們不同的驗證方法。

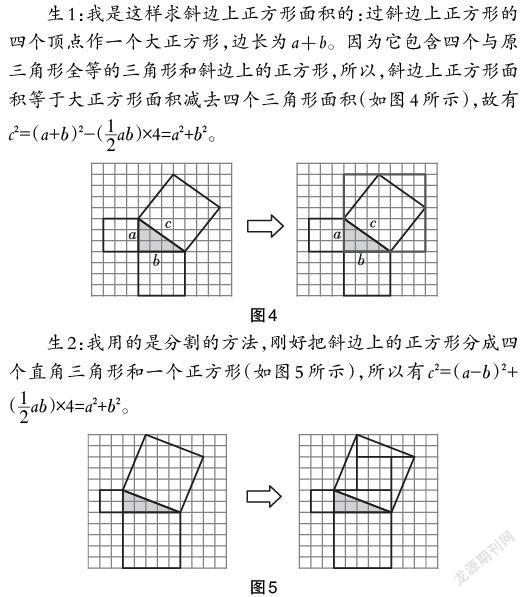
生1：我是這樣求斜邊上正方形面積的：過斜邊上正方形的四個頂點作一個大正方形，邊長為a+b。因為它包含四個與原三角形全等的三角形和斜邊上的正方形，所以，斜邊上正方形面積等于大正方形面積減去四個三角形面積（如圖4所示），故有c 2=（a+b）2-（[12]a b）[×]4=a2+b2。

生2：我用的是分割的方法，剛好把斜邊上的正方形分成四個直角三角形和一個正方形（如圖5所示），所以有c 2=（a-b）2+（[12]a b）[×]4=a2+b2。

師：無論是“割”還是“補”的方法，都是用不同的方法把同一個正方形表示，這種構造法是證明問題的一種思路。

追問1：我們在方格紙中任意作的一個頂點在格點上的直角三角形，都能驗證兩直角邊的平方和等于斜邊的平方，但我們能不能說，對所有的直角三角形，三邊都滿足這樣的關系？

追問2：如果我們把方格紙去掉，會對他們的證明有實質的影響嗎？

實驗驗證還不能算嚴格的證明，因為方格紙具有特殊性，實驗歸納得到的結論可能是正確的，也可能是錯誤的。想要獲得一般性的結論，需要在一般的平面上對一般的直角三角形進行證明。

【設計意圖】讓學生在方格紙上作圖以進一步驗證結果，即用割或者補的方法驗證兩個小正方形的面積之和等于大正方形的面積。在此過程中，讓學生進一步感知猜想的正確性，鞏固常用的割或補求面積的方法，從而使學生體會從特殊到一般的思想，思考并理解怎樣才能使問題一般化;理解把一個問題一般化的方式——用字母表示數，理解通過代數式的化簡得到一般的結論的過程。在不斷追問中使學生初步感受構造法是數學證明的一種思路，為趙爽弦圖證明勾股定理作鋪墊。

（三）出入相補，無字證明

數學以其嚴謹、嚴密、客觀，使人們對其敬畏和信任。數學是求真的，它不輕信實驗、觀察、歸納。在實踐中發現的數學結論必須經受極為嚴格的邏輯檢驗（即數學證明），才能成為定理。

約在222年趙爽創作了一篇“勾股圓方圓說”論文，他畫了一張“弦圖”表述勾股定理，并給出了一個絕妙的證明：“勾股各自乘，并之為弦實，開方除之即弦。案：弦圖又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實。”（如圖6所示）

趙爽弦圖的證明思路：每一個直角三角形稱為“朱實”，中間的一個正方形稱為“中黃實”，以弦為邊的大正方形叫做“弦實”。

趙爽將“勾股定理”一般化才形成了真正的勾股定理，其證明過程有圖為證，永載史冊。趙爽證明勾股定理的這個方法可謂精妙絕倫，為將代數和幾何緊密結合，使之互不可分的一個典范，這個無字證明（不用數學語言證明，如圖7）的方法被哈佛大學教授庫里奇稱為“最省力的證明”。正因為此，“趙爽弦圖”被選為2002年國際數學家大會會徽，現在這個標志也成了中國數學會的標志。（如圖8所示）

劉徽為《九章算術》勾股數——“勾股各自乘，并而開方除之，即弦”所作的注：“勾自乘為朱方，股自乘為青方，令出入相補，各從其類，因就其余不動也，合成弦方之冪，開方除之，即弦也。”

如何將勾方與股方出入相補成弦方？教師進一步介紹數學家劉徽的“青朱出入圖”。（如圖9所示）

劉徽把“趙爽弦圖”和“青朱出入圖”所蘊含的思想方法總結為“出入相補”原理。“青朱出入圖”巧妙地利用了“出入相補”原理，且蘊含動態思想，具有科學創新的意義。

【設計意圖】介紹中國古代數學家證明勾股定理的方法——趙爽弦圖法，使學生了解我國古代數學家對探索勾股定理作出的貢獻，知道他們是我國古代數學的驕傲。感悟古人的智慧，增強民族自豪感，培養愛國主義精神。介紹勾股定理發展的一個歷史線，回看古人數學成就，彰顯古今中外數學精神，培養學生的良好習慣和思維品質，培養學生的數學精神。

（四）數學文化，科學精神

公元前3000年，古巴比倫人就知道了很多組的勾股數，而且留下了實物證據——記滿勾股數的泥板。商高“勾三股四弦五”比畢達哥拉斯發現勾股定理至少要早500年，因此，一些過去的教科書中講是中國人商高最早提出了這個定理，于是稱之為勾股定理或者是商高定理。但課文說：“在西方，一般認為這個定理由畢達哥拉斯發現的。”這是為什么？

古代巴比倫的數學泥板書沒有形成數學理論，泥板書上的數學也因帶有推測的成分故而存在爭議。《周髀算經》中的“勾三股四弦五”只是記載了一組勾股數，是后人進一步證明了的定理中的一個特殊例子，并不能說明發現了任意直角三角形三邊的數量關系的規律，特例以外還有無窮個直角三角形不能用“勾三股四弦五”來求解。一個結論要成為定理，需要做出一個一般性的描述。這個描述可以把它稱為命題，命題經過嚴格的邏輯檢驗（數學證明）才能成為定理。反思中國古代數學家沒有去探究“更一般的規律”，因此幾千年來，西方國家一直稱“直角三角形兩直角邊的平方之和等于斜邊的平方”這一定理為“畢達哥拉斯定理”而不是“商高定理”或“勾股定理”。盡管2002年在北京召開的世界數學家大會把證明勾股定理的趙爽弦圖設計成會徽懸掛在會場，以彰顯中國古代數學家在探索勾股定理的過程中的獨特貢獻和地位，但國際數學界仍然把勾股定理命名為“畢達哥拉斯定理”，勾股定理的命名成了一件令中華民族深感無奈和遺憾的事情。在教學中，教師可通過這件事情讓學生懂得：發現一個規律或解決一個問題之后去追求“更普遍的真理”“更一般的規律”是何等的重要，因此要養成良好習慣，要有科學的思維品質，培養數學精神。

【設計意圖】使學生充分地感受整個數學的發展史就是人類物質文明和精神文明的發展史。求真是數學教育的最高境界，是我們的追求。數學文化綿延古今，經久不息，我們要傳承數學精神。

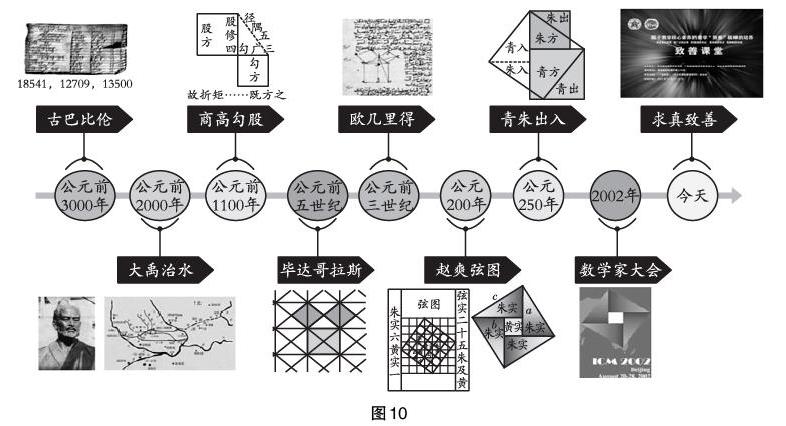
勾股定理是初中數學課程的核心內容之一，歷來是教學改革的風向標。勾股定理的研究過程彰顯了古今中外研究者的數學精神。本課例選自人教版初中數學《勾股定理》的內容，以發現和證明勾股定理的各種幾何方法為主線，梳理勾股定理發展的歷史線;以勾股定理發展的歷史文化背景為暗線，并將之貫穿整堂課的始終（如圖10所示）。在教學過程中，利用勾股定理豐富的文化背景，培養學生科學精神。

【參考文獻】

[1]蔣曉云.文化視角下的小學數學課例研究[J].廣西教育，2018（1）.

[2]郝金芝.“勾股定理”教學設計[J].中國數學教育，2020（11）.

[3]盧明一，李碧榮.基于數學史的勾股定理教學設計[J].廣西教育，2019（29）.

[4]張新然.“勾股定理”教學設計及兩點思考[J].中國數學教育，2019（Z3）.

[5]曾澤群，賴寶禧.HPM視角下的“勾股定理”教學設計[J].數學教學，2019（9）.

[6]張冬莉，代欽.畢達哥拉斯定理證明2500年的文化史趣談——以E.S.Loomis的《Pythagorean Proposition》為例[J].數學通報，2020，59（2）.

[7]俞求是.《周髀算經》“周公商高問答”相關問題的研究[J].數學通報，2019，58（2）.

注：2020年度廣西基礎教育改革發展研究中心課題：基于核心素養的數學“致善”精神的培養策略研究（課題編號GSJJB202005）;廣西教育科學“十三五”規劃2019年度重點課題：小學數學教學中學生“科學精神”的培育研究（課題編號2019B141）。通訊作者：蔣曉云。

（責編 李 唐）