基于兒童“學力生長”的小學數學教學問題鏈設計研究與實踐

楊麗芳

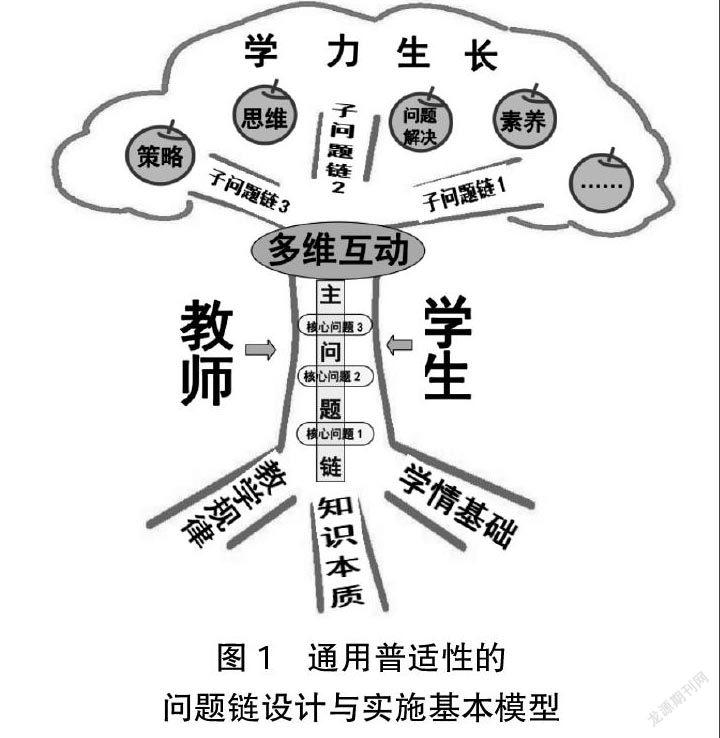
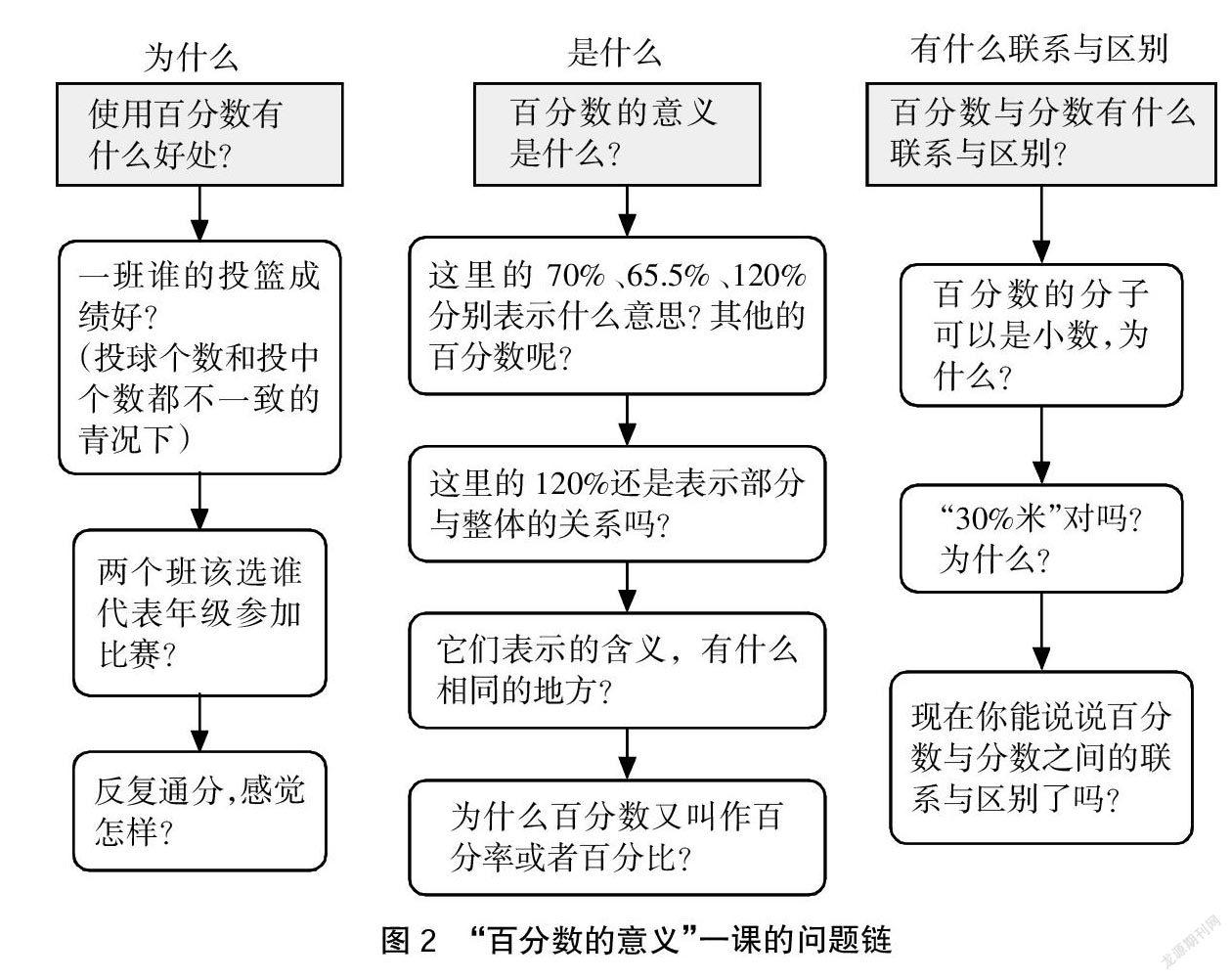
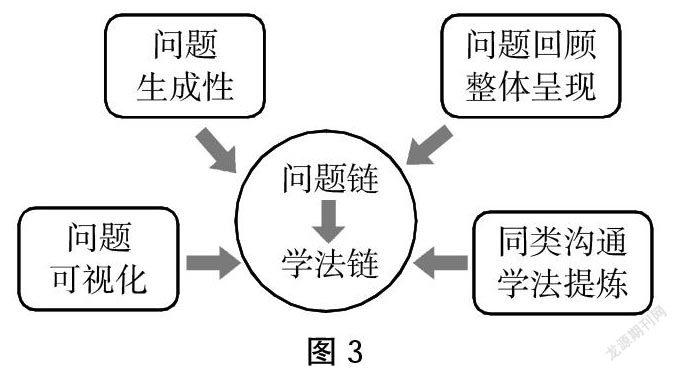
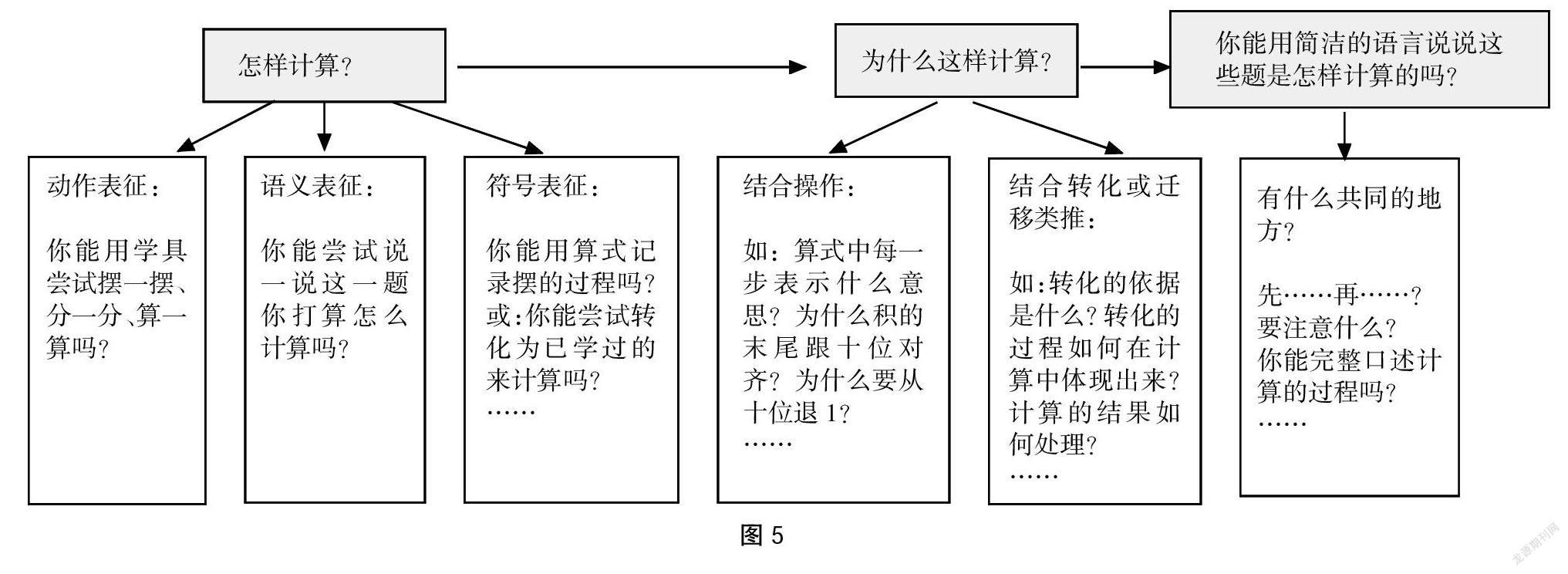
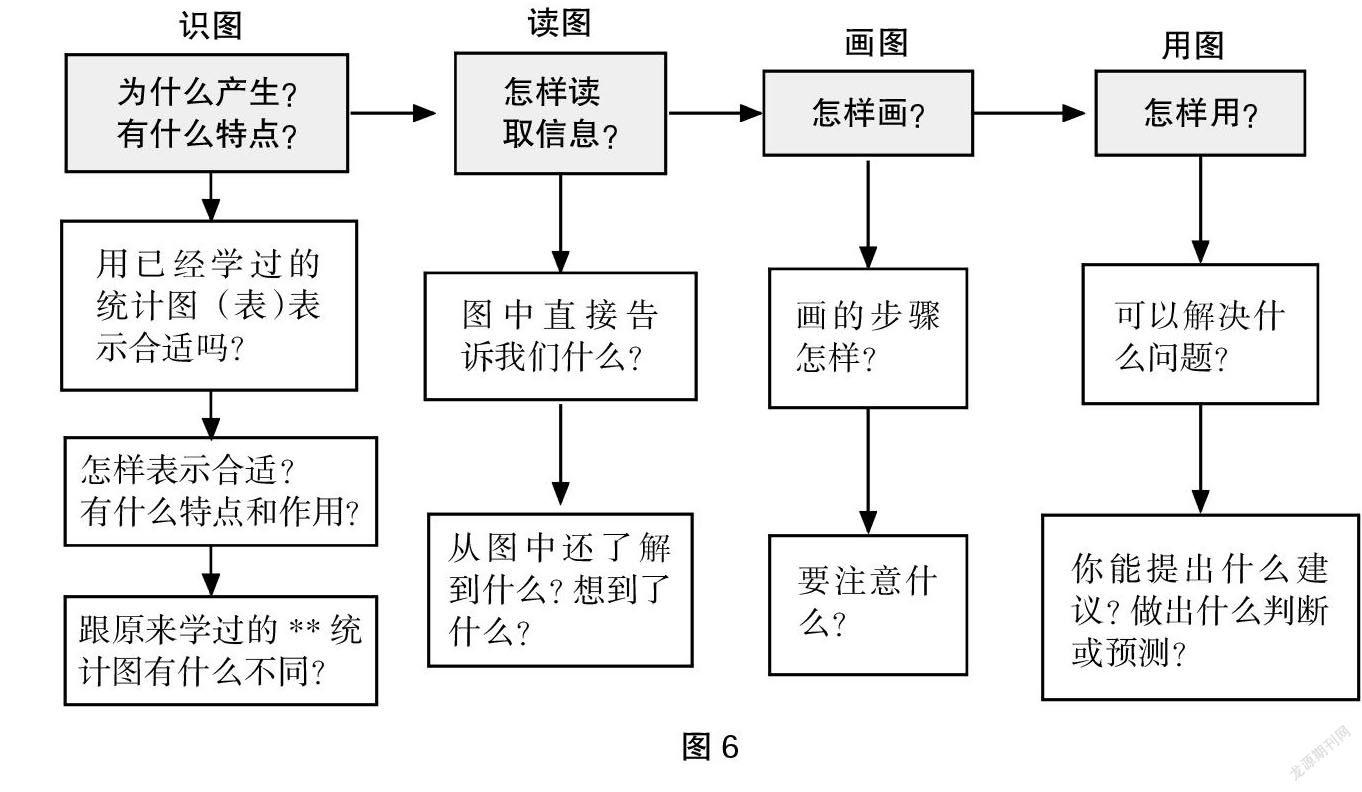
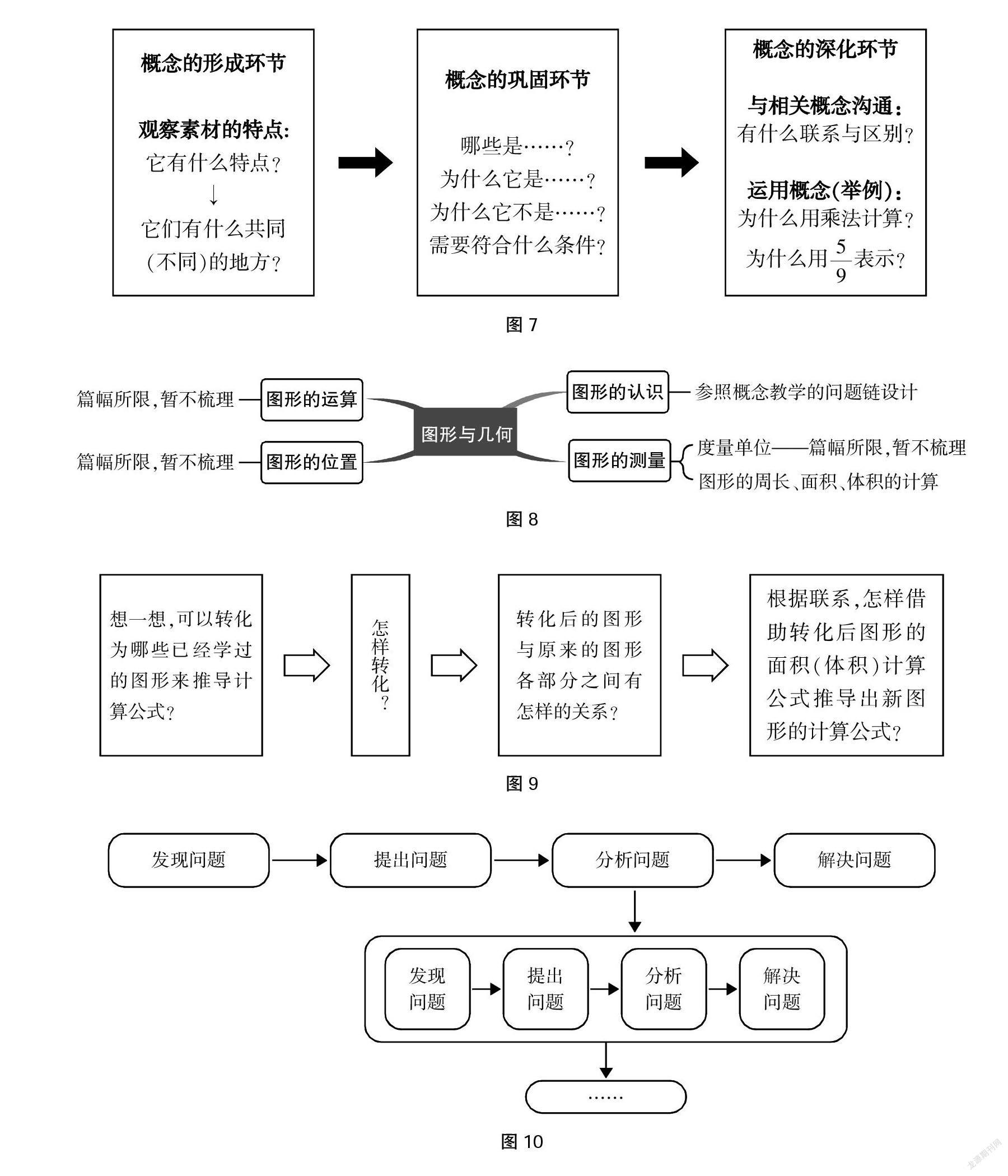
[摘? 要] 兒童的“學力生長”需要探尋可行的技術路徑。一組具有啟發性、 邏輯性、層次性的問題鏈，能助力學生在數學學習中的主動和意義建構，是促進兒童“學力生長”的問題型學力支架。本研究構建了具有通用普適性的問題鏈設計與實施的基本模型，并基于不同類型教學內容的教學規律，把基本模型細化成六種主要課型的問題鏈變式，如解決問題教學、概念教學、計算教學等，為教師的教學問題設計提供了重要參考工具;探索出“問題鏈→學法鏈”“問題鏈→思維活動鏈”的轉化策略，為促進兒童的深度學習、提升學力找到了一條可行的技術路徑。

[關鍵詞] 小學數學;學力生長;問題鏈;基本模型;課型變式

“數學學力”亦被稱為數學能力、數學素養等，是一個發展中的概念。不同的學者在不同的時期對其有不同的理解，但也逐漸形成了一些共識，如強調問題解決和數學思考、核心素養導向、指向高階思維、關注學習策略和學習品格等。

兒童的“學力生長”需要探尋可行的技術路徑。一個良好的問題情境，一組具有啟發性、邏輯性、層次性的問題鏈，能助力兒童在數學學習中的主動和意義建構，發展他們的問題解決能力和培養高階思維，這是促進兒童“學力生長”的問題型學力支架。

一、問題的提出

筆者作為區的教研員，長期到一線進行教學調研，在大量的聽課、評課中發現有相當一部分的教師課堂問題設計的水平低下，其他區域的教研員也反映了同樣的情況。主要存在以下問題。

（一）問題設計欠缺啟發性和深度，思維沒能真正發生，無從談“學力生長”

有部分教師變“滿堂灌”為“滿堂問”，提問隨意，不重視問題設計，沒有掌握一定的問題設計的技巧和方法，對教材又缺乏鉆研。態度和專業水平的缺位造成淺層的問題充斥課堂，問題思維含量低，學生的“學力生長”無從談起。

（二）問題設計欠整體考量，結構零散不成支架，學生的“學力生長”缺乏有效深入的路徑

設計的問題細、碎，局限在某個知識點的分解上，很少從整體性、邏輯性和層次性的角度去設計和評價課堂問題，不能較好地發揮提問的整體功能。學生埋沒在細碎的問題中，不清楚問題解決的總體思路和方向，造成學生的思維生長缺乏有效深入的路徑。

另外不少教師習慣了以課論課，沒有從課型教學規律的高度來把握問題設計的技巧，也就不能實現由一節課到一類課的提升，由此影響了問題設計的科學性和問題設計的效率及質量，同時也影響了學生對某一類學習內容的規律性把握。

（三）問題設計重教不重學，缺乏把“問題鏈”轉化為“思維活動鏈”和“學法鏈”的有效策略

即使相對優秀的教師，往往都只是把問題鏈定位為教的工具，較少設計有效的實施策略去促進學生思維的深度參與，也沒有認識到“問題鏈”實則就是學習方法提煉與遷移的“學法鏈”，它能幫助學生實現從一節課到一類課的提升。教師的認識不到位使問題鏈更多停留在教的層面，未能把“問題鏈”轉化為學生的“思維活動鏈”和“學法鏈”。

綜上，教師觀念、態度和專業水平的缺位，造成問題設計水平的低下，學生的“學力生長”缺乏有效深入的路徑，因而十分需要開展本項目的研究，有針對性地解決當前教學中存在的問題。

二、解決問題的方法

圍繞兒童的“學力生長”，筆者從教與學、設計與實施兩方面開展研究，歷經8年的實踐與檢驗，構建了問題鏈設計與實施的基本模型，探索出“問題鏈”向學生“思維活動鏈”和“學法鏈”轉化的有效策略，搭建了基于課型特點的六種主要課型問題鏈支架。

（一）構建了一個基本模型

1. 模型的構建

筆者遵循先通用，后變式，教與學雙向融合共同推進的研究思路，開展問題鏈的設計與實施的研究，構建出通用普適性的問題鏈設計與實施的基本模型，具體如圖1所示。

2. 模型的解讀

（1）根深才能葉茂——深挖本質，夯實問題鏈設計基礎

設計一節課的問題鏈，我們不能只關注知識的表面形態，而要側重于其內核與實質的分析。數學知識的本質、教學的規律以及學生的學情這三者是問題鏈設計所要依托的數學教學的本質。因此設計問題鏈時，需要把握好明、暗兩條線，明線是指教材的具體內容編排以及學生的學情基礎，暗線是指對數學知識本質的理解和對教學規律的把握。教師只有抓住了教學內容的規律線、知識之間的邏輯聯系線、數學思想方法的滲透線，才能設計出高質量的問題鏈。

（2）削枝才能強干——凝練問題，搭建問題鏈支架

問題宜精不宜多，要精心設計核心問題。所謂核心問題，是指能夠統整全課或某一教學環節、具有較大思考空間、能激發學生探究欲望的問題。把幾個核心問題按照一定的邏輯關系進行排序，就形成了問題鏈的“主鏈”。學生在解決核心問題的過程中逐步形成的下位的問題是問題鏈的“子鏈”，由此搭建問題鏈的支架。

筆者以“百分數的意義”一課為例，該課設計了如下的問題鏈支架：

圖2最上面第一層橫向呈現的問題是問題鏈的“主鏈”，由三個核心問題組成，是基于數學知識的本質以及概念教學的規律這一條暗線來進行設計的。概念教學一般會經歷“為什么產生——意義是什么——與已學的概念有什么聯系與區別”的過程。圖中每一個核心問題下面的問題是問題鏈的“子鏈”。當然，也不是所有的核心問題下面都需要形成一個子問題鏈，要視具體的情況而定。

（3）光合才能產出——多維互動，促問題鏈轉化

問題鏈基于教師的預設，成于師生的互動。無論是主問題鏈還是子問題鏈，都應是在師生、生生互動中生成的，不一定全部由學生提出，但是學生要見證它的生成。師生的多維互動就好像植物的光合作用，能產生“化學反應”，生成學生的數學學力，如問題解決能力、高階思維等。

（二）實現了兩大重要轉化

運用問題鏈導學，最終的落點應是學生的“學力生長”。筆者著力研究把“問題鏈”轉化為“思維活動鏈”和“學法鏈”的策略與方法。

1. 實現了“問題鏈→學法鏈”的轉化

本成果的問題鏈，更多指向的是基于課型特點、具有規律性和可遷移性的問題鏈模型，因此教學的“問題鏈”往往是該類問題的“學法鏈”，對問題鏈模型的領悟與掌握能有效提高學生的學習能力，從而在同類型知識的學習中遷移運用、舉一反三。

我們探索出把“問題鏈”轉化為“學法鏈”的有效實施策略（圖3）。

（1）問題可視化

在教學過程中把預設的問題或生成的問題通過PPT或板書顯性呈現，聽覺和視覺共同作用于學生，這樣既能體現問題鏈的建構過程，又讓學生明晰要探究的思路。

（2）問題生成性

教師應處理好精心預設與精彩生成的關系。從問題情境中引出要探究的問題，這些問題的提出盡可能來源于學生，這樣更有助于培養學生的思維，讓他們對學法有所感悟。

（3）問題鏈回顧與整體呈現

在某一個環節結束或全課總結時，引導學生回顧解決問題的過程，呈現之前一步步探究的問題，形成問題鏈，從而讓學生對學習過程有一個整體的認知，全面深刻感悟學法。

（4）同類溝通，學法提煉

把有代表性的幾節同類課的問題鏈放在同一頁PPT上，引導學生找出共性，從而歸納出具有一般意義的問題鏈，實現同類課學習方法的全線貫通。

2. 實現了“問題鏈→思維活動鏈”的轉化

設計形態的問題鏈并不等同于實施形態的思維活動鏈，這中間需要一定的轉化，轉化的途徑與方法主要有以下的幾個。

（1）精設情境，促問題生成

問題情境一般指現實情境和數學情境。能成功引發學生提出有價值問題的問題情境，不僅可以激發學生積極參與活動的“情”，更能引導學生浸潤于思維活動之“境”。比較有效的方法是，將知識生長點內隱于知識背景來創設問題情境。比如，百分數概念產生于比較的需要，與分數、倍、比、小數等數的概念存在層級關系，由此可以基于這樣的知識背景創設問題情境：“百分數”比“分數”多了一個“百”字，兩者有什么聯系與區別？我們已學習了分數，為什么還要學習百分數？在此基礎上借助“哪杯糖水更甜（已知每杯中糖和水的質量）”的情境，引導學生探究百分數的意義。

筆者還總結了“三不”的設計技巧，分別是“不完整”“不連貫”和“不一致”。簡單地說就是情境不是結構良好的，以此誘發學生發現問題和提出問題。另外提供給學生的情境，需要有問題的聚焦點，不能太發散，以此刺激學生的有效提問。

（2）善用追問，促思考深入

給學生思考和解決的問題，遵循先大后小的原則，先拋出或生成較大思考空間的問題（問題鏈框架中的核心問題），讓學生嘗試解決，當發現大部分學生有困難時，再進行引導。這個引導不是指教師的講解，而是追問。追問的主體可以是教師，也可以是學生，通過追問促進學生思考的深入。

（3）重視說理，促思維深刻

語言是思維的外殼，教師要重視學生的說理訓練，如讓學生說出解決問題的思考過程或推理的過程等，這個過程是學生運用邏輯思維組織數學語言，通過說、寫、畫等形式，數學地、有條理地表達思維的過程。引導學生進行交流與質疑也是說理和思維訓練的常用操作，學生在交流中吸納別人思維的閃光點，在質疑中理解、分析、評價，由此促進學生思維的深度參與，使他們的思維更加深刻和有條理。

（三）細化成六種課型變式

1. 解決問題教學的問題鏈支架

依據“解決問題教學的本質是數學建模”和解決問題教學的一般規律，筆者建構了如下的問題鏈基本模型（圖4）。

圖中橫向呈現的問題是問題鏈的“主鏈”，體現“現實原型→數學模型→運用模型”的模型建構和應用的過程。其中第一個核心問題的子問題鏈“閱讀與理解——分析與解答——回顧與反思”，是按照人教版教材解決問題的三個基本步驟設計的。

2. 計算教學的問題鏈支架

計算教學是“運算能力”培養的重要載體，運算能力主要包含三個方面的內涵：

運算能力正確運算，形成運算技能理解算理，知其所以然方法合理，運算途徑簡潔

因而計算教學的重點是理解算理和掌握算法，而理解算理又是教學的難點，根據計算教學的特點，其問題鏈的支架如圖5所示。

3. 統計教學的問題鏈支架

小學階段的統計教學，更多的是以統計圖表作為整理和描述數據的工具，然后進行數據分析的教學，其問題鏈的支架如圖6所示。

4. 概念教學的問題鏈支架

概念教學的主要環節為：概念的形成，概念的鞏固，概念的深化。依據概念教學的基本規律，其問題鏈支架設計如圖7所示。

5. 圖形與幾何教學的問題鏈支架

小學階段的圖形與幾何知識，主要包括四個方面，如圖8所示。

關于幾何圖形計算公式的推導，除基本圖形（長方形、長方體）是依據測量的本質屬性通過面積或體積單位的計數進行公式推導外，其余圖形的計算公式推導都是運用轉化的思想，基本的教學流程是：“猜想→驗證→推導→應用”，其問題鏈支架如圖9所示。

6. “數學廣角”和“綜合與實踐”教學的問題鏈支架

“數學廣角”和“綜合與實踐”的教學是培養學生“四基”和“四能”的重要載體，學生發現問題、提出問題、分析問題和解決問題這四個過程通常不是純線性的，在分析問題的過程中，會不斷地發現問題、分析問題和解決問題，也就是形成一個嵌套式問題鏈框架的形式，如圖10所示。

以上基于不同課型教學規律建構的問題鏈能有效助力學生在數學學習中的主動和意義建構，是學生學力生長的支架，也為教師進行問題設計提供了重要參考，起到了啟學引思、導學導教的作用。

3101500589203