架設知識生長結構立意考查核心素養

曹樹宏

【摘要】壓軸題的命題通常以知識生長結構為導向，逐步引導學生深入思考問題，打通條件與結論之間的道路，通過知識關系鏈的邏輯環環相扣，建立一條思維鏈，從而找到問題的解決方法.這樣命題設計起點低，立意高，又遵循學生思維從最近發展區走向未知發展區，不僅能考查學生的綜合能力，同時能檢驗和落實核心素養教學，是對深度學習效果的體現和延伸.

【關鍵詞】命題立意;知識生長結構;核心素養;指導教學

一、題目來源

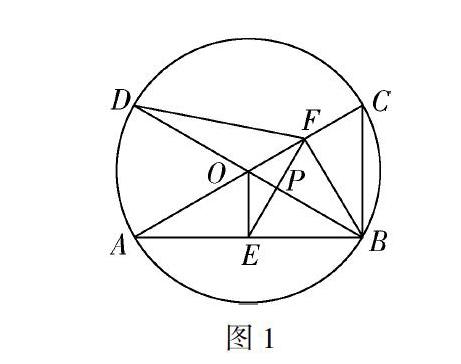
（2020杭州第23題）如圖1，已知AC，BD為⊙O的兩條直徑，連接AB，BC，OE⊥AB于點E，點F是半徑OC的中點，連接EF.

（1）設⊙O的半徑為1 ，若∠BAC=30°，求線段EF的長.

（2）連接BF，DF，設OB與EF交于點P.

① 求證：PE=PF.

② 若DF=EF，求∠BAC的度數.

本題文字不多，但信息量較大，條件比較豐富，有圓，有中點，有垂直，有特殊角，還側重考查幾何的圖形本質屬性;以教材基本圖形為知識生長點，架設知識生長結構.問題（1）主要就是特殊角條件下的解三角形問題，而且包括等腰三角形及直角三角形，比較容易找到思路.

本題中蘊含了豐富的基本圖形，不僅有中位線模型，還可以提煉出三角形比例線段基本圖形，正方形模型等.

二、問題內涵

（一）從特殊到一般

特殊性1：在問題（1）中，條件是“⊙O的半徑為1，∠BAC=30°”.實際上考查兩個基本知識點：（1）直徑所對的圓周角是90°;（2）含30°角的直角三角形性質.問題（1）的設計不僅能讓更多學生體會到成功的喜悅，還為學生繼續解決問題搭建了信心，是后續問題解決的知識生長點，以此為基礎架構知識生長結構.

問題（2）是以“OE⊥AB”聯想垂徑定理，以“點F是半徑OC的中點”聯想中點作用，為知識生長點逐漸展開自己的知識結構.

特殊性2：圓是數學中最常見的圖形之一，它既是軸對稱圖形也是中心對稱圖形，圓心和直徑是圓這一圖形的核心要素， 充分利用這一特性編制問題，能更好地考查學生對圖形本質的認識.以圖形的特性為生長點架構知識生長結構，尋找位置關系和數量關系是一條思維主線.

在問題（2）的解決中，利用對稱性就能啟發解決問題的思路.問題（2）是一個動態圖形，但題目條件“已知AC，BD為⊙O的兩條直徑，連接AB，BC，OE⊥AB于點E，點F是半徑OC的中點，連接EF.”決定了PE與PF的關系不變.學生要在動態圖形中發現并證明這一事實，必須能分析出“動態圖形中不變的量或關系”，容易聯想“中點”，從中點的作用入手找解決問題的方法.

（二）從靜態到動態

在分析一個幾何問題時，我們往往先著手觀察和分析圖形是“靜態”還是“動態”.對于“靜態圖形”問題處理起來比較容易，各位置的量是不變的，通常直接計算或證明，利用勾股定理或圖形基本性質就能完成;對于“動態圖形”需要分析點動、線動或形動，平移、旋轉、翻折等圖形變換.

問題（1）中，形狀大小是靜態的，即圓的大小不變，△ABC是含30°且斜邊為2的直角三角形不變，但是可以繞圓心旋轉，整體是動態的.不影響計算，因為三角形與圓的相對位置是靜態的.

問題（2）顯然是動態圖形，關注∠BAC的變化給圖形帶來的變化，問題顯然復雜起來，但是線段上中點位置是不變的，即點E相對于AB，點F相對于OC，點O相對于直徑AC與BD的位置都是不變的，這便是思考入手點，也是知識結構的生長點.

（三）從虛擬情境到實際情境

圓的情境往往是“虛擬”的，也就是說問題的本質落實在三角形問題上，只要把握這一認識，我們就可以在處理“圓”情境問題中做“減法”.比如可以將例題改編如下：

如圖2，已知線段AC，BD互相平分交于O點，且AC=BD.連接AB，BC，OE⊥AB于點E，點F是OC的中點，連接EF.

（1）設OC=1 ，若∠BAC=30°，求線段EF的長.

（2）連接BF，DF，設OB與EF交于點P.

① 求證：PE=PF.

② 若DF=EF，求∠BAC的度數.

這樣改編之后，思考進程絲毫不受影響，問題情境簡化，學生從“虛擬”圓情境回到真實的三角形問題情境中，反而有利于思考并找到解決方法.

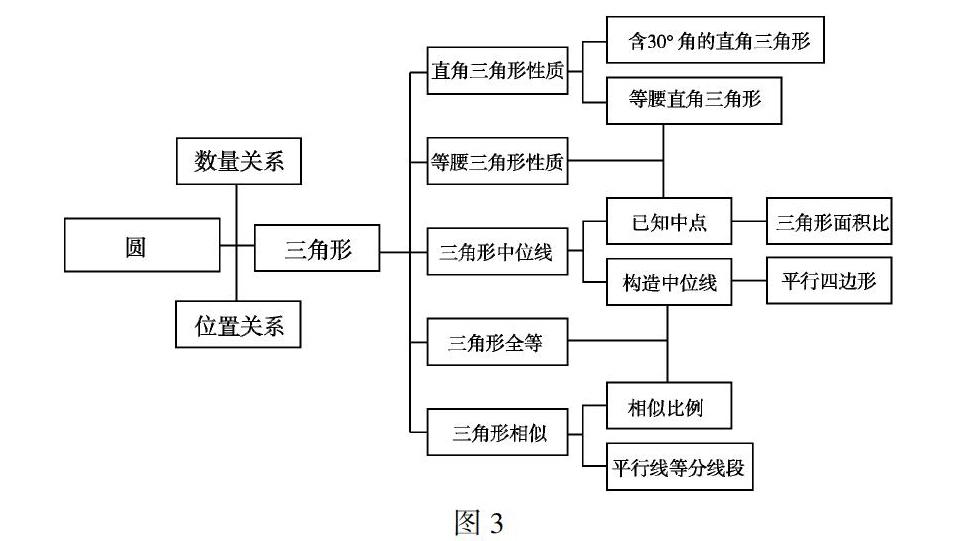
三、知識生長點

教師要深層次地尋覓思維活動軌跡，高標準地架設知識生長結構，才能教給學生具有生長力的數學，數學教學才能迸發出無與倫比的生命力量.

在解決問題（2）時，學生遇到很大的障礙，究其原因，是學生習慣把握方法，而忽視“知識生長點”尋源.問題（2）要證明相等的兩條線段在一條線上且共端點，顯然不能用熟悉的三角形知識去證明相等，學生的思路或方法容易受阻，這時就應該回憶平時見到這類問題的場景，搜索其他“結構”，探尋知識生長點，把握知識生長脈絡，找到平行四邊形或相似三角形來解決問題.

知識生長結構圖如下：

（一）生長點示例

生長點1：能否證明PE與PF兩條線段所在三角形△OEF或△BEF是等腰三角形？進而利用三線合一證明.（沒有條件）

生長點2：能否證明PE與PF兩條線段所在兩個三角形全等？（沒有發現）

生長點3：能否證明PE與PF兩條線段為兩個共斜邊直角三角形的斜中線？（沒有發現）

生長點4：PE與PF兩條線段能否通過第三條線段等量代換？（無法搭建第三條線段）

生長點5：能否證明PE與PF兩條線段所在兩個三角形等高且面積相等？（有想法，有待分析）

生長點6：能否證明PE與PF兩條線段為三角形相似的比例線段？（通過等量代換）

生長點7：能否證明PE與PF兩條線段是一個平行四邊形的對角線？（構造平行四邊形）

生長點8：PE與PF兩條線段能否通過平行線等分線段來證相等？（構造一組平行線）

生長點9：能否通過中位線證明？（構造模型圖形）

（二）幾種典型做法

方法1 利用生長點6

如圖4，過O作OG∥PE，交AB于G點，由OF∶OA=1∶2，得AG∶GE∶EB=2∶1∶3，再得OG∶FE=2∶3，PE∶OG=3∶4，得PE=PF.

問題（2）第②小題設計意圖更是強化核心素養的考查，學生需要做到以下幾點：（1）重新甄別圖形的變化;（2）構造正確圖形，提高畫圖能力;（3）由線相等帶來角度的變化（問題逆向設計）;（4）由“平行線等分線段”產生“位置關系轉化為數量關系”的知識結構.

分析：

由已知條件得到一個不變的關系量“FE=FB”是解決問題的關鍵.

如圖8，過點F作FG⊥AB交AB于G點，可得OE∥FG∥CB.

因為OF=CF，所以EG=BG，則FE=FB.

又因為FD=FE，所以FB=FD.

因為OD=OB，所以FO⊥BD.

所以△AOB是等腰直角三角形，所以∠BAC=45°.

其實，由此題條件“FD=FE”就把圖形從動態又轉化為靜態，此時兩條直徑互相垂直.這又可以回到基本模型上分析問題，充分把握FD=FB這一推想，問題迎刃而解.

在上述問題解答中，學生的思維不斷進行自我修正，以便找到自己曾經解決過得類似問題，沿著“知識生長線”這條路徑，思路慢慢打開，就能順利進行下一步.

四、問題立意 指導教學

（一）以概念為本 鋪設知識生長點

數學作為一種概念性語言，天然就適合開展概念為本的教學.平時我們只是在做數學，而沒有理解“做”的東西，這種傳統教學將數學當作一種程序和技能來教，并直接假定學生已經獲得概念性理解，而不是朝著概念性理解去教.概念為本的課堂教學中，更應將教學延伸至引導學生理解那些支持技能的概念性關系.

例如，在初三復習課中學習“中位線”時，要理解支持這個概念的是“全等三角形”“平行四邊形”“圖形旋轉變換”“相似三角形”等知識，這樣學生的思維建立起了知識網絡，在觀察圖形和分析圖形時，就有了視角，也有了發展和遷移的能力.

例如，如圖9，已知在△AEF中，E是AB的中點，O是AF上一點，且OF∶OA=1∶2，求證：PE=PF.

初三的學生對這個問題是比較熟悉的，但做好上述工作，學生有了前置概念的學習，容易產生以下解決問題的視角.

學生視角1：作平行線，構造中位線.

學生視角2：作平行線，構造全等三角形.

學生視角3：作平行線，用相似知識.

學生視角4：作平行線，利用面積關系.

（二）通過變式教學，架設知識生長結構

“單一的知識”發展到“復雜的問題”正是深度學習的要求， 我們有必要拓展對學習本質的認識，深入探尋學習和發展的內在機理，通過推動有意義的學習實踐來發展個體與復雜情境互動的綜合能力，從根本上把握并實現核心素養.

教學變式舉例

變式1：如圖10，在△ABC中，D是BC邊的中點，DE⊥BC交AB于點E，AD=AC，EC交AD于點F.

（1）求證：AF=FD;

（2）求證：FC=3EF.

變式2：如圖11，在正方形ABCD中，E為對角線AC上一點，連接BE，DE.F為BC上一點，且∠EFC+∠EDC=180°.

（1）求證：EB=EF;

（2）求證：AE∶EC=1∶3.

教師在教學中，要加強單元整體學習模式，形成一條知識鏈，這樣有利于學生思考問題的連續性和整體性，思維不容易斷.我們要認識到學習知識產生于發展過程，架設了知識結構，形成思維鏈，在結構的路線上或末端總能結出碩果.

【參考文獻】[1]卜以樓.“生長數學”：數學課堂教學的愿景[J].江蘇教育·中學教學版，2017（2）.

[2][3]林恩·埃里克森，洛伊斯·蘭寧.以概念為本的課程與教學：培養核心素養的絕佳實踐[M].魯效孔，譯. 上海：華東師范大學出版社，2018.

[4]肖思漢，雷浩.基于核心素養的課程建構[M].上海：華東師范大學出版社，2018.

[5]劉月霞，郭華.深度學習：走向核心素養（理論普及讀本）[M].北京：教育科學出版社，2018.