核心素養理念下的初中數學解題能力提升
陳建雙

【摘要】學生掌握了數學解題的有效途徑、技巧,則可以快速地解答數學問題,并有效運用數學知識,這與新課改下的學生學科核心素養培養目標相契合.因此,本文基于核心素養理念,對學生數學解題能力的培養展開相關研究,以期學生掌握有用的解題方法.
【關鍵詞】初中數學;解題;核心素養;方法
教師應從核心素養培養的角度,從學生的素養層面,引導學生掌握數學解題方法,從而讓學生掌握核心的數學解題思路,進而有效解答數學問題.下面本文將從代入、數形結合、化歸思維以及分類討論等解題角度,淺談引導學生學習與掌握有效的數學解題技巧與思路的方法.
一、從代入解題思維引導學生高效解答數學題目
首先,教師要指導學生正確分析數學題目,了解題目的來龍去脈,掌握數學題目中的重要信息點.然后,教師引導學生考慮數學題目是否可以運用代入解題思維,是否可以將題目進行代入簡化,促使學生了解數學代入解題思維的運用,幫助學生積累代入解題的經驗.
如題目:請看這個方程(a-4)x+b=a-bx-2,如果方程有無窮多個解,能否求解出a,b的值?
解題分析:在解答這道數學例題時,若學生不具備良好的代入解題思維,將會讓解題思路變得越來越復雜,從而影響到數學解題的效率,很難求解出問題的答案.對于此類數學方程問題,學生可以嘗試從代入求值角度理解和分析問題,從問題解答中逐漸養成良好的數學代入解題思維,真正理解數學問題,從而解答數學問題.比如,在上述方程中,可以得知方程是一個ax=b的形式,而教師可以引導學生從代入思維的角度,利用題目中的有效條件,也就是“方程有無窮多個解”這個解題條件,對數學題目中的問題展開代入解題分析,從而尋找數學問題中的知識點關系.
解題過程:根據已知條件及方程有無窮多個解,將方程(a-4)x+b=a-bx-2轉化為ax=b的形式,即(a+b-4)x=a-b-2.
由于方程有無窮多個解,可以獲知方程中未知數的系數和常數都為零,則可以運用代入解題思維,即令a+b-4=0,a-b-2=0,解得a=3,b=1.
可見,這道數學題目運用了代入法之后,整個解題效率得到了顯著提升,也讓學生發現數學解題內在的奧秘,從而有效提升學生的數學解題能力.
二、從數形結合思維引導學生有序解答數學題目
在數學解題過程中,數形結合解題思維也是一種重要、有效的數學解題思維,它有助于學生將復雜、抽象的數學題目轉化為生動形象的圖形問題.
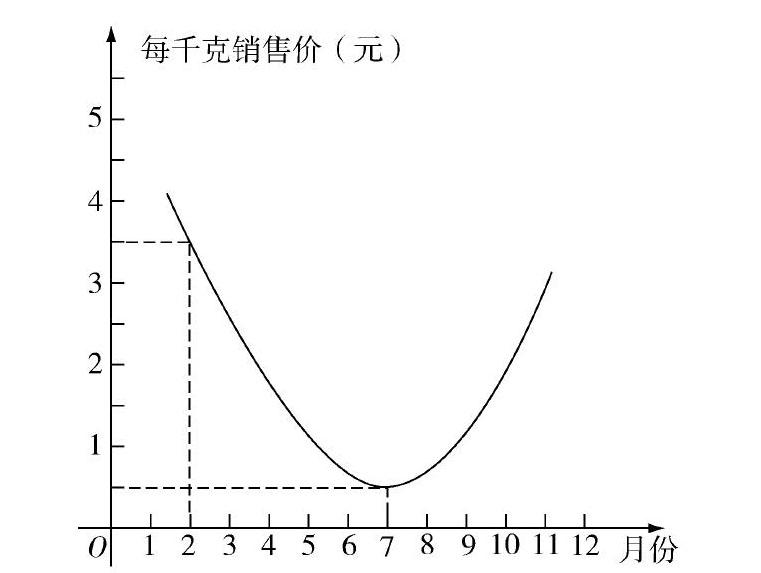
如題目:有一個農產品種植廠,其中銷售員小張根據往年的農產品銷售情況對今年的農產品銷售情況進行了預測,預測情況如圖所示,從圖中的拋物線可以看出農產品銷售價格與月份之間的關系,那么你還能從這張圖中獲得哪些農產品銷售情況?
解題分析:在這個數學問題中,學生可以運用二次函數的有關性質給出答案,如二次函數的增減性、對稱性、最大以及最小值等,而這些都需要學生深刻認知二次函數的圖像,學會利用數形結合思維實現數與形的有效轉換.比如,學生可以先分析題目中函數圖像的形狀,以此確定圖像屬于哪一種函數圖像,而根據題目中的函數圖形,可以判斷這是一個二次函數圖像.那么從函數圖像的開口方向、對稱軸的位置,可以看出函數圖像包含了諸多的知識信息,而這些都需要學生仔細去觀察,并且懂得結合圖形內容獲取數據信息,從而實現數與形的結合.
解題過程:根據題目中的問題,可以先從簡單的數軸分析開始,得出農產品銷售信息,如在圖像中,2月份農產品每千克銷售價格為3.5元;在1~7月這個時間段里,農產品價格在逐漸下降,主要依據就是這個時間段里函數y隨著x值的增大而逐漸變小;等等.
根據上述解答的過程,學生既可以懂得數形結合解題思維的價值,也能夠懂得靈活運用數量與圖形之間的關系可以順利解答問題.在運用數形結合思維的過程中,學生不僅可以提升自身的解題效率,也可以從中得到一定的解題經驗,這對學生日后的數學解題能力的提升有一定價值.
三、從化歸解題思維增強學生的數學解題能力
化歸解題思維是一種常見的數學解題思維,若學生掌握其中的要領,則有助于學生將復雜的數學問題簡單化.比如,在解答類似多元方程、高次方程等問題時,就可以運用數學轉化思維,將復雜、未知的數學方程問題進行適當變形,以轉化為簡單、直觀的整式方程,從而順利解題.
如題目:已知方程組
x+y=3,x-2y=a-3的解為正數,請求出a的取值范圍.
解題分析:觀察這個方程組,我們知道這是一個二元一次方程組,一般學生會直接解答,很少會運用一些解題技巧.雖然學生可以解出問題的答案,但是方法不夠靈活,因此,教師有必要跟學生講解一些解題技巧,如利用化歸思維將多元的方程組進行簡化,以盡可能提升解題效率.在這個問題中,學生可以運用化歸思維解答問題,先對方程進行適當變形,以將二元方程降為一元方程,從而使問題得到有效解決.
解題過程:根據已知方程組,先求出關于x,y的表達式,再根據題意進行不等式表示,從而組合成一個不等式組,進而將方程組問題轉化為不等式問題,最終把多元方程降為一元方程.其中,根據方程組的解為正數這個條件,可如下解題:
從這個問題的解答中,我們同樣看出數學解題技巧的重要性.學生只有掌握適當的數學解題技巧,才能快速解答問題,促使自身的解題能力得到有效提升.
四、以分類討論思維引導學生深入探究數學問題
在實際解題過程中,很多學生經常沒有按照數學題目所給的參數信息進行分類討論,而是直接對問題進行解答.學生必須學會對數學題目中的參數按層次進行分類討論,避免出現越級討論的現象,這樣才能運用最短的時間找到數學問題的答案.
解題分析:針對這一問題,學生可以利用分類討論思維,從不同角度分析問題可能存在的結果,以做到對數學問題的完整分析.學生可以對題目中參數a的取值范圍進行針對性討論,如對a=0和a≠0進行分類討論,從而得出問題的答案.
通過對數學問題進行分類討論,學生的解題思路更加清晰明朗,不會出現盲目解答的現象,而這需要學生既懂得尋找數學題目中的關鍵數據信息,也懂得對問題進行針對性的分類討論,從而做到對數學問題的全面分析,進而逐漸加深對數學知識的理解和運用,最終促使自己能夠順利解答問題.
五、結語
綜上所述,數學解題是學生理解和運用數學知識的重要途徑.在解答數學問題中,學生會遇到各種各樣的數學問題,而運用正確的解題思路進行數學問題的解答,是每一個學生需要思考和研究的問題.為了提升學生的數學解題能力,教師可以基于核心素養的角度,提升學生的解題能力,讓其懂得運用多元化的解題思維解答數學問題,這樣學生的數學解題能力才能得到真正提升.
【參考文獻】
[1] 肖繼春.基于核心素養下的初中數學解題教學研究[J].明日,2018,11(18):19.
[2] 鄭世春.核心素養理念下的初中數學課堂教學分析[J].讀寫算,2019,10(15):85.
[3] 張英,劉興存.核心素養理念下的初中數學課堂教學探究[J].課程教育研究,2019,13(23):26.

