應用GeoGebra軟件處理高中數學課堂教學難點

楊玉明

【摘要】幾何畫板是數學老師常用的教學輔助軟件，其規范和準備的繪圖功能，能把一些抽象的圖形運動過程直觀地展現在學生面前。隨著科技和信息化地日益發展，Markus Hohenwarter設計了一款新的動態教學軟件：GeoGebra。GeoGebra由Geometry和Algebra組合而成（以下簡稱GGB），同時擁有處理幾何繪圖與代數運算的能力，是進行數學教學、數學學習和數學研究的有力工具。

【關鍵詞】GeoGebra;高中數學;課堂教學

GGB軟件功能強大、繪圖工具齊全、使用簡單、交互性強，可以創作出許多數學藝術作品，特別是利用它可以揭示數學本質，體會數學魅力，從而提高學生的學習興趣。該軟件是數學學習的助手、數學教學的平臺、構建數學模型的工具。在高中數學的教學中很多老師碰到抽象的數學概念往往不知如何講解，講解了學生也無法理解。正所謂數缺形時少直觀，形少數時難入微，運用GGB軟件進行數學教學可以幫助我們解決這個難題。

一、GGB在三角函數教學中的應用

三角函數是高中數學重要的組成部分。初入高一的學生，對三角函數的學習常常感到不知所措，難于理解和掌握。如果使用傳統板書教學，不利于學生對三角函數的理解，這時使用GGB軟件將三角函數概念、公式、性質通過圖像精確表達，可以減輕教師的教學壓力，降低學生的思維難度，將抽象的數學公式圖形化也有利于學生理解和掌握新知識。

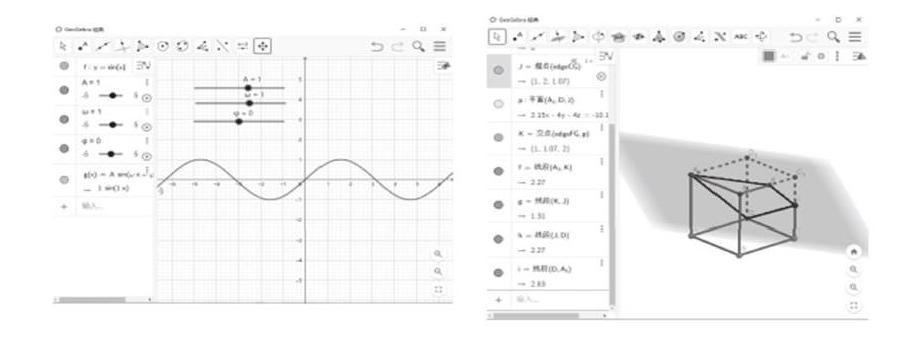
例如在講解三角函數y=Asin（ωx+ρ）的圖像時，運用GGB軟件教學可以讓學生直觀的觀察到A，ω，ρ變化時三角函數圖像是如何變化的。如圖，先畫出 y=sinx的圖像，再插入三條滑動條A，ω，ρ，再輸入函數y=Asin（ωx+ρ） 。

情形一、首先讓固定ω=1，ρ=0，讓A變動，讓學生觀察y=Asinx圖像隨A變化的變化情況，以及與y=sinx圖像的不同。接著固定A的值，令ω=1，讓ρ變動，讓學生觀察y=Asin（ωx+ρ）圖像隨ρ變化的變化情況，以及與y=sinx圖像的不同。最后固定A及ρ的值，讓ω變動，學生觀察y=Asin（ωx+ρ）圖像隨ω變化的變化情況，以及與y=sinx圖像的不同。

情形二、首先讓固定ω=1，ρ=0，讓A變動，讓學生觀察y=Asinx圖像隨A變化的變化情況，以及與y=sinx圖像的不同。

接著固定A的值，令ρ=0，讓ω變動，學生觀察y=Asinωx圖像隨ω變化的變化情況，以及與 y=sinx圖像的不同。最后固定A、ω的值，讓ρ變動，讓學生觀察y=Asin（ωx+ρ）圖像隨ρ變化的變化情況，以及與y=sinx圖像的不同。

二、GGB在立體幾何教學中的應用

立體幾何是高中數學重要的組成部分，也是高考重要的考點之一。但是大部分學生特別是女生在初學立體幾何時，空間想象能力欠缺，教師用傳統板書畫圖教授新知時，學生的思維還停留在平面幾何中。立體幾何具有較強的抽象性，空間概念和關系的建立，需要嚴密周到的思維和想象，如何幫助學生快速地從平面過渡到立體，從二維過渡到三維，我們可以利用GGB軟件中的3D繪圖功能構建三維立體圖形應用到實際教學中。

例如在立體幾何中碰到講解用一個動態的平面去截一個簡單幾何體的形成的截面形態問題時，教師要在黑板上畫出這個動態過程非常困難，學生要抽象出截面的形成過程也是十分困難，此時利用GGB軟件進行教學可以輕松地破解這一難題。在正方體ABCD-A1B1C1D1中，J是棱CC1上一點，平面過點A1，D，J，則平面截正方體的截面可以是什么圖形？如圖，在GGB的3D繪圖功能下，選擇正六面體工具畫出正方體ABCD-A1B1C1D1，在棱CC1上取一點J，利用過三點平面工具畫出過點A1，D，J的平面，利用交點工具畫出平面與正方體ABCD-A1B1C1D1各棱的交點，分別用線段工具連接A1，D，J與各棱的交點形成截面多邊形，然后點擊J點的動畫功能實現J點在棱CC1上動態運動，觀察J點運動時，截面的情況。

在立體幾何中，求幾何體的外接球半徑的題目，在學生心中是一類困難非常大的題目。教師在黑板上畫出空間位置關系進行講解時，學生在腦中抽象出所求幾何體的外接球是非常困難的，教師的教與學生的學不能順利的銜接。GGB的3D繪圖功能為我們進行這類題目的教學提供了強有力的工具。我們可以逐一構建長方體、正方體的外接球的3D模型、直三棱柱的外接球的3D模型、一側棱垂直于底面的棱錐的外接球的3D模型、正三棱錐的外接球的3D模型，讓學生直觀地觀察，體會此類題目圖形間的位置關系，數學本質。

三、GGB在解析幾何教學中的應用

在解析幾何的教學中，傳統的板書教學往往是使用純粹代數演算的方式來開展數學教學工作的。解析幾何的本質是幾何問題，圓錐曲線題目的設計脫離不了其平面幾何的背景。在進行解析幾何的教學中，教師要注重其幾何背景，合理運用數形結合往往能事半功倍。

GGB軟件繪圖工具齊全，同時具備很多軟件沒有的字母運算能力，交互性強，內置了圓錐曲線（同時會給出方程）、極線（反演）、切線（可以是圓、圓錐曲線或函數），在指令欄中直接輸入圓、圓錐曲線的方程即可繪制相應圖形。在進行圓錐曲線的定點、定形、定值問題的教學過程中，可以利用GGB軟件快速地繪制出圓錐曲線的圖形，根據題目的條件，利用GGB軟件的軌跡追蹤功能讓學生先觀察，再進行數學演算講解，能夠讓學生更容易地、更深刻地吸收知識。利用GGB軟件進行圓錐曲線教學研究，試題研究，可以舉一反三，可以從一道題擴展到一類題，可以驗證圓錐曲線試題設計的正確性，題目答案的正確性，這是傳統的教學方式所不能比擬的。

四、總結

GeoGebra作為一款融幾何、代數于一體的動態數學學科軟件，可以為我們構建所見即所得的情境。在技術的支持下，特別是在一些抽象問題的教學中，我們的教學可以更直觀的，這是傳統的教學模式是無法比擬的。

【參考文獻】

[1]GeoGebra官方網站 http：//www.GeoGebra.org.

[2]王貴軍.GeoGebra與數學實驗[M].北京：清華大學出版社，2020年10月