利用旋轉變換，提升初中生的數學思維

吉雪梅

摘? 要：數學學習的過程是學生不斷發現數學現象，并揭示其規律的過程。在教學過程中，教師要讓學生感知現象、探究現象，再跳出現象。總之，教師要讓學生的思維能力在對數學現象的探求中不斷得到提升與發展。

關鍵詞：初中數學;旋轉變換;數學思維

當前初中生的數學學習有很多停留在表層現象。教師要指導學生拓展思維，進入深度學習的狀態，即讓學生由某一點引申進行深入思考，進而將相關的問題串聯起來，形成一個完整的知識鏈。文章以人教版《義務教育教科書·數學》九年級上冊“旋轉”這一章節的知識點漫溯開去，運用圖形的旋轉構造全等的圖形進而整合分散的條件，以達到能夠巧妙解決問題的目的。

一、發現現象：提升學生的觀察能力

數學與生活緊密相連。在教學過程中，教師要讓學生發現一些數學現象，以讓他們思考這樣的現象在生活中還存在于哪些方面，這樣的現象有哪些性質等。這實際上是培養學生觀察能力的過程，教師要讓學生從多樣的生活中觀察到豐富的圖形，再從某些圖形中抽象出其中的一些關聯元素，發現哪些圖形在本質上是一樣的。發現問題，對學生學習數學非常重要。教師要將發現的機會交給學生，讓學生將自己的眼睛和大腦解放出來。

例如，在教學“旋轉”這一章節時，在傳統教學中，教師總是將旋轉的概念直接告訴學生，甚至在讓他們讀幾分鐘后，默寫這句話“把一個圖形繞著某一點旋轉一個角度的圖形變換叫作旋轉”。學生雖然記住了，但是未必能真正理解，更談不上再次探究。教師通過信息技術手段在白板上展示了多個三角形，讓學生去找一找他們認為有關聯的圖形。這個過程就像玩游戲一樣，學生立刻有了興趣，思維也活躍了。學生在尋找的同時，也在體會、理解旋轉的概念。當他們找出一個三角形在旋轉之后的另外一個圖形，他們就開始思考這兩個圖形之間有什么樣的關系，即旋轉具有什么性質。這需要學生將這兩個圖形畫下來觀察，在體驗中觀察。學生先是觀察到旋轉前后的圖形全等，然后教師追問學生有沒有其他發現。學生進而觀察到對應點與旋轉中心所連線段的夾角等于旋轉角。在這個過程中，學生的觀察能力得到鍛煉，數學思維能力自然也就提升了。

二、運用性質：提升學生的推理能力

知曉數學性質是學好數學的關鍵。知曉不是簡單地了解，而是要學以致用，將相關性質運用起來。學習數學性質的目的就是為了運用，在運用的過程中再深刻理解性質。學生的數學能力在很大程度上體現在他們運用知識的能力。運用是多元能力的綜合體現，而首要的就是推理能力，即運用性質推理可能存在的結果。

例如，在教學“旋轉”這一章節時，教師設置如下題目：點O是等邊三角形ABC內一點，已知∠AOB = 115°，∠BOC = 125°，則以線段OA，OB，OC為邊構成的三角形中，其內角度數分別是多少？列出題目條件后，學生發現這道題有點特殊，因為所給的條件比較分散。于是，學生就做出如下的推理設想：如果采用旋轉變換的方式，是不是可以集中處理？他們是這樣將設想轉變為現實的：先將△AOB繞點B順時針旋轉至△BDC;根據旋轉的性質，可以得出△BOD是等邊三角形，把OA，OB，OC轉化到△ODC中之后，學生進而推理出三角形中各個角的大小。明顯地，這個推理的過程是分為多步進行的，每一步的推理都是對旋轉性質的一次運用與深化。當然，旋轉性質的運用也不是單獨存在的，此題中也涉及全等三角形的性質、等邊三角形的性質和判定等。只不過，借助旋轉能讓推理變得更加簡潔，能讓解題變得更加巧妙。

三、拓展性質：提升學生的創新能力

在學習與運用旋轉這一性質之后，學生對這一數學現象有了更深刻的理解。但是，在學習之后，學生也會生成這樣的問題：老師在講課時列舉的例子是以三角形為主的，如果換成其他圖形（如正方形）會怎樣呢？旋轉變換得出的性質同樣是否適用于正方形？學生的提問就是他們創新能力涌現出來的一個表征。創新思維的生長說明學生不再僅僅滿足于教師的表述和舉證，開始有了自己的思考。

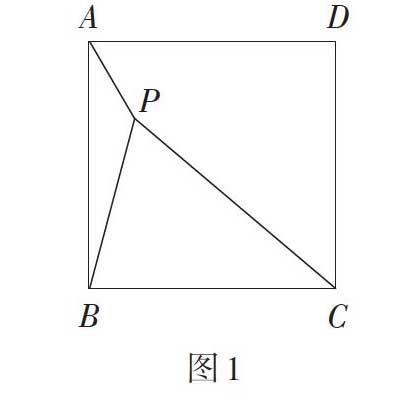
以下面這題為例，如圖1，P為正方形ABCD內一點，PA = 1，PB = 2，PC = 3，則∠APB的度數是多少？

同樣地，學生將剛才的旋轉三角形的相關經驗遷移到這道題目上來。他們認為此題條件相對分散，不容易直接運用。于是，學生借助旋轉，在解題中展開一系列的創新。如圖2，學生將△APB繞點B順時針旋轉90°，并連接PE，得到△BEC，進而得出△BEC ≌ △BPA，∠APB = ∠BEC。此題解題的關鍵在于將△APB繞點B順時針旋轉90°，并連接PE。

四、結束語

通過兩道題目的學習，學生能體會到旋轉變換在幾何解題中的作用。換而言之，學生通過圖形的旋轉達到集中條件、方便解題的目的。這個方便也體現在學生思維更容易迸發，能力更能集中生成。

參考文獻：

[1]顧彩梅. 挖掘旋轉本質? 再探最值隱蹤：初中數學深度學習的一次實踐與思考[J]. 上海中學數學，2019（12）.

[2]徐曉梅. 基于案例分析的初中數學幾何基本圖形教學探索[J]. 數學學習與研究，2019（12）.

[3]中華人民共和國教育部制定. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.