淺談初中數(shù)學(xué)習(xí)題課選題策略

林曉晶

摘 要：在初中數(shù)學(xué)教學(xué)中，習(xí)題課有著重要的作用。通過(guò)習(xí)題課的教學(xué)，能夠幫助學(xué)生掌握知識(shí)，提高學(xué)生的解題能力。因此在日常教學(xué)中，教師應(yīng)從學(xué)生的實(shí)際情況出發(fā)，對(duì)習(xí)題課的習(xí)題進(jìn)行合理的設(shè)計(jì)，提高教學(xué)質(zhì)量。本文結(jié)合本人的教學(xué)經(jīng)驗(yàn)，談一談習(xí)題課備課時(shí)的一些選題策略。

關(guān)鍵詞：初中數(shù)學(xué);習(xí)題課;勾股定理

隨著新課改的推行，初中數(shù)學(xué)習(xí)題教學(xué)方式逐漸發(fā)生變化，數(shù)學(xué)習(xí)題課不再是單純的題海戰(zhàn)術(shù)，而是通過(guò)有針對(duì)性、目的性的習(xí)題教學(xué)，解決當(dāng)前學(xué)生面對(duì)數(shù)學(xué)學(xué)習(xí)上的困難，實(shí)現(xiàn)對(duì)所學(xué)知識(shí)的靈活運(yùn)用。數(shù)學(xué)習(xí)題課作為初中數(shù)學(xué)教學(xué)中一種必不可少的課型，在教學(xué)中有著重要的作用。著名的數(shù)學(xué)教育家劉應(yīng)明曾經(jīng)提出過(guò)“通過(guò)數(shù)學(xué)教學(xué)來(lái)培養(yǎng)學(xué)生的能力，最基本而又可行的方法，就是加強(qiáng)數(shù)學(xué)習(xí)題課的作用”。[1]通過(guò)習(xí)題課的教學(xué)促使學(xué)生實(shí)際操作，促進(jìn)學(xué)生對(duì)知識(shí)的理解和掌握;通過(guò)習(xí)題課對(duì)知識(shí)點(diǎn)進(jìn)行專(zhuān)項(xiàng)歸納，提升學(xué)生解題技能和數(shù)學(xué)思維。因此，數(shù)學(xué)習(xí)題課的教學(xué)質(zhì)量影響著學(xué)生的數(shù)學(xué)成績(jī)。

然而在實(shí)際中數(shù)學(xué)習(xí)題課的教學(xué)中，有的教師不夠重視習(xí)題課，把習(xí)題課當(dāng)做一節(jié)作業(yè)講評(píng)課;有的教師習(xí)題課選題較為盲目，恨不得在一節(jié)課中把所有類(lèi)型的題目都選入，采用題海戰(zhàn)術(shù)，往往導(dǎo)致學(xué)生上完課后，抓不住本節(jié)課的重點(diǎn)內(nèi)容，對(duì)所學(xué)的知識(shí)似懂非懂，達(dá)不到習(xí)題課預(yù)期的教學(xué)目標(biāo)，無(wú)法提升習(xí)題課教學(xué)質(zhì)量。因此，要上好一節(jié)習(xí)題課，備課時(shí)習(xí)題的選擇就顯得非常重要，能夠讓學(xué)生掌握用本節(jié)課的知識(shí)和數(shù)學(xué)思想方法來(lái)解決相應(yīng)的數(shù)學(xué)問(wèn)題，是習(xí)題課教學(xué)所追求的目標(biāo)。本文以人教版八下勾股定理習(xí)題課中習(xí)題的選擇與設(shè)計(jì)為例，探討習(xí)題課備課選題時(shí)的幾點(diǎn)策略。

一、習(xí)題課選題的主要策略

（一）注重習(xí)題的典型性，針對(duì)性

教師要親自做大量題目，從中選題，挑選的習(xí)題要具有典型性，選擇從思維方式和解題方式上具有普遍指導(dǎo)性、代表性的題目作為例題，使學(xué)生能夠?qū)崿F(xiàn)會(huì)做一題，就掌握了解決這類(lèi)題目的數(shù)學(xué)思想和方法，從而會(huì)做一類(lèi)題目。同時(shí)，選題要符合本節(jié)課的教學(xué)目標(biāo)和教學(xué)重難點(diǎn)的要求，圍繞課本內(nèi)容，針對(duì)教材中的每一個(gè)知識(shí)點(diǎn)引申出不同類(lèi)型的題目;針對(duì)學(xué)生的現(xiàn)狀，薄弱點(diǎn)，易錯(cuò)點(diǎn)，挑選題目。習(xí)題的典型性和針對(duì)性不僅可以幫助學(xué)生鞏固和運(yùn)用基礎(chǔ)知識(shí)，還可以培養(yǎng)學(xué)生的數(shù)學(xué)思維，提高分析、解決數(shù)學(xué)問(wèn)題的能力。

（二）注重習(xí)題的層次性

班級(jí)學(xué)生的數(shù)學(xué)基礎(chǔ)和學(xué)習(xí)能力都存在一定的差異，針對(duì)學(xué)生層次的不同，挑選的習(xí)題既要有基礎(chǔ)性，也要有探究性，要有梯度。根據(jù)各個(gè)層次學(xué)生的特點(diǎn)選擇習(xí)題，因材施教，激起學(xué)生的求知欲，保護(hù)學(xué)生的學(xué)習(xí)自信心，并且滿(mǎn)足不同層次的學(xué)生對(duì)習(xí)題的不同要求，讓每個(gè)學(xué)生都能夠充分參與課堂，能夠有所收獲。同時(shí)，將習(xí)題由易到難，有層次的進(jìn)行安排，符合學(xué)生心理順序和學(xué)習(xí)規(guī)律，讓學(xué)生能夠接受本節(jié)課所學(xué)知識(shí)。

（三）注重習(xí)題的系統(tǒng)性

習(xí)題課中的習(xí)題需要有系統(tǒng)的呈現(xiàn)，需要圍繞一個(gè)主題或者知識(shí)點(diǎn)進(jìn)行選題，這樣知識(shí)才能夠被學(xué)生迅速、準(zhǔn)確、牢固的記憶，并能夠?qū)崿F(xiàn)對(duì)知識(shí)的靈活應(yīng)用。同時(shí)，教師應(yīng)該認(rèn)識(shí)到習(xí)題課不是單單由一堆習(xí)題堆積起來(lái)的，而是應(yīng)該要把習(xí)題按照一定的系統(tǒng)進(jìn)行安排，這樣才能幫助學(xué)生鞏固和深化基礎(chǔ)知識(shí)，梳理并完善知識(shí)結(jié)構(gòu)，形成系統(tǒng)地知識(shí)體系。

（四）注重習(xí)題的多樣性和靈活性

美國(guó)著名的數(shù)學(xué)教育家波利亞曾經(jīng)強(qiáng)調(diào)指出：掌握數(shù)學(xué)就意味著善于解題，不僅要善于解一些基礎(chǔ)題，而且要善于解一些要求獨(dú)立思考，思路合理，見(jiàn)解獨(dú)到和有發(fā)明創(chuàng)造的題。[2]習(xí)題的多樣性能夠激發(fā)學(xué)生獨(dú)立思考，從多角度、多方面開(kāi)發(fā)學(xué)生的思維，培養(yǎng)學(xué)生的能力，促進(jìn)學(xué)生多方面的能力發(fā)展。通過(guò)選擇具有一題多解，多題一解，開(kāi)放性答案，靈活性的習(xí)題，既開(kāi)闊了學(xué)生的思維，又使學(xué)生對(duì)本節(jié)課知識(shí)得認(rèn)知上升到更高層次的水平，從而培養(yǎng)了學(xué)生的綜合能力和核心素養(yǎng)。

二、教學(xué)案例

以下是本人在“人教版八下勾股定理習(xí)題課”教學(xué)中的選題和選題分析。

習(xí)題1：（1）在Rt△ABC中，∠C=90°，BC=12，AC=16，則AB的長(zhǎng)為_(kāi)_________

變式1：若一個(gè)直角三角形的三邊長(zhǎng)分別為3，4，x，則x的值__________

變式2：△ABC中，AB=15，AC=13，高AD=12，求BC的長(zhǎng).

設(shè)計(jì)意圖：習(xí)題1設(shè)計(jì)的主要目的是復(fù)習(xí)回顧勾股定理的基礎(chǔ)知識(shí)，懂得如何利用勾股定理進(jìn)行簡(jiǎn)單的應(yīng)用。本題中知二求一，知道直角三角形兩邊，求利用勾股定理直接求出直角三角形的的第三條邊長(zhǎng)。變式1和變式2則是在習(xí)題1的基礎(chǔ)上增加了難度，需要用到分類(lèi)討論的數(shù)學(xué)思想。

習(xí)題2：已知直角三角形的兩直角邊長(zhǎng)之比為3：4，斜邊長(zhǎng)為15，求兩直角邊的長(zhǎng);

變式3：已知直角三角形的周長(zhǎng)為30cm，斜邊長(zhǎng)為13cm，求此三角形的面積.

設(shè)計(jì)意圖：在直角三角形中知一邊且知另兩邊的數(shù)量關(guān)系，可以利用方程思想，列方程求出另外兩邊。習(xí)題2中直角邊的比已知，故可抓住此數(shù)量關(guān)系設(shè)元，用勾股定理列方程求解。變式3是習(xí)題2的提升，利用整體求解和方程的數(shù)學(xué)思想，皆可以解決。

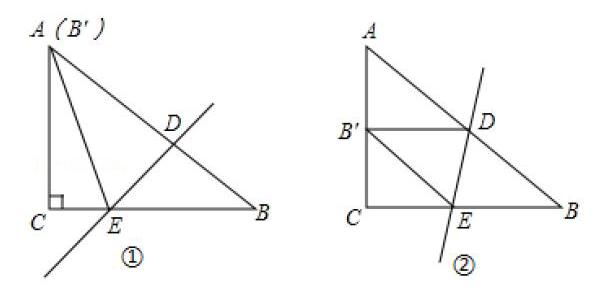
習(xí)題3：在Rt△ABC中，∠C=90°，AC=6，BC=8，點(diǎn)D、E分別是斜邊AB和直角邊BC上的點(diǎn)，把△ABC沿著直線(xiàn)DE折疊，頂點(diǎn)B的對(duì)應(yīng)點(diǎn)是點(diǎn)B′.

（1）如圖①，如果點(diǎn)B′和點(diǎn)A重合，求CE的長(zhǎng).

（2）如圖②，如果點(diǎn)B′落在直角邊AC的中點(diǎn)上，求BE的長(zhǎng).

變式4：有一塊直角三角形紙片，兩直角邊AC=6cm，BC=8cm.

（1）如圖1，現(xiàn)將紙片沿直線(xiàn)AD折疊，使直角邊AC落在斜邊AB上，則CD= ? ?cm.

（2）如圖2，若將直角∠C沿MN折疊，點(diǎn)C與AB中點(diǎn)H重合，點(diǎn)M、N分別在AC、BC上，則AM2、BN2與MN2之間有怎樣的數(shù)量關(guān)系？并證明你的結(jié)論.

設(shè)計(jì)意圖：在翻折問(wèn)題中，利用勾股定理結(jié)合折疊性質(zhì)去解決問(wèn)題，是折疊問(wèn)題中的典型方法。習(xí)題3體現(xiàn)了勾股定理在折疊問(wèn)題中的應(yīng)用，題中的兩個(gè)小題都是利用勾股定理和翻折性質(zhì)，找出圖形中所隱含的等量關(guān)系，利用方程思想可解決問(wèn)題。變式4則是對(duì)習(xí)題3的則進(jìn)行了思維拓展，此題的輔助線(xiàn)的作法是解題的關(guān)鍵，通過(guò)此題提升學(xué)生的數(shù)學(xué)思維和數(shù)學(xué)運(yùn)用能力。

三、案例分析

本節(jié)課是學(xué)習(xí)完勾股定理新授課后的習(xí)題課，學(xué)生對(duì)如何應(yīng)用勾股定理還不太熟悉，本節(jié)課的設(shè)計(jì)目的就是幫助學(xué)生熟練掌握和運(yùn)用勾股定理知識(shí)解決問(wèn)題。習(xí)題的選取除了圍繞勾股定理知識(shí)點(diǎn)進(jìn)行設(shè)計(jì)，還須要考慮學(xué)情，符合學(xué)生的心理特點(diǎn)，不能沒(méi)有難度梯度，以難題開(kāi)始，嚇到學(xué)生，應(yīng)該從基礎(chǔ)題目開(kāi)始，層層遞進(jìn)加深難度。例如，案例中的習(xí)題1作為本節(jié)課的切入題，該題是勾股定理應(yīng)用中的基礎(chǔ)題型，具有典型性，并且難度系數(shù)低，能夠讓所有學(xué)生參與其中。習(xí)題2難度稍有提升，讓學(xué)生在掌握上一題的基礎(chǔ)上，自然而然、順理成章地過(guò)渡到下一題的解題思路中去，具有層次性。使學(xué)生加深對(duì)勾股定理的理解，提高應(yīng)用能力。此外，本節(jié)課習(xí)題組中的部分題目具有一定的難度，需要綜合運(yùn)用所學(xué)的知識(shí)，如案例中的習(xí)題3，既注重對(duì)學(xué)生數(shù)學(xué)思維的訓(xùn)練，又注重對(duì)學(xué)生智力的開(kāi)發(fā)，更落腳于學(xué)生學(xué)科素養(yǎng)的培養(yǎng)。同時(shí)，每道習(xí)題后面都設(shè)計(jì)了相應(yīng)的變式練習(xí)，目的就是讓學(xué)生舉一反三，能夠從變式中尋找到解決此類(lèi)問(wèn)題的通法，使學(xué)生的思維更加靈活多變，提升學(xué)生的解題能力，從而提高習(xí)題課的課堂教學(xué)效率。本節(jié)習(xí)題課既能夠鞏固勾股定理的基礎(chǔ)知識(shí)，又能夠讓學(xué)生熟練掌握如何應(yīng)用勾股定理解決問(wèn)題，同時(shí)還彌補(bǔ)了新授課教學(xué)時(shí)沒(méi)傳達(dá)的數(shù)學(xué)思想方法，注重在教學(xué)中對(duì)學(xué)生的數(shù)學(xué)思想方法的滲透，對(duì)新授課的教學(xué)起到鞏固和補(bǔ)充作用。

四、結(jié)束語(yǔ)

當(dāng)然上好一節(jié)初中數(shù)學(xué)習(xí)題課除了如何備課選題之外，在平時(shí)的習(xí)題課教學(xué)時(shí)還有很多問(wèn)題值得深思和探討的。比如如何將學(xué)生講明白，如何引導(dǎo)學(xué)生思考，如何在課堂上激發(fā)學(xué)生的學(xué)習(xí)積極性……還需要更多的實(shí)踐經(jīng)驗(yàn)總結(jié)，本文只表達(dá)自己在習(xí)題課備課選題時(shí)一些粗淺的思考。總之，初中數(shù)學(xué)習(xí)題課是培養(yǎng)學(xué)生運(yùn)用數(shù)學(xué)知識(shí)分析問(wèn)題、解決問(wèn)題能力，并且實(shí)現(xiàn)知識(shí)飛躍的重要途徑。因此，我們需要不斷的完善習(xí)題課教學(xué)方法策略，習(xí)題課的習(xí)題選擇才會(huì)更加適合學(xué)生，適合課堂，從而達(dá)到我們用合適的習(xí)題來(lái)激發(fā)學(xué)生的求知欲，引發(fā)學(xué)生思考，提高課堂效率、提高學(xué)生的數(shù)學(xué)解題能力和數(shù)學(xué)素養(yǎng)目的。

參考文獻(xiàn)

[1]劉應(yīng)明等.我國(guó)數(shù)學(xué)高等教育面臨的挑戰(zhàn)和對(duì)策.面向21世紀(jì)的中國(guó)數(shù)學(xué)教育[z].南京：江蘇教育出版社，1994，（1）.

[2][美]R.E.莫里茲.數(shù)學(xué)家言行錄[M].南京江蘇教育出版社，1990.