例談綜合題的解法

史玨爾

【摘要】綜合題一般由一個較為復雜的圖形和幾個基本問題有機組合在一起的題目，它涉及到數學中較多的數學知識，并蘊涵著一定的數學思想方法。首先要會分解圖形，尋找到解綜合題的突破口，在此基礎上利用圖形的直觀性進行聯想、猜想、驗證與篩選，獲得解題方法的信息，然后利用綜合和分析的思維方法找到解題的方法，并結合各種數學思想方法和添加輔助線，使問題得到順利解決。

【關鍵詞】思維方法 ?數學思想方法 ? 直觀性 ?輔助線

綜合題是涉及數學中較多的數學知識的題目。一般的綜合題是由幾個基本問題有機地組合在一起，并蘊涵著一定的常見的數學思想方法。所以，在解綜合題時，只要分清題目的結構，把綜合性的問題，分解為若干個基本問題，同時注意運用數學思想方法，就能解答好。

一、分析圖形的結構。

1、綜合題往往有一個較為復雜的圖形。實際上，這種圖形往往是幾個常見的基本圖形有機地組合在一起。而學生要解答好綜合題，首先要會分解圖形，然后，從基本圖形著手，尋找到解綜合題的突破口。

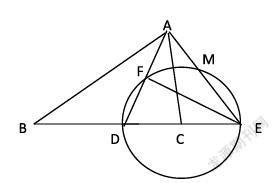
例1 ? 已知：在⊿ABC中，AD為∠BAC的角平分向，以C為圓心，CD為半徑的半圓交BC的延長線于點E，交AD與點F，交AE于點M，且∠B=∠CAE，FE：FD= 4：3。

求證：AF=DF;（2）求∠AED的余弦值;（3）如果BD=10，求⊿ABC的面

分析 ? 本題的圖形是曲直混合的圖形，所以顯得比價復雜。在此圖中，我們可以通過把EF⊥AD，和∠DAE=∠ADE的組合，分解出一個等腰三角形的三線合一的基本圖形。把∠B=∠CAE和∠AEB是公共角這兩個條件組合起來，又可以分解出⊿ABE∽⊿CAE。……