數(shù)學(xué)思考力：“探索與實踐”教學(xué)的應(yīng)然訴求

王蘇偉

[摘 要]小學(xué)數(shù)學(xué)蘇教版教材設(shè)置“探索與實踐”板塊的目的是讓教師充分利用觀察、實驗以及操作等相關(guān)活動，組織學(xué)生展開多元化的數(shù)學(xué)探究活動，揭示數(shù)學(xué)規(guī)律。在這一板塊的教學(xué)中，培養(yǎng)學(xué)生的數(shù)學(xué)思考力是重要的教學(xué)任務(wù)，通過引導(dǎo)動手操作，積累思考經(jīng)驗;組織數(shù)學(xué)探究，推進(jìn)思考進(jìn)程;強(qiáng)調(diào)數(shù)學(xué)反思，拓展思考空間的策略，能夠達(dá)到事半功倍的教學(xué)效果。

[關(guān)鍵詞]小學(xué)數(shù)學(xué);探索與實踐;數(shù)學(xué)思考力

[中圖分類號] G623.5[文獻(xiàn)標(biāo)識碼] A[文章編號] 1007-9068（2021）14-0076-02

蘇教版小學(xué)數(shù)學(xué)教材五、六年級的部分“整理與復(fù)習(xí)”中，特別編排了“探索與實踐”這一板塊內(nèi)容，這是對傳統(tǒng)教學(xué)模式的有效改革，更是一次嘗試，在內(nèi)容方面是全新的。“探索與實踐”關(guān)注的是學(xué)生對所學(xué)知識的應(yīng)用，同時也體現(xiàn)出典型的綜合性，能考驗學(xué)生的綜合數(shù)學(xué)思維，而這也是當(dāng)下數(shù)學(xué)教學(xué)中的薄弱環(huán)節(jié)。在這一板塊的教學(xué)中，培養(yǎng)學(xué)生的數(shù)學(xué)思考力是十分重要的。

一、引導(dǎo)動手操作，積累思考經(jīng)驗

基本活動經(jīng)驗需要學(xué)生借助操作活動而獲取，教師要善于運用操作活動，使學(xué)生能夠在這一過程中獲得數(shù)學(xué)體驗，積累豐富的感性體驗。

“探索與實踐”普遍是學(xué)習(xí)小組合作進(jìn)行的一種智力性游戲活動，具體的設(shè)計，首先需要呈現(xiàn)相應(yīng)的背景，明確價值指向，當(dāng)然還需要認(rèn)真解讀文本，這樣才能將問題的設(shè)計與教學(xué)內(nèi)容準(zhǔn)確結(jié)合在一起，更精準(zhǔn)地把握問題和教材內(nèi)容之間的關(guān)鍵連接點，使學(xué)生能夠從中體會到問題和數(shù)學(xué)知識之間的內(nèi)在聯(lián)系。

例如，在五年級下冊的“探索與實踐”中，有一道題是讓學(xué)生制作一個轉(zhuǎn)盤，在轉(zhuǎn)盤上分別標(biāo)注數(shù)字1、3、4、6、8、9，并與同桌完成以下任務(wù)：

（1）每人轉(zhuǎn)兩次轉(zhuǎn)盤，各自用得到的兩個數(shù)字組成一個真分?jǐn)?shù)（如果兩次轉(zhuǎn)到的數(shù)相同，可以再轉(zhuǎn)一次）;

（2）估算所組成的兩個分?jǐn)?shù)的大小，正確的一方得10分;

（3）多次反復(fù)進(jìn)行游戲，看誰先得到50分。

基于知識與能力這兩個視角展開分析，活動和數(shù)學(xué)知識之間的連接點非常多。就知識層面來看，包括真分?jǐn)?shù)的意義、分?jǐn)?shù)的化簡與大小比較等;就能力層面來看，包括學(xué)生思維敏捷性、表達(dá)的準(zhǔn)確性等。

活動指導(dǎo)：

（1）基礎(chǔ)準(zhǔn)備。首先復(fù)習(xí)和分?jǐn)?shù)相關(guān)的知識，例如分?jǐn)?shù)的含義、如何化簡、如何比較大小等。

（2）細(xì)化規(guī)則。題目給出的是活動要求，但沒有明確準(zhǔn)則，實際操作起來容易產(chǎn)生爭議，在經(jīng)過實踐和探討之后，教師制訂了具有可操作性的游戲規(guī)則：以同桌兩人為小組，其中一人先轉(zhuǎn)，得到真分?jǐn)?shù)，然后另一個人再轉(zhuǎn)，也得到真分?jǐn)?shù)。如果兩個真分?jǐn)?shù)不相等，則需要指明哪個大哪個小，如果相等，則需要說明原因;具體活動過程中，先判斷正確的人得10分，如果不能區(qū)分判斷正確的時間順序，則需要重賽;兩人都錯誤的情況下都不得分。

比賽結(jié)束后，教師請每個小組安排一名學(xué)生匯報具體的結(jié)果，目的是讓學(xué)生交流策略和心得，反思失敗的原因。通過操作活動，不僅學(xué)生成功地鞏固了知識，而且教師有效地實現(xiàn)了“激趣”這一目的，在培養(yǎng)學(xué)生的情感方面也取得顯著的效果，發(fā)展了學(xué)生的活動能力以及判斷能力。

二、組織數(shù)學(xué)探究，推進(jìn)思考進(jìn)程

數(shù)學(xué)和思維密不可分，特別是在小學(xué)數(shù)學(xué)教學(xué)實踐中，針對思維能力的培養(yǎng)是不可忽視的關(guān)鍵教學(xué)目標(biāo)，而“探索與實踐”最為突出的特點就是極強(qiáng)的活動性，因此，教師不僅要為學(xué)生創(chuàng)設(shè)多元的數(shù)學(xué)探究活動，還要使學(xué)生能夠在親歷活動的過程中提出問題和猜想，并結(jié)合自身的學(xué)力，完成觀察、思考、驗證等一系列思維活動，使學(xué)生在探究活動的過程中積累更為豐富的思維經(jīng)驗。

1.在探究中提升思維的深度

在數(shù)學(xué)學(xué)習(xí)過程中，學(xué)生針對學(xué)習(xí)對象常常會基于簡單的表層進(jìn)行感知，難以觸及本質(zhì)，這說明他們的思維缺乏深度。在“探索與實踐”這一板塊中，所涉及的內(nèi)容具有較強(qiáng)的綜合性，教師在教學(xué)時不僅要引導(dǎo)學(xué)生展開數(shù)學(xué)探究，還要提升學(xué)生的思維深度，這樣才有助于他們積累更豐富的數(shù)學(xué)思維經(jīng)驗。

例如，教師在“表面積為什么減少”這一道題的教學(xué)中，設(shè)計了兩個活動，使學(xué)生通過這兩個活動親歷數(shù)學(xué)知識的抽象過程。

首先，要求學(xué)生使用兩個邊長為1厘米的小正方體拼成一個長方體，學(xué)生在拼的過程中發(fā)現(xiàn)減少了兩個面的面積，教師趁機(jī)為學(xué)生呈現(xiàn)以下表格，要求學(xué)生自主填寫。

通過這一表格，學(xué)生總結(jié)出規(guī)律：在拼長方體的過程中，重疊的面越多，減少的表面積也就越多。

其次，教師提供10個同樣大小的小正方體，要求學(xué)生用它們拼成一個長方體，并提問：“有哪些不同的拼法？如果給所拼成的長方體包裝，哪種拼法用的包裝紙最少？”在進(jìn)行這個實踐操作活動時，學(xué)生首先需要猜想，然后結(jié)合具體的活動進(jìn)行驗證，從而從中總結(jié)出相應(yīng)的規(guī)律。

在上述教學(xué)案例中，兩個數(shù)學(xué)探究活動為學(xué)生提供了充足的時間和空間，使學(xué)生能在自主探究的過程中發(fā)現(xiàn)規(guī)律、總結(jié)規(guī)律。這樣的學(xué)習(xí)有助于學(xué)生豐富數(shù)學(xué)思維，獲得有效的經(jīng)驗。

2.在探究中拓展思維的廣度

思維的廣度重點在于開放性，在小學(xué)數(shù)學(xué)教學(xué)中，針對學(xué)生思維開放性的培養(yǎng)同樣非常關(guān)鍵，而“探索與實踐”這一板塊本身所涉及的內(nèi)容就具有開放性，教師可以利用這一內(nèi)容設(shè)計具有開放性的探究活動，使學(xué)生的思維得到有效拓展，豐富思維經(jīng)驗。

例如， a、b、c代表三個連續(xù)的自然數(shù)，任意寫下3組這樣的數(shù)，并求出各組的和。教學(xué)中，教師可以讓學(xué)生在表格中先寫出三個連續(xù)自然數(shù)，然后這樣對學(xué)生進(jìn)行引導(dǎo)：

（1）通過觀察表格，你有哪些發(fā)現(xiàn)？完成組內(nèi)交流;

（2）如果連續(xù)三個自然數(shù)的和為99，假如中間數(shù)為x，你是否能夠列出關(guān)于x的方程并求x的值？

（3）如果五個連續(xù)奇數(shù)的和為55，中間數(shù)為n，你能否列出關(guān)于n的方程并求n的值？

實際教學(xué)過程中，還需要設(shè)計巧妙的引導(dǎo)和追問，以此促進(jìn)學(xué)生思維的提升。

第一步：帶領(lǐng)學(xué)生探尋基本規(guī)律，也就是三個連續(xù)自然數(shù)的和等于中間數(shù)的3倍。

第二步：完成對基本規(guī)律的拓展，奇數(shù)個連續(xù)自然數(shù)的和也與中間數(shù)相關(guān)，是其與數(shù)字的個數(shù)之積。

第三步：針對基本規(guī)律的再次拓展，上一步所探討的是奇數(shù)個連續(xù)自然數(shù)之和，而奇數(shù)個連續(xù)偶數(shù)之和也可以選擇這一方法。

第四步：總結(jié)規(guī)律。

第五步：深入思考——偶數(shù)個連續(xù)自然數(shù)之和又存在怎樣的規(guī)律？

可見，教學(xué)過程中，要重視引導(dǎo)的作用。這些內(nèi)容既枯燥又抽象，如果能夠給予學(xué)生巧妙的引導(dǎo)，學(xué)生就能有較高的積極性，能主動大膽質(zhì)疑、踴躍發(fā)言，只有這樣才能使思維和探索一路同行。

三、強(qiáng)調(diào)數(shù)學(xué)反思，拓展思考空間

課程標(biāo)準(zhǔn)中特別強(qiáng)調(diào)學(xué)生對數(shù)學(xué)知識的應(yīng)用能力，以此促進(jìn)其數(shù)學(xué)積極情感的形成。“探索與實踐”中特別強(qiáng)調(diào)實踐的應(yīng)用性，因此實際教學(xué)過程中，不僅要組織多元的綜合數(shù)學(xué)活動，還要帶領(lǐng)學(xué)生完成活動過程的反思，積累豐富的數(shù)學(xué)應(yīng)用經(jīng)驗，這樣才能真正體現(xiàn)這一板塊的價值。課程標(biāo)準(zhǔn)中還特別強(qiáng)調(diào)針對應(yīng)用意識的培養(yǎng)，應(yīng)當(dāng)將其作為數(shù)學(xué)活動經(jīng)驗的核心，也是解決問題過程中不可或缺的關(guān)鍵要素，教師應(yīng)當(dāng)帶領(lǐng)學(xué)生反思具體的學(xué)習(xí)過程，特別是數(shù)學(xué)知識以及方法的應(yīng)用，這樣才有助于提高學(xué)生解決問題的能力。

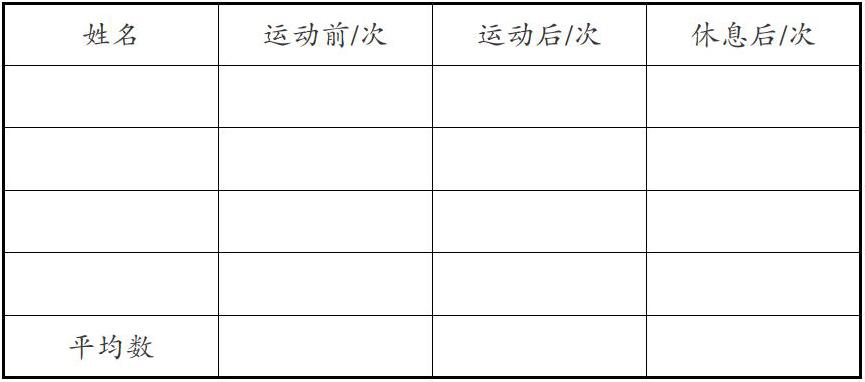
例如，在教學(xué)“運動與身體的變化”時，可為學(xué)生設(shè)計兩個數(shù)學(xué)探究活動。第一個是要求學(xué)生以4人為一組，分別測量運動之前每個人一分鐘內(nèi)的脈搏，然后原地高抬腿30次，再次測量一分鐘內(nèi)的脈搏，而后休息五分鐘又測量一次，并將所獲得的數(shù)據(jù)填入下面的表格中。

填寫完后，教師要求學(xué)生認(rèn)真觀察并計算平均數(shù)。在這過程中，學(xué)生發(fā)現(xiàn)，所有的成員的脈搏都呈現(xiàn)出顯著的變化：運動之前相對較慢，運動之后較快，休息以后轉(zhuǎn)慢。由此可以推測：人們在進(jìn)行運動之后，脈搏會加快。

第二個活動實際上是對上一活動所得出的結(jié)論而進(jìn)行的驗證，具體的驗證方法就是選擇另外一項體育運動，完成與上述相似的測試和記錄。通過這一活動可以順利驗證以上的結(jié)論，也能讓學(xué)生發(fā)現(xiàn)：當(dāng)人們所實施的運動強(qiáng)度不同時，脈搏的加快程度也會有所不同。

基于上述實踐活動，學(xué)生展開了自主測量、統(tǒng)計、計算以及歸納、梳理等一系列活動，不僅深刻體會到平均數(shù)在現(xiàn)實生活中的應(yīng)用，還感受到其價值，能夠立足于數(shù)學(xué)的視角，用數(shù)學(xué)知識解決問題，做到了學(xué)以致用。

總之，“探索與實踐”這一板塊對師生都具有極強(qiáng)的吸引力，因為其本身所具有的創(chuàng)新性能為數(shù)學(xué)課堂教學(xué)帶來蓬勃的生機(jī)和活力。在這一板塊的教學(xué)中，要把培養(yǎng)學(xué)生的數(shù)學(xué)思考力作為重要的教學(xué)任務(wù)，通過各種活動，達(dá)成事半功倍的教學(xué)效果。

【本文系江蘇省中小學(xué)教學(xué)研究課題《基于“探索與實踐”活動培養(yǎng)小學(xué)生數(shù)學(xué)思考力的實踐研究》研究成果，課題立項批準(zhǔn)號：2019JK13-L217。】

（責(zé)編 黃 露）