類比在高中數學教學中的應用手段探究

周菲菲

【摘要】高中數學的學科核心素養包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析.其中，邏輯推理包含歸納、類比、演繹.在高中數學教學中，教師應探究如何運用類比的思想方法使教學更加容易，讓數學知識“點線成面”，提高學生學習成效，鍛煉學生解決問題的能力.

【關鍵詞】類比;思想方法;核心素養;負遷移

類比，即“類比推理”，亦稱“類比法”，是根據兩個或兩類對象某些屬性的相同，推出它們的其他屬性也可能相同的推理方法.類比的過程是由此及彼的過程，從兩個對象具有某些相似或相同的屬性事實出發，推出其中一個對象可能具有另一個對象已具有的其他屬性.

天文學家開普勒說：“類比是我最可靠的老師.”哲學家康德說：“每當理智缺乏可靠論證的思路時，類比這個方法往往能指引我們前進.”作為一種思維方法，類比在人類生活、生產中得到了廣泛應用，發揮了巨大作用，深潛器、聽診器、活字印刷、飛機的減振裝置等的發明無不源于類比.

學科教學中，類比方法也被大量應用.教師在物理教學中，講電流的概念時，可用水流來類比;講電壓時，可用水壓來類比;類比電勢能和重力勢能的概念，電勢能和重力勢能的公式就不難理解了.教師在化學教學中講解電離平衡時，也可引導學生類比以前學過的化學平衡.

一、創設恰當的實例，類比生活情境

有些數學概念源于現實生活，是從生產、生活中抽象出來的.對于這些概念的教學，教師可以結合恰當的情境，類比一些感性的生活實例，引導學生提煉數學概念的本質屬性.

例1 高中數學集合概念教學

學生進入高中，接觸的第一個新知識就是集合，雖然在小學、初中及生活中對“同一類對象匯集在一起”有所感知，但對集合的無序性、互異性和確定性還是很難理解.

教師在教學中，可以類比生活實例，比如：教室中的35個學生組成一個“集合”，每個學生就是一個“元素”，每個學生“屬于”這個班級.每個學生都是不同的個體，這是元素的互異性;每個學生換座位之后，這個班級沒有改變，這是元素的無序性;某個學生是不是這個班級的一員，都會有一個明確的答案，這是元素的確定性.

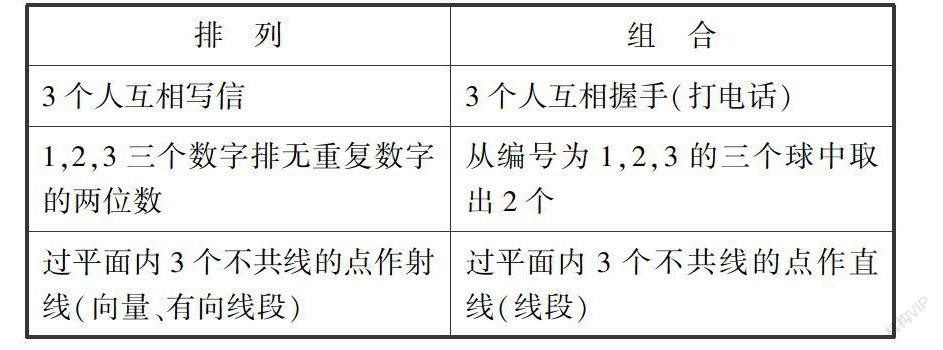
例2 排列組合概念的教學

理解排列組合的概念，分清有序、無序的區別是重難點.

教學中，教師可以將有序的兩兩排列類比為寫信，無序的兩兩組合類比為打電話、握手.

教師將學生耳熟能詳的生活實例引入概念教學的課堂，創設具體可感的生活情境，可以引導學生開展抽象的思維活動，在類比中獲得新知.

二、類比已學知識，遷移到新概念的學習

在數學教學過程中，我們常常會有“似曾相識”的感覺.我們可以把這些“類似”進行比較、聯想，將一個數學對象已知的特殊性質遷移到另一個數學對象上去，從而獲得另一個對象的性質.

（一）同章節知識點的類比

例3 指數函數和對數函數概念教學

教師可以做以下類比：

y=ax（a>1）y=ax（0

[]?? []

y=logax（a>1）y=logax（0

研究了指數函數在a>1時的解析式、定義域、值域、定點、單調性等性質之后，學生可以借助幾何畫板等信息化手段，畫出指數函數在a>1時的函數圖像，再結合列表的方式，可類比得出a>1時指數函數的相關性質.

研究了指數函數、學習了對數函數的概念后，在研究對數函數的性質時，也可以分為a>1和01時指數函數的性質，得出a>1時對數函數的性質，再類比得出0

從這個實例可以看出，類比是對知識進行理線穿點、融會貫通的好辦法.通過類比，學生既能從舊知中得出新知，還能成對、成串地鞏固兩組重要函數的性質.

在后續指數函數、對數函數的綜合練習中，經常會用到函數圖像輔助解題.解題時，往往可以通過y=2x的圖像類比得出y=3x，y=（12）x，y=13x，y=log2x，y=log3x，y=log12x，y=log13x的圖像，然后“看圖說話”，采用數形結合的方法即可輕松解決問題.

例4 等差數列、等比數列概念教學

通過下表類比，在類比的過程中，學生能感知到：在等差數列中相關的加法、減法、乘法運算，到等比數列中是對應的乘法、除法、乘方運算，這就像是運算的一種“升級”.

1.an=am+（n-m）d

2.等差數列中，等距離的項構成的數列仍然成等差數列

3.若m+n=t+s，則am+an=at+as

1.an=am·qn-m（q≠0）

2.等比數列中，等距離的項構成的數列仍然成等比數列

3.若m+n=t+s，則am·an=at·as

除此之外，同章節知識點的類比還可以運用在以下內容的學習中：

雙曲線與橢圓的概念、圖形、方程、性質、特征的類比;三角函數的幾組誘導公式的記憶、證明過程的類比;余弦函數與正弦函數的圖像、性質的類比;余弦定理與正弦定理的公式、適用范圍的類比;幾何概型與古典概型的概念、公式的類比;排列與組合的公式、模型的類比;線面平行與線面垂直的判定、性質定理的類比……

通過以上類比，學生不僅能識記、理解相關定義、公式、性質等，還可以感受到兩者之間的聯系，加深對概念的理解.

（二）不同學段知識點的類比

例5 對數概念教學

對數，對學生來說是一個陌生的名詞，教師在教學設計中，可以類比小學、初中所學知識，讓學生理解加減、乘除、乘方開方這些互逆運算，從而使對數的概念不那么突兀，讓學生明白，對數其實就是指數運算的一個逆運算.