以疑促思，構建高效數學課堂

尹江海

[摘? 要] 學貴有疑. 貫穿數學教學始終的疑問具有激發學生思考的重要作用. 想要構建高效數學課堂、培養學生的學科素養、提升學生的思維品質，自然離不開“疑”的有效促進. 文章以“軸對稱圖形”的教學為例，從課堂氛圍、情感體驗與持續思考三方面談以疑促思，構建高效數學課堂的具體方法.

[關鍵詞] 軸對稱圖形;以疑促思;高效課堂

新課程標準明確提出：“新課改的關鍵性舉措在于打破傳統機械性或接受型學習模式，提倡在學生主動參與中積極動手、動口、動腦，在疑問中探究，在合作中學習[1]”由此可見，構建高效課堂的主要抓手在于以疑促思，最大限度地發揮學生大腦的功能，引領學生在疑問的不斷產生、思考與解決中完成教學任務. 這是優化教學過程、整合三維目標、提高教學效率最好的方法，亦是促進學生全面發展的基本保障.

和諧的課堂氛圍是以疑促思，

構建高效課堂的前提

俗話說：“學起源于思，思源于疑. ”思與疑是相輔相成的關系，思能促使疑產生，疑能促進思發展. 和諧舒適的課堂氛圍是疑與思的溫床，學生在良好的氛圍中積極思考，并大膽想象、提出疑問. 課堂中，教師一個鼓勵的眼神、一個善意的微笑、一句贊美的言語或一個不經意的動作都能激起學生內心疑的漣漪，從而積極思考. 一個充滿歡笑、關愛、辯論與質疑的課堂，是學生不斷產生疑問、積極思考并解決疑問的陣地.

教學片段1

為了讓學生更直觀地體會軸對稱圖形的性質與特點，筆者在課堂上開展了“設計白紙圖案”的活動，以營造良好的課堂氛圍，鼓勵學生在動手操作中產生疑問并思考，以深化對知識的掌握.

師：請大家拿出事先準備好的紙張和剪刀. 現在我們進行今天的創意活動（學生都用期待的眼神看著老師）. 請大家將手中的紙張隨便怎么折，然后進行剪或者撕，看看能得出什么樣的圖案.

生1：老師你看，王某的圖案好丑.

師：哦？我來看看！還好啊，哪里丑了？

生2：他的圖案是用手撕的，左、右不一樣，不好看.

師：這個圖案只是不那么完美而已，為什么你覺得難看呢？

生2：因為這個圖的左、右兩邊不同.

生3：左、右兩邊不一樣就不是對稱圖形了.

師（對王某說）：生1嫌棄你的圖形不好看，是因為左、右不一樣，對嗎？（王某點頭認同）但是老師覺得挺好看的，因為生活中除了有對稱美，還有不對稱美. （王某微笑）現在我們一起來看看其他同學的作品.

大家把自己的圖案拿出來進行展示、對比.

生（齊）：好看的圖形都是左、右能夠重合的.

師：現在大家都認為對稱的圖形好看，那怎么描述對稱圖形呢？

生4：左、右兩邊一樣的圖形.

生5：對折后能完全重合的圖形.

生6：以一條直線為分界，位于直線兩側的圖形完全一樣.

……

同學們對剪出來或撕出來的圖形進行探討與交流，然后逐漸獲得軸對稱圖形的概念，思維在疑問的驅使下變得更為完整. 王某在教師善解人意的言語中也獲得了學習的動力. 課堂活動的設置一定要低門檻，要給每個層次的學生提供參與的機會. 學生在平等、友好的氛圍中，更容易促進元認知的發展■[2]. 在教師的鼓勵與賞識中獲得一種無形的精神力量，這比學到任何知識都重要.

真實可感的體驗是以疑促思，

構建高效課堂的基礎

對陌生事物產生好奇是人類的天性，也是疑問產生的主要來源之一. 教師根據學生的生活實際創設一些具有挑戰性而又真實可感的教學情境，能有效地誘發學生新的認知沖突，從而促進學生思維的發展，提高課堂效率.

教學片段2

為了吸引學生的注意力，筆者先播放一段關于圓的動畫，內容包括鐘表內部的齒輪轉動、騎行中自行車的車輪及轉動中的軸承等，讓學生感受圓的作用的同時，也讓學生對圓產生更加直觀、豐富的體驗. 在此基礎上展開相應的教學.

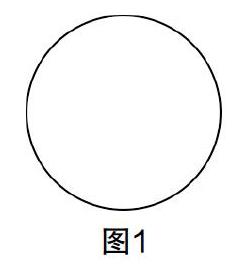
師：請大家開動腦筋想一想，如果我們想找到圖1這個圓的對稱軸，該怎么找.

生1：可以把這個圓的一半涂黑.

師：怎么知道多少是這個圓的一半？

生1：把這個圓折疊一下，就知道了.

生2：為什么要涂黑？直接折疊就行了.

生3：只要過圖1的圓心畫任意一條直線就行了.

師：很好！這個主意不錯. 但是我們不知道這個圓的圓心在哪兒呀，你們有沒有辦法找到這個圓心？

生4：如圖2，可以在這個圓上任取一條線段（弦）AB.

師：畫完線段以后該怎么辦呢？

生4：如圖3，再作線段AB的垂直平分線CD.

師：到了這一步還是不能確定圓心，該怎么辦呢？

生5：重復剛才的步驟，兩條垂直平分線的交點就是這個圓的圓心.

師：太棒了！還有沒有其他意見？

生6：我認為不需要重復剛才的步驟，只要作線段CD的垂直平分線，CD的垂直平分線和CD的交點就是圓心.

師：不錯. 找到圓心后，過圓心的任意一條直線都是這個圓的對稱軸.

此教學片段，教師巧妙地利用找圓心建立了圓的性質與軸對稱概念之間的聯系，學生親身經歷了尋找圓心的過程，這不但能讓學生對知識的發生發展過程產生更加直觀、深刻的印象，還對其思維的發展起到了良好的促進作用. 學生在積極的思考與親身體驗中獲得了解決問題的不同方案，整個過程體現了學生的思維在問題中得以生長.

持續思考的習慣是以疑促思，

構建高效課堂的關鍵

發現疑問與提出疑問應貫穿教學的全過程. 學生每解決完一個疑問，新的疑問將會接踵而至，而新的疑問又成了學生思考的起點. 因此，教師應使用各種手段，不斷地啟發學生產生疑問并思考，以促使有深度的問題鏈的產生，讓學生的思維在問題鏈中可持續發展. 所以，持續思考是實現以疑促思，構建高效課堂的關鍵.

教學片段3

在學生對軸對稱的概念有了一定了解的基礎上，教師可設計簡單的數學實驗，供學生產生有深度的問題鏈，從而讓學生保持持續思考的狀態，以促進思維的發展與課堂效率的提高.

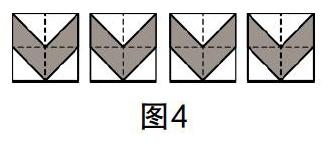
生活中的布匹、墻紙上的圖案都是由小圖案重復或拼接而來的，而小圖案又是由更小的圖案元素組合而成的. 現在我們將圖4中的圖案進行拼接，可得到各種圖案.

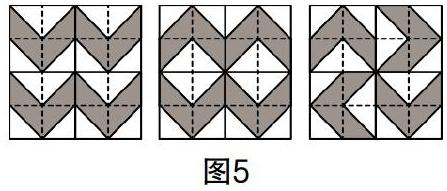
問題：（1）若拼接后的圖案為圖5所呈現的三種情況，請說一說其中具有旋轉對稱與軸對稱特征的圖案分別是哪個，并指出軸對稱圖案的對稱軸.

（2）請嘗試拼接出其他軸對稱圖案，并指出其對稱軸.

學生經思考與拼接后獲得了如圖6的圖案. 經討論與分析后發現，一些成對出現的圖案經旋轉或翻轉后還能出現重合的現象.

教師根據學生的最近發展區恰當地提出相應的問題，能在激發學生產生興趣的同時促使學生產生新的求知欲. 正如蘇霍姆林斯基所認為的那樣，每個人的內心深處都希望自己是一個發現者、探索者與研究者[3]. 筆者緊抓學生的這種心理需求，引導學生主動參與軸對稱知識的形成過程，將問題生活化的同時，由淺入深地引導學生逐漸形成問題鏈而持續地思考與分析，這樣不僅拓展了學生的求知思路，還讓學生的思維在釋疑中得以有效發展.

總之，數學教學是學生獲取知識、發現真理、答疑解惑的過程，作為教師，應盡可能地創造和諧的課堂氛圍，讓學生在真實可感的情感體驗中形成持續思考的習慣. 學生在視、聽、感、思等各個感覺器官的綜合作用下經歷設疑、質疑、釋疑的思考過程，在以疑促思中構建高效的數學課堂，這能為其學習能力的可持續發展奠定堅實的基礎.

參考文獻：

[1]中華人民共和國教育部. 義務教育數學課程標準（2011年版）[S]. 北京：北京師范大學出版社，2012.

[2]張慶林，邱江. 思維和學習領域中的元認知研究[J]. 西南大學學報：社會科學版， 2005，31（1）.

[3]裴昌根，宋乃慶，劉喬卉，牟少星. 數學學習興趣測評指標體系的構建與驗證[J]. 數學教育學報，2018（02）.