淺談如何有效進行初中數學“探索規律”教學

黃潔珊

摘要：初中數學知識繁雜瑣碎，但是經過研究可以發現，無論是數字和數字之間，還是圖形和圖形之間，甚至是數字和圖形之間，都存在著這樣或那樣的關聯，看似深奧的數學知識其實蘊含著奇妙的規律。本文就初中數學“探索規律”教學這一問題進行探究，并提出相關建議。

關鍵詞：初中數學;探索規律;有效教學

新課標提出“創新意識的培養是現代數學教育的基本任務，應體現在數學教與學的過程之中。學生自己發現和提出問題是創新的基礎;獨立思考、學會思考是創新的核心;歸納概括得到猜想和規律，并加以驗證，是創新的重要方法”。根據初中數學新課標提出的要求，教師應在教學過程中引導學生樹立積極主動探索數學奧秘的意識，增強他們的學習信心，幫助他們形成克服困難的意志力，從而提高學習數學的能力。

多年的教學發現，初中生在探索規律方面存在的問題主要有兩方面：一是非智力因素問題。部分學生對探索規律題掌握不全面，存在畏難心理，自信心不強，學習熱情不高，做題的時候畏手畏腳，無法準確分析題干的要求，正確解決問題。二是學習過程中出現的問題。基礎知識掌握不扎實、知識儲備不足;對數據的分析處理能力差，不能發現其中的本質;對具體情境中的關系不能準確的理解與表達;考慮問題不嚴謹，急于求得最后的結果，忽略一般性，缺乏驗證等。結合本人的教學實踐與經驗將從以下幾個方面淺談有效進行初中數學“探索規律”教學的幾點方法。

一、穩打穩扎，夯實基礎

教師在日常的教學過程中要重視學生基礎知識的掌握，對課本出現的概念、公式、定理要引導學生準確理解，并更多地讓學生進行限時訓練，讓學生在不斷分析問題、解決問題的過程中加深對本質的把握，把前后知識點聯系起來，提高知識的遷移能力。學生只有對基礎知識理解透徹，才能在解決實際問題中應用自如，準確地、全面地解決問題。

二、方法概括，按部就班

探索規律題的一般解題方法為：從特殊情形入手→探索發現規律→猜想結論→驗證結論→成立、得出結論，否則則回到第一步驟.讓學生準確地掌握探索規律的一般解題步驟，降低這類題型的神秘性，讓學生在解決問題時有據可依，有步驟可循。這一概括有利于幫助學生克服畏難心理，增強自信心，提高解題的能力。

三、回歸本質，融會貫通

在“探索規律”教學中，經常會出現學生對此類題型無從下手的現象，又或者把問題想得過于復雜。對此，教師可以在引入方面下功夫，由學生熟悉的、簡單的規律入手，充分調動學生的學習積極性。例如：在九年級的復習專題《探索規律》教學中，我是以學生熟悉的一些數列作為引入的。

觀察下列各數，并寫出第n（n≥1）個數的公式：

這幾個簡單例子的引入，快速地將學生的注意力集中到課堂，然后我根據例子引導學生自主探索出以上數列的規律，使學生初步感受規律題的本質，以達到舉一反三、融會貫通的目的，為接下來的探索規律教學做好鋪墊。

四、有效引導、化難為易

教師在課堂上有效、合理地引導學生積極主動地去探索規律，能夠促使學生極大地提高自己在數學學習方面的學習效果，從而有效地提升學生的綜合學習能力。

比如，在學習《數式運算規律》這一環節時，教師就可以組織學生仔細觀察相關數據，如“2”“6”“12”“20”“30”……，這組數據有著十分明顯的排列規律，每個數都可以用序列號來表示，“2”=1×2，“6”=2×3，“12”=3×4，“20”=4×5，“30”=5×6……學生能夠很輕松由此推出第10個數是多少，第n個數是多少。第十個數字顯然就是10×11=110，第n個數是n（n+1）。像這組數據的規律就是拆成有規律的兩個數進行相乘。但是，因為學生的程度有差異，個別學生由于做題經驗比較少，且可能不知道如何思考數據當中所蘊藏的規律，故而需要教師的積極引導。教師可讓學生嘗試歸納出對于一般的數式規律探索題的具體步驟：①標序列號;②對比序列號（1，2，3，…，n）和所給數字或數式的關系，把每一項與序列號之間的關系用含序列號的式子表示出來;③根據找出的規律求出第n個式子，并檢驗。

又如，在學習《圖形變化規律》這環節時，教師可以將單位圖形與復合圖形展示在學生面前，有具體形象的圖片在眼前，學生可以進行觀察與思考，擺脫思維的局限，靈活地解決問題。又比如：

下列圖形的排列是有一定的規律的，各組圖案里的三角形都是正三角形，第1個圖案有4個正三角形，第2個圖案有7個正三角形，第3個圖案有10個正三角形…按此規律擺下去，第n個圖案有 個正三角形（用含n的代數式表示）.

第1個圖案有4個正三角形，即4=3×1+1

第2個圖案有7個正三角形，即7=3×2+1

第3個圖案有10個正三角形，即10=3×3+1，…

按此規律擺下去，第n個圖案有（3n+1）個正三角形。

對于這類題型，教師只需要引導學生寫出前幾個圖形中的數量，分解出圖形中的數量關系，就可以輕松轉化為探究數式規律，這其實也反映了化歸的數學思想方法，幫助學生化難為易。

其實，我們在實踐中可以發現，圖形變化規律與算式運算規律雖然有著異曲同工之妙，但是對學生的理解卻造成了極大的挑戰。在課堂教學實踐中，教師需要通過簡單的圖形變化案例引導學生知道單位圖形的基本形狀，然后對復合圖形進行相應的分析，找出復合圖形當中單位圖形，這樣能夠促使學生對復合圖形產生一個科學而正確的認知，從而幫助學生找到正確的規律。

五、活用教材，有效延伸

數學教材是教師教學過程中必不可少的工具，在進行探究規律教學時，教師不能局限于只教“教材”，而應結合學生們在課堂上的表現以及對知識的掌握能力，創造性地使用教材，對其中的知識進行有效延伸，真正實現對教材的靈活運用。

例如，在學習《探索與表達規律》這一課時，教材中要求學生對日歷中3X3方框中個數字的規律進行探索，在整個教學內容完成之后，教師如果發現學生對這部分知識掌握得比較好，那么，教師可以適當將教材內容擴展到4X4的方框，進而帶領他們對16個數字的規律進行探究。對于學有余力的同學，教師還可以將教材中的知識擴展到對十字形的、豎列形、橫列形等數字規律的探究。利用延伸教材內容的方法，可以讓學生們的思維能力得到充分地開發，進一步激發他們探索數學知識的興趣，培養學生的發散性思維和創新能力，從而使他們的數學核心素養得到有效提升。

六、注重檢驗、養成習慣

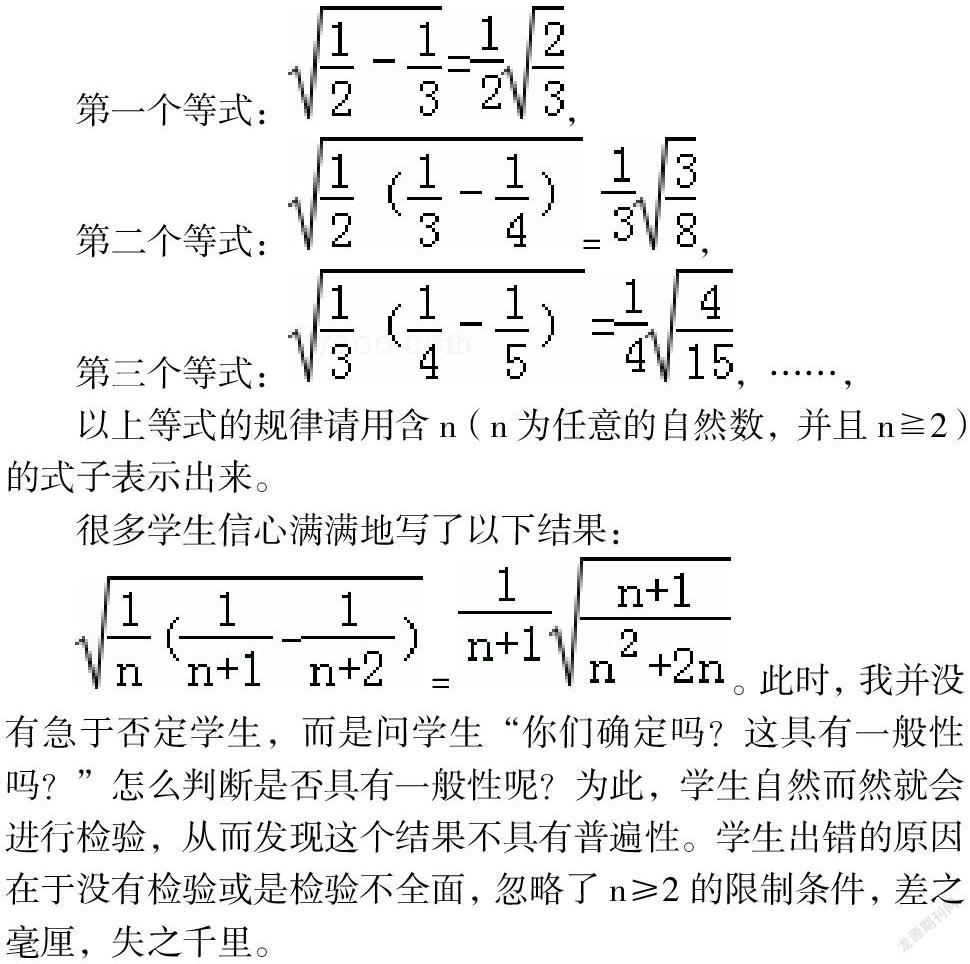
有些學生在做探索規律題時，沒有進行全面地分析，就急于寫下自以為對的結果，殊不知所寫的結果不具有一般性。之所以會出現這樣的錯誤就在于缺乏檢驗，探索規律必須遵循一定的步驟：特殊--猜想一般--驗證特殊。譬如，我在復習“探索規律”時給學生做過這一道題：觀察下列各個等式：

以上等式的規律請用含n（n為任意的自然數，并且n≧2）的式子表示出來。

很多學生信心滿滿地寫了以下結果：

=。此時，我并沒有急于否定學生，而是問學生“你們確定嗎？這具有一般性嗎？”怎么判斷是否具有一般性呢？為此，學生自然而然就會進行檢驗，從而發現這個結果不具有普遍性。學生出錯的原因在于沒有檢驗或是檢驗不全面，忽略了n≥2的限制條件，差之毫厘，失之千里。

通過這一例子，學生充分感受到“檢驗”這一步驟在做探索規律題時的重要性，這一過程既可以提高答題的準確率，又可以幫助學生克服學習惰性，形成良好的學習習慣，提高學習能力。

總而言之，學生是課堂的主體，教師在教學過程中作為學生的引導者，教師應不斷加強自身的學習，提高自身的教學水平。在教學中應采用有效的教學方法，設計必要的教學活動，結合學生的實際情況，讓學生通過觀察、發現、猜測、驗證進行探索性學習活動，循序漸進地培養學生的探索精神，掌握探索規律的相關解題技巧，從而使學生提高善于發現問題、大膽猜測問題和科學解決問題的能力，讓學生增強學習數學的興趣，發展學生的推理能力。

參考文獻：

[1]中華人民共和國教育部《義務教育數學課程標準》（2011年版），北京師范大學出版社

[2]邱有永.探索數學規律 培養學習能力[J].教育觀察，2019，8（02）：33-34.