淺談在小學數學教學中如何滲透數學思想

游衛萍

摘 要：小學數學課程對小學生的抽象思維能力、邏輯推理能力提出了較高的要求，因而，在小學數學教學中滲透數學思想能引導學生巧妙聯系數字與圖形，直觀理解所學內容，激發學習興趣，強化學習效果和提高教學質量。因此將數學思想滲透到小學數學教學中顯得尤為必要。

關鍵詞：小學數學教學;滲透;數學思想

從教三十余年，作為學校數學科組組長，筆者曾多次參與教研活動，也聽了不少課，發現很多教師在進行教學活動的時候往往只是重視數學知識和技能的傳授，關注的是這一節課的重點是否突出，難點是否已經突破，學生是否已經掌握了新的知識，而忽視了情感、態度、價值觀及數學思想滲透。《義務教育數學課程標準（2011年版）》明確提出“四基”課程目標，即基礎知識、基本技能、基本思想以及基本活動經驗。當前一些數學教師在進行教學的時候目標過于單一，如何才能改變這一現狀？筆者就這個問題提出以下幾個解決問題的策略和方法。

一、以教學用書為抓手，確定可滲透數學思想的內容

《教師教學用書》是教師開展教育教學活動的重要依據，因此一名合格的教師要讀懂教學用書，用好教學用書，在進行教學之前應該認真學習、研讀，明確教學目標、教學重點和教學難點，這樣我們的教學活動才不會偏離軌道。

首先要研讀教學用書的總述，明確這冊教材要滲透的數學思想有哪些。比如在一年級上冊的教學過程中經常會滲透的數學思想有：符號思想、模型思想、推理思想、函數思想、統計思想和集合思想等。再根據總述的指引找到對應的單元分析，仔細分析在本單元中有哪些課時會在教學中滲透數學思想。最后找到具體的課時，學習研究本節課要滲透的數學思想有哪些，如何在教學過程中滲透數學思想。

通過不斷深入學習和研究，教師要明確在這冊書中滲透數學思想的教學內容，做到心中有數。

二、以目標為導向，強化滲透數學思想的意識

明確需要滲透數學思想的教學內容之后，在教學目標設計中，既要有知識目標、技能目標，更要有情感、態度、價值觀、數學思想等多元化的目標，這樣的教學目標才是完整的。學生只有經歷完整的學習過程，才能學到知識，才能感受數學的魅力，才能培養邏輯思維能力，激發學習數學的興趣。

【案例1】平行四邊形的面積教學目標：

1. 讓學生通過動手操作，探索平行四邊形的面積公式。

2. 學會用平行四邊形的面積公式解決生活中的實際問題。

【案例2】平行四邊形的面積教學目標：

1. 讓學生通過動手操作，探索平行四邊形的面積公式。

2. 學會用平行四邊形的面積公式解決生活中的實際問題。

3. 通過觀察、分析平行四邊形面積公式的推導過程，讓學生學會運用轉化的思想方法解決數學問題，培養學生的邏輯思維能力。

對比上面兩個案例中的教學目標設置，能明顯看出案例1只重視知識技能目標，而忽略了情感、態度、價值觀及數學思想等其他目標。案例2的目標是多元化的，學生學到的知識是很全面的，不僅學會了平行四邊形的面積計算公式，還會用它來解決生活中的實際問題，學生還掌握了用轉化的思想方法解決問題的能力，發展學生的空間觀念，培養學生的邏輯思維能力，為將來的學習奠定良好的基礎。

三、以設計為依托，尋找教學中滲透數學思想的方法

教學設計包括知識板塊的設計和課時設計。在明確了應該滲透數學思想的知識后，在設計教學的時候就要考慮好如何在教學過程中滲透數學思想，如何將數學知識和數學思想有機地融合在一起。

【案例1】人教版五年級上冊第六單元——多邊形的面積

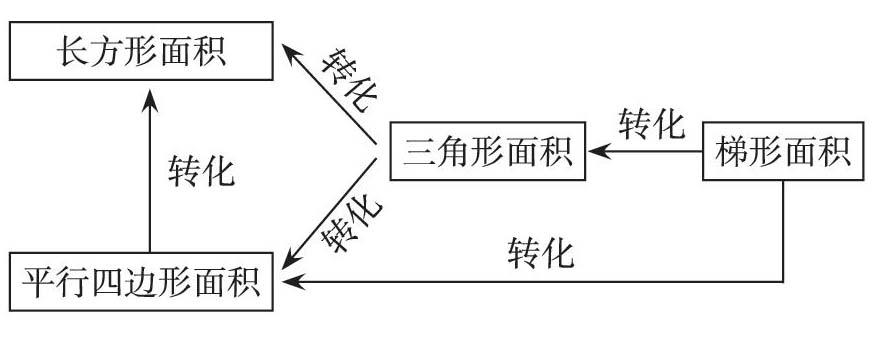
長方形面積計算是多邊形面積計算的基礎，通過剪、移、拼，我們可以將平行四邊形轉化成長方形，從而推導出平行四邊形的面積計算公式;用兩個完全相同的三角形拼成長方形、正方形或平行四邊形等學過的圖形，再推導出三角形的面積計算公式;同理，也可以用兩個完全相同的梯形拼成平行四邊形，推導出梯形的面積計算公式。學生在圖形轉化的過程中充分理解了圖形之間的內在聯系。在學習完這個知識板塊后要進行歸納、小結，實現知識的進一步提升，讓學生知道這個知識板塊基本上采用把未知知識轉化成已知知識的轉化思想進行學習，而且這種轉化的思想有利于以后的數學學習。

【案例2】人教版四年級上冊第五單元——平行與垂直

《平行與垂直》這節課，教學過程是這樣的：讓學生在白紙上畫兩條直線，收集學生的各種畫法，引導學生進行分類。通過探究，學生把它們分成兩類：相交和不相交。根據分類的結果，得出結論：在同一平面內不相交的兩條直線叫平行線。然后再將相交的幾種情況進行二次分類，分為相交成直角的和相交不成直角的，再次得出結論：兩條直線相交成直角，這兩條直線互相垂直。

很多數學教師的教學到了這里就止步了。最后一定要進行歸納總結：這節課我們用了分類思想進行學習，將同一平面內的兩條直線分成相交和不相交兩類，再把相交的分成垂直和不垂直兩類。教師的課后總結在此起到了畫龍點睛的作用，也能使學生進一步加深對知識的理解。

綜上所述，在數學教學過程中要上好一節課，首先要清楚地知道哪些教學內容是可以滲透數學思想的，在進行教學設計的時候要強化將數學知識和數學思想有機融合起來的意識，并在實施過程中將這些想法落到實處，這樣我們才會達到多元化的教學目標。

參考文獻：

[1]王光明，范文貴.新版課程標準解析與教學指導[M].北京：北京師范大學出版社，2012.

[2]史寧中.義務教育數學課程標準（2011年版）解讀[M].北京：北京師范大學出版社，2012.

[3]葉桂萍.數學思想方法在小學數學中的滲透[J].小學教學參考，2009（09）.