一題一課，提升學生的數學學科核心素養

王菲菲

摘要：初中數學復習課中往往充斥著大量的習題，如何將復習課上得更有效率、更有趣味，收到復習課該有的幫助學生深入理解知識點的效果，值得每位數學教師深入思考。與其凌亂的知識點堆疊，不如深挖一道題目，通過一題串連知識點，引導學生進行發散學習。文章以“全等三角形”的復習課為例，一題一課，進行變式教學，提升學生的數學學科核心素養。

關鍵詞：一題一課;全等三角形;變式教學;核心素養

在幾何學習中，存在一些基本圖形范式，教師要注重對基本圖形的形式進行變化，讓學生體會在變化的形式中不變的數學思想的，體驗數學的整體性。筆者針對“全等三角形”復習課中的一道例題研發了一節“一題一課”講評課，整理成文，以供研討。

一、教學過程與思考

環節1：經典例題呈現。

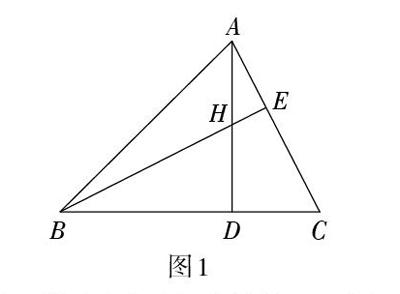
例1如圖1，AD=BD，AD⊥BC于點D，BE⊥AC于點E，AD與BE相交于點H。

（1）BH與AC相等嗎？為什么？（2）連接ED，求證ED平分∠BEC。

教學預設：第（1）小題比較簡單，大部分學生可以找到解題思路。在教學時，教師引導學生通過多種方式由AD⊥BC，BE⊥AC得到角相等的條件，由此證明△BHD≌△ACD。第（2）小題對于學生來說有一些難度，由于圖1中沒有涉及∠BED和∠CED的三角形全等，教師可以引導學生構造全等三角形來證明∠BED=∠CED。在此鋪墊下，讓學生小組交流討論，梳理思路，教師跟進點評。

【設計意圖】例1中的第（2）小題是服務于下文例2所增設的鋪墊題。例1整體屬于一道經典的中等難度題，作為這節課的開端，有利于幫助學生掌握相關知識。對于一些難度較大的習題，適當鋪墊更有利于拓展學生的思維，更符合學生的認知規律，能使學生的思維過程更具有階梯性和完整性。

環節2：形變質不變，感悟數學的變化美。

例2如圖2，AD=BD，AD⊥BC于點D，過點B作CA的垂線，交CA的延長線于點E，DA的延長線與BE的延長線相交于點H。

（1）BH與AC相等嗎？

（2）連接ED，求出∠DEH與∠ABD的數量關系。

教學預設：例1講評結束，教師引導學生感悟圖1

是如何生成的。首先是以含有45°角的直角三角板出發，畫出等腰直角三角形ABD;其次，在直角邊AD上任取一點H，連接BH并延長;最后，過點A作AE⊥BH于點E，交BD延長線于點C。那么，可以看出此時點H位于線段AD上，教師引領學生思考，若點H落在直線AD上，其他題干不變，例1中的第（1）小題的結論是否依然成立？此時學生可以輕松解決例2的第（1）小題，證明△BHD≌△ACD，得到BH=AC。

在例1第（2）小題的跟進講評后，學生對DE的特殊位置已經有了一些了解，可以類比證明例2中DE平分∠BEC，然后得出∠BED=45°。那么∠DEH的大小及其與∠ABD的數量關系問題就迎刃而解了。

【設計意圖】例2相較于例1而言，只改變了點H的位置，雖然改變了形式，但是題目結構與解題思路沒有變化。例1與例2相結合進行講解，有利于學生感悟數學的運動，讓學生深刻了解數學知識的精神內涵和其中包含的統一的數學思想方法，有效提高課堂教學效率。

二、教學立意的進一步闡釋

1.辨明結構，提升遷移能力

對于難度較大的幾何題，首先要辨析題目所反映的真正內容，探析題目的結構，化陌生為熟悉。學生對問題結構的理解受到具體題目情境的限制，就事論事，從整體結構去理解題目結構存在困難，這是比較普遍的現象。在等腰直角三角形這節課中有大量的經典題型和結論可以與平面直角坐標系相結合。在教學此類題目時，教師應該從平時的點滴滲透，引導學生遷移相似情境，提升學生的遷移能力。

2.變式教學，滲透思想方法

由例1到例2，變換題目背景，進行變式教學。變式教學是通過有目的地變換條件或情境，以凸顯數學概念或規律的本質屬性的教學。讓學生能在不同角度、不同層次、不同情形、不同背景下重新認識問題的本質。例2的題設對學生來說難度較大，而由例1引入，讓學生可以自然地聯想到例2可以轉化為例1的基本圖形，將復雜的題設簡單化，提煉出最關鍵的問題，進而解決問題，這種轉化與化歸的數學思想在數學學習過程中是非常重要的。

數學思想是數學學習的根，是學生能夠發現問題和解決問題的根本，沒有數學思想方法的教學，是沒有靈魂的，是浮于表面的。數學思想方法蘊涵于數學知識中。在平時教學中，教師潛移默化地滲透，才是幫助學生學習的有效方式，讓他們掌握思想方法，學會思考。

三、結束語

總之，在解題教學中，教師應該精心設計“再發現”的情境，讓學生能夠透過現象看本質，使學生的學習經歷認識形式變化的過程，在形式的運動變化過程中認識內容，體驗數學研究的過程及數學思想方法的復習教學真諦。文章僅以此題為例，設計了一節蘊涵形式變化與思想方法的課堂，期待更多專家同仁的批評指正。

參考文獻：

[1]章建躍，陶維林.注重學生思維參與和感悟的函數概念教學[J].數學通報，2009，48（6）.

[2]朱金祥，劉東升.數學教學中例題變式的策略：基于教學追問的視角[J].教育研究與評論（中學教育教學版），2016（9）.