用建模思想培養學生分析問題能力的幾點思考
張長利

摘要: 《義務教育數學課程標準》2011版中提出在數學課程中用數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力、模型思想、應用意識和創新意識十個核心詞闡釋了應當注意發展學生哪些基本的數學素養。曹培英老師撰寫的《跨越斷層,走出誤區》一書中說到:“數學模型”,目前尚無公認的定義,粗略來說,數學模型仍是針對或參照某種事物系統的特征和數學量關系,采取形式化的數學語言,概括地或近似地表達出來的一種數學結構,按廣義解釋,一切數學概念,數學理念體系,各種數學公式,各種方程以及由公式系列構成的算法系統等,都可以稱之為數學模型。狹義解釋,只有那些反映特定問題或特定的具體事物系統的數學關系結構,才叫做數學模型。這也是當今應用數學中數學模型的原意。“建模”是數學發展最初的原動力,模型思想的建立,是學生體會和理解數學與外部世界聯系的基本途徑,數學建模,是一種特殊的數學問題解決形式。
關鍵詞:建模思想;分析能力;思考
從教二十多年,聽了不少教師上解決問題的課堂教學,從教學過程的設計流程來看,大致可以歸納為:1.創設情景,提出問題,2.引導讀題,分析問題(主要是分析理解部分關鍵詞、句的意思),3.引導學生說出解答方法,列式解答,4.根據結果回顧反思,檢查計算結果是否正確,5.做相應的練習鞏固。
那么怎樣才能通過課堂的引領,讓學生真正建立起應用題的邏輯模型分析結構呢?學生在這種邏輯模型分析結構的幫助下,有入情入景的思維進程,就不會憑表面的感覺來錯誤地解決問題了。為此,我有幾下幾點思考:
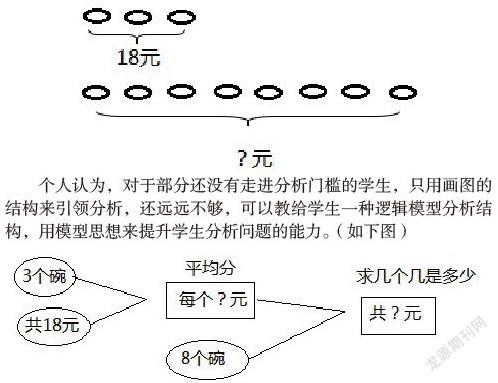
1.結合對應用題文字的理解,畫象形圖或線段圖,引領學生尋找有聯系的數量,求出相應的數學問題,畫出分析模型結構,逐步逼近最后問題的解決。如:小學數學三年級上冊六單元多位數乘一位數,學生學習了筆算方法后,都有相應數學問題解決板塊呈現,在71頁例8,媽媽買了3個碗,用了18元,如果買8個同樣的碗,需要多少錢?這是典型的歸總問題,但對于小學中低段的學生,這些莫生的概念,不能給他作過多的解釋,怎么才能不機械地把學生帶入到分析中來呢?有的老師采用了畫象形圖來幫助理解:(如圖)
個人認為,對于部分還沒有走進分析門檻的學生,只用畫圖的結構來引領分析,還遠遠不夠,可以教給學生一種邏輯模型分析結構,用模型思想來提升學生分析問題的能力。(如下圖)
由“3個碗”和“共18元”,能求出什么問題?怎樣計算?由“每個碗6元”和“8個碗”又能求什么問題?怎樣計算?有了這樣邏輯模型引領分析,學生仿佛帶上一盞燈,去尋找相關的兩個條件,逐步求出最后的問題,解答的方法也水到渠成。也可以反過來由最后的問題入手,去尋找解決問題需要的哪兩個條件,哪個條件沒有直接告知,又需要尋找哪兩個條件解答出來。這樣的邏輯模型結構,比教材中給我們呈現的由閱讀與理解→分析與解答 →回顧與反思這一模型結構更形象具體一些,并富有操作性。有了這樣的邏輯分析結構引領訓練,學生的邏輯分析能力才會真正得到鍛煉和提高。
2.在理解掌握了一些基本的數量關系后,可以結合具體的數量關系模型結構來進行分析,提高學生分析問題的能力。如:人教版五年級上冊學生在學習簡易方程中的解決問題例5:小林家和小云家相距4.5km。周日早上9:00兩人分別從家騎自行車相向而行,兩人何時相遇?這是學生在理解了速度、時間、路程數量關系后,進行的相遇問題的學習。教材在進入分析與解答步驟時,采用畫線段圖這種半抽象的模型結構引領學生進行分析,得出模型結構:小林騎的路程+小云騎的路程=總路程,個人認為只對于學優生來說,不會有什么困難,對于學困生來說,為什么要想小林騎的路程和小云騎的路程?是怎么思考的?它們的路程與總路程之間是什么關系?這些問題,如果沒有邏輯模型思考,學困生的思路一般不容易跟上,導致最后列出方程的模型解答不容易理解。可以在畫圖模型的分析上,結合前面學習理解的速度、時間、路程數量間的模型結構關系,幫助學困生小步走分析,提升他們的分析問題的能力。如下圖:
解:設兩人x分鐘后相遇。
3.根據具體的問題情景,可以用具體的動作演示加上文字的描述,建立情景模型,讓學生置身事件本身,提升理解能力。還是人教版五年級上冊學生在學習簡易方程中的解決問題例5:小林家和小云家相距4.5km。周日早上9:00兩人分別從家騎自行車相向而行,兩人何時相遇?在學生理解文字題意后,叫學生演示相遇問題情景模型結構,同時出發,騎1分鐘,按下暫停鍵,學生觀察小林騎了多遠?小云騎了多遠?兩人相距多遠?騎2分鐘,按下暫停,學生觀察小林行多遠?小林行多遠?隨著時間的變化,兩人相距的距離在逐步縮短,最后相遇時相距為0,把學生置于事件本身的情景模型中,才能真正理解相遇問題究竟是怎么回事,不會導致以后機械應用公式模型套用解答。
在實際教學中教師應盡可能留給學生更多的空間和時間去演繹問題的情景結構或數量關系結構,用模型結構去提高學生邏輯分析能力,讓孩子真正走進解決問題的分析過程,這樣才是真正有效的課堂,高效的課堂。
參考文獻:
[1]薛建忠.數學建模思想在小學數學教學中的應用研究[J].中華少年,2017(36):176-177.
[2]陳旭.淺談小學數學建模中的幾個問題[J].山東教育,2019(07):50.

