“圖形與幾何”課程內(nèi)容探析

劉久成

【摘 要】小學(xué)數(shù)學(xué)課程內(nèi)容“圖形與幾何”歷來是課程改革爭論的焦點之一。基于現(xiàn)實需要，以及數(shù)學(xué)學(xué)科和小學(xué)生認(rèn)知的特點，我們認(rèn)為，小學(xué)圖形與幾何課程內(nèi)容的確定應(yīng)關(guān)注以下幾個問題：學(xué)校教育的早期，教學(xué)歐氏幾何是重要的，但應(yīng)適當(dāng)拓展幾何課程內(nèi)容領(lǐng)域;幾何屬性的數(shù)量表示值得關(guān)注，并凸顯其直觀性;內(nèi)容呈現(xiàn)要重視情境設(shè)置和問題探索，體現(xiàn)從生活到數(shù)學(xué)、由直觀到抽象的特點，并保持?jǐn)?shù)學(xué)教材內(nèi)容一定的邏輯嚴(yán)謹(jǐn)性。

【關(guān)鍵詞】小學(xué)數(shù)學(xué) 圖形與幾何 課程內(nèi)容

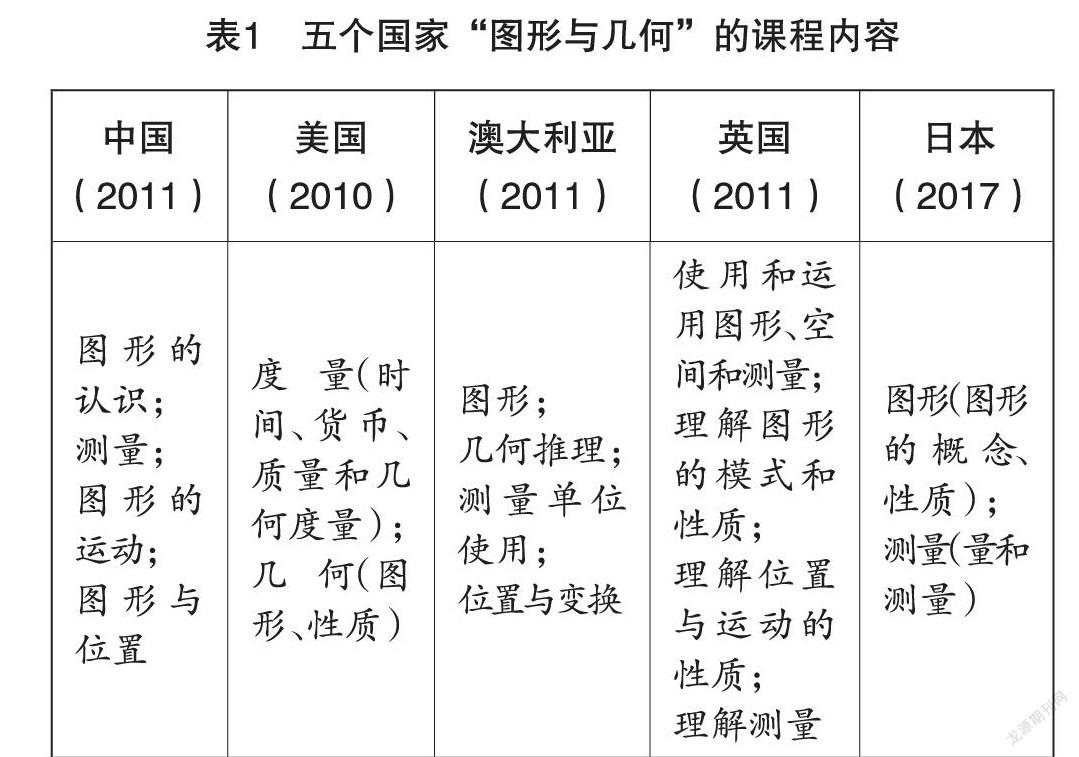
蘇聯(lián)學(xué)者斯托利亞爾曾說，不確定“教什么”的問題，就不可能解決“如何教”的問題。因此，“教什么”相對于“怎么教”來說是前提，如果教學(xué)內(nèi)容本身出了問題，那么再好的方法手段也無濟(jì)于事。幾何學(xué)是研究“形”的分支學(xué)科。幾何學(xué)的發(fā)展，讓人們看到了幾何的多樣性，也讓人們感受到，數(shù)學(xué)既有發(fā)現(xiàn)的特征，也有發(fā)明的特征。“圖形與幾何”是小學(xué)數(shù)學(xué)課程內(nèi)容之一，是幾何學(xué)最基礎(chǔ)的部分，其課程內(nèi)容改革一直是爭論的焦點之一。從表1中我們可以看到，中、美、澳、英、日五國現(xiàn)行課標(biāo)中關(guān)于圖形與幾何的課程內(nèi)容顯示出明顯的差異。

比較發(fā)現(xiàn)，各國圖形與幾何的教學(xué)內(nèi)容都有了拓廣，不再嚴(yán)守歐氏幾何概念體系，一般都涉及圖形的認(rèn)識、測量、變換與位置。通過具體比較可以發(fā)現(xiàn)，圖形與幾何內(nèi)容大多集中在對簡單二維和三維圖形特征的認(rèn)識上，但在內(nèi)容廣度和深度設(shè)置上有一定的區(qū)別。

20世紀(jì)70年代，斯托利亞爾在談到數(shù)學(xué)教育現(xiàn)代化時曾指出，幾何教學(xué)問題是數(shù)學(xué)教育現(xiàn)代化最復(fù)雜的問題之一，它引起了廣泛的、世界性的爭論。直到今天，圖形與幾何課程內(nèi)容仍然是數(shù)學(xué)課程中最不統(tǒng)一的一個部分。同時我們看到，新課改以來，對于圖形與幾何課程內(nèi)容的確定鮮有成果可以借鑒分析。由此，筆者基于現(xiàn)實需要，以及數(shù)學(xué)學(xué)科和小學(xué)生認(rèn)知的特點，提出小學(xué)圖形與幾何課程內(nèi)容的確定應(yīng)關(guān)注的幾個問題。

一、學(xué)校教育的早期，教學(xué)歐氏幾何是重要的，應(yīng)該鼓勵學(xué)生去研究簡單的幾何圖形，并探索這些圖形的性質(zhì)

歐氏幾何誕生兩千多年來，一直被視為學(xué)習(xí)幾何知識和培養(yǎng)學(xué)生邏輯思維的典范。20世紀(jì)60年代，曾有人建議中小學(xué)數(shù)學(xué)不再保留歐氏幾何體系。但時至今日，人們?nèi)匀徽J(rèn)為，歐氏幾何建立了一種最簡單、最直觀、最能為學(xué)生所接受的數(shù)學(xué)模型，是理解、描述和聯(lián)系現(xiàn)實空間的工具，讓學(xué)生利用這樣的模型去思考、去探索，可以使學(xué)生體驗到數(shù)學(xué)推理的力量。數(shù)學(xué)大師陳省身先生也指出：“一定要講歐氏幾何，從前歐幾里得幾何是整個教育的一部分，而不僅僅是數(shù)學(xué)的一部分。因為通過它可以使學(xué)生在簡單的情況下獲得一些推理。”歐氏幾何的直觀性、難度的層次性、真假的實驗性，以及推理過程的可預(yù)見性，使它成為訓(xùn)練邏輯思維和演繹推理的理想材料和工具。同時，我們看到，歐氏幾何的概念、性質(zhì)和相關(guān)測量在實際生活和生產(chǎn)實踐中有著極為廣泛的應(yīng)用，有助于學(xué)生感受數(shù)學(xué)的價值，激發(fā)學(xué)生對數(shù)學(xué)的興趣。當(dāng)然，在低年級，接近歐氏幾何的方式必須是非形式的和解釋性的，而系統(tǒng)化則留給較高年級。

二、小學(xué)圖形與幾何學(xué)習(xí)領(lǐng)域應(yīng)適當(dāng)拓展，更多地聯(lián)系生活實際，向?qū)W生展示圖形與幾何在生活實踐中的應(yīng)用，并讓學(xué)生感受到這些應(yīng)用會影響他們的生活

自20世紀(jì)貝利—克萊因運(yùn)動以來，人們開始重視實驗幾何、直觀幾何，將運(yùn)動思想引入幾何。我國進(jìn)行的本次課程改革也強(qiáng)調(diào)幾何變換，讓圖形“動起來”，在運(yùn)動和變換中研究和揭示圖形的性質(zhì)，雖未明確給出這些圖形變換的定義，但相關(guān)內(nèi)容已超出了歐氏幾何的概念體系。“圖形的運(yùn)動”在小學(xué)階段主要有兩種情況：一是形狀和大小不變，只是位置發(fā)生變化（合同運(yùn)動），包括軸對稱、平移、旋轉(zhuǎn);二是形狀不變，大小變化（相似運(yùn)動），如放大、縮小。本次課改之前，小學(xué)數(shù)學(xué)只涉及軸對稱圖形，不包含圖形的平移、旋轉(zhuǎn)和放大、縮小，現(xiàn)列入這些內(nèi)容至少有以下幾點理由：

一是解決實際問題的需要。弗賴登塔爾指出，數(shù)學(xué)的根源是常識，人們通過自己的實踐，把這些常識通過反思組織起來，不斷地進(jìn)行系統(tǒng)化。現(xiàn)實世界中，軸對稱、平移、旋轉(zhuǎn)的現(xiàn)象大量存在，觀察和認(rèn)識這些現(xiàn)象，有助于人們用數(shù)學(xué)的眼光觀察世界，用數(shù)學(xué)的思維思考世界，用數(shù)學(xué)的語言表達(dá)世界，提高認(rèn)識世界的能力。

二是歐氏幾何公理體系的建立，使它與邏輯推理結(jié)下了不解之緣，現(xiàn)在看來，邏輯推理也并非“歐氏幾何”所獨有。況且，除了發(fā)展學(xué)生的邏輯推理能力，還要發(fā)展其合情推理能力，以及觀察、操作、實驗、探究等方面的能力。因此在國際范圍內(nèi)，傳統(tǒng)意義上的歐氏幾何概念體系有逐漸被打破的趨勢，多樣化幾何進(jìn)入中小學(xué)課程已成為現(xiàn)實。圖形的運(yùn)動隸屬于變換幾何，寫進(jìn)義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)，使得幾何學(xué)習(xí)領(lǐng)域得到了拓展，也使小學(xué)幾何課程的內(nèi)容更為豐富。

三是“圖形的運(yùn)動”在于考查圖形在運(yùn)動下的不變性特征。這種數(shù)學(xué)思想方法非常重要。1872年，著名德國數(shù)學(xué)家、埃爾朗根大學(xué)教授菲利克斯·克萊茵提出的幾何學(xué)新定義，就是把幾何定義為一個變換群之下的不變性質(zhì)，并且引出了按照變換群對幾何進(jìn)行分類的思想。

四是軸對稱、平移、旋轉(zhuǎn)的內(nèi)容更具有現(xiàn)實性和操作性，其概念和性質(zhì)為圖案的設(shè)計、圖形面積的計算，以及認(rèn)識復(fù)雜圖形和全等圖形等奠定基礎(chǔ)。這些問題并非來自歐氏幾何，也無須要求學(xué)生了解相應(yīng)幾何領(lǐng)域的概念系統(tǒng)，但它對于提高學(xué)生研究圖形的興趣、提升學(xué)生的幾何直觀能力、發(fā)展學(xué)生的空間觀念和推理能力都很有幫助。

三、在小學(xué)，幾何屬性的數(shù)量表示是值得關(guān)注的領(lǐng)域

我們已經(jīng)看到，用代數(shù)的方法研究幾何具有重要的教育價值。17世紀(jì)法國數(shù)學(xué)家笛卡爾做了開創(chuàng)性工作，建立了解析幾何學(xué)。現(xiàn)行中學(xué)教材中引進(jìn)向量幾何的做法，也有助于幾何與代數(shù)的融合。因此，在小學(xué)適當(dāng)滲透坐標(biāo)思想，用數(shù)對或者方向與距離來表示位置，是空間位置的量化手段，不僅易于學(xué)生理解，也有利于中小學(xué)的銜接。同時坐標(biāo)幾何知識的運(yùn)用，也體現(xiàn)了數(shù)形結(jié)合的思想。

四、歷史地看，幾何課程內(nèi)容有如下幾個特征：直觀的、計算的、概念的、代數(shù)的、功利的、實用的，在制定小學(xué)數(shù)學(xué)課程內(nèi)容時必須做出選擇

我們看到，我國小學(xué)幾何在20世紀(jì)50年代強(qiáng)調(diào)計算（求積），70年代注重功利和實用，80年代至90年代直觀與計算并重，現(xiàn)行圖形與幾何課程內(nèi)容應(yīng)該更具綜合性，體現(xiàn)其直觀、計算和應(yīng)用的特點。內(nèi)容呈現(xiàn)重視情境設(shè)置和問題探索，體現(xiàn)從生活到數(shù)學(xué)、由直觀到抽象的特點。這就要求我們處理好不同情境類型的比重，特別是生活情境和數(shù)學(xué)學(xué)科情境的配合。過多的生活情境可能出現(xiàn)“去數(shù)學(xué)化”的傾向，數(shù)學(xué)自身的情境過多也會出現(xiàn)“去生活化”的傾向。小學(xué)生學(xué)習(xí)圖形與幾何，不是以公理體系為基礎(chǔ)而是以生活經(jīng)驗為基礎(chǔ)進(jìn)行的，兒童通過折疊、搭建、擺拼等操作活動，來積累表象，豐富經(jīng)驗，加深對圖形特征的理解。根據(jù)皮亞杰的研究，讓學(xué)生用尺規(guī)動手畫圖，可以促進(jìn)學(xué)生對幾何概念的理解，感悟圖形的存在。

比如，過兩點畫線段，可以讓學(xué)生感受線段的特征：直的、有兩個端點、可測量長度。

又如，過直線外一點，畫已知直線的平行線、垂線、垂線段，可以促進(jìn)學(xué)生感悟平行公理、垂線的唯一性、垂線段最短等性質(zhì)。

五、小學(xué)幾何課程內(nèi)容既要根植于兒童實際，又要言之有據(jù)，形成循序漸進(jìn)、互相連接的邏輯框架

學(xué)生學(xué)習(xí)圖形與幾何的基礎(chǔ)是生活經(jīng)驗，不可能跳過早期的直覺階段對幾何事實、概念進(jìn)行全面的理解。課程內(nèi)容的設(shè)計應(yīng)采取螺旋上升的方式，在不同水平上對同一課題進(jìn)行教學(xué)。現(xiàn)行教材一般是讓學(xué)生先直觀認(rèn)識簡單的幾何形體和常見的平面圖形，然后再進(jìn)行一維、二維、三維圖形的進(jìn)一步認(rèn)識。這樣循環(huán)交替、螺旋上升式的內(nèi)容設(shè)計，既考慮到數(shù)學(xué)知識的系統(tǒng)性，又兼顧了學(xué)生的認(rèn)知特點。

學(xué)習(xí)心理學(xué)研究表明：學(xué)生學(xué)習(xí)幾何，先有具體概念，再有定義概念。如認(rèn)識長方形和正方形，一年級先直觀認(rèn)識，此時學(xué)生只有具體概念，對圖像的識別建立在經(jīng)驗中的“形狀參照”。如像“門”一樣形狀的圖形就是長方形，像“地磚”一樣形狀的圖形就是正方形。學(xué)生在低年級對這些圖形僅僅是通過直觀的感知來積累表象，并且通過整體辨認(rèn)作出判斷，既不分析它們的特征，更談不上去研究它們的各個要素和邏輯聯(lián)系，到中年級時才逐步建立抽象概念，揭示它們的特征與關(guān)系。

再如，線段、射線、直線的教學(xué)內(nèi)容安排。1978年到新課改之前，都是在低年級先教學(xué)直線、線段，到中年級講“角”之前再引出射線，完成直線、線段、射線的教學(xué)。

這種做法，符合歐氏幾何概念體系，但容易出現(xiàn)一個問題：直線的無限延伸性往往被學(xué)生忽視，或者學(xué)生雖然記住了這一點，但對它缺乏深刻領(lǐng)悟和具體感受。事實上，“直線”概念有三個要素：直、無粗細(xì)可言和無限延伸性。其中，“直”和“無粗細(xì)可言”可以通過直觀教學(xué)并且運(yùn)用同一性抽象得出。如“直”可以通過教具演示、通過與“曲”的對比，使學(xué)生認(rèn)識。“無粗細(xì)可言”也可以借助典型事例的觀察和分析讓學(xué)生認(rèn)識到。如教室墻面的淺色區(qū)域和深色區(qū)域的分界線、折紙折出來的折痕等都是沒有粗細(xì)的線的例子。但“無限延伸性”難以通過直觀教學(xué)使學(xué)生獲得。因為我們找不到這樣的實際事例，“無限長的直觀教具”我們是拿不出來的。能拿出來的，只能是“有限的”。于是，這種無限延伸性只能由教師告訴學(xué)生，由學(xué)生發(fā)揮想象力。現(xiàn)行教材調(diào)整了教學(xué)順序，在低年級配合長度單位的教學(xué)先認(rèn)識線段，因為量長度本質(zhì)上是量線段的長度，從邏輯上說，應(yīng)該先有“線段”概念，到中年級講“角”的時候再引出射線、直線。這樣由具體到抽象，從有限到無限，既具有一定的邏輯性，又符合兒童的認(rèn)知特點。

注：本文系全國教育科學(xué)規(guī)劃教育部重點項目“改革開放以來小學(xué)數(shù)學(xué)教科書內(nèi)容嬗變及其經(jīng)驗研究”（編號：DHA190371）的研究成果。