初中數學“直觀想象”素養測評的實踐探索

摘要：直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養。以2020年江蘇省義務教育學業質量監測初中數學選擇題M8SO061為例，具體說明直觀想象素養測評試題的編改過程。可以發現，核心素養測評試題的難度控制手段主要有兩種：一是調整問題理解的難度，二是調整問題情境的復雜程度。

關鍵詞：直觀想象;學業質量監測;素養測評;初中數學

一、 直觀想象素養測評的實踐依據

（一） 直觀想象的內涵和表現

《普通高中數學課程標準（2017年版）》對“直觀想象”的描述為：“直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養。主要包括：借助空間形式認識事物的位置關系、形態變化與運動規律;利用圖形描述、分析數學問題;建立形與數的聯系，構建數學問題的直觀模型，探索解決問題的思路……直觀想象主要表現為：建立形與數的聯系，利用幾何圖形描述問題，借助幾何直觀理解問題，運用空間想象認識事物。”

（二） 直觀想象的評價要素

數學核心素養是個人在特定情境下形成的闡釋和應用數學的能力。數學核心素養的測評一般是通過設置相關的情境，并基于該情境要求學生運用數學學科的知識和技能、思想和方法完成某（幾）項任務，引發預期的行為表現，通過考察任務的完成質量來觀察、推斷學生的數學核心素養發展水平。

基于直觀想象的內涵和表現以及初中學生的認知水平，我們厘定了直觀想象素養的評價要素，包括：辨別對象所蘊含的數學要素，確定數學要素間的數學關系，形成表象，建立圖式;利用表象表示數學情境中的問題，利用表象表示現實情境中的數學問題，利用表象表示科學情境中的數學問題;借助圖式探索問題的解決思路，借助圖式完成問題的解決方案，借助圖式反思問題的解決過程。

二、 直觀想象素養測評的表現水平

（一） 借助空間認識事物的位置關系、形態變化與運動規律

1. 水平描述

水平A：能在實際情境中借助空間準確認識事物的位置關系、形態變化與運動規律。

水平B：能在復雜情境中借助空間認識事物的位置關系、形態變化與運動規律。

水平C：能在簡單情境中借助空間認識事物的位置關系、形態變化與運動規律。

水平D：不能借助空間認識簡單情境中事物的位置關系、形態變化與運動規律。

2. 相關示例

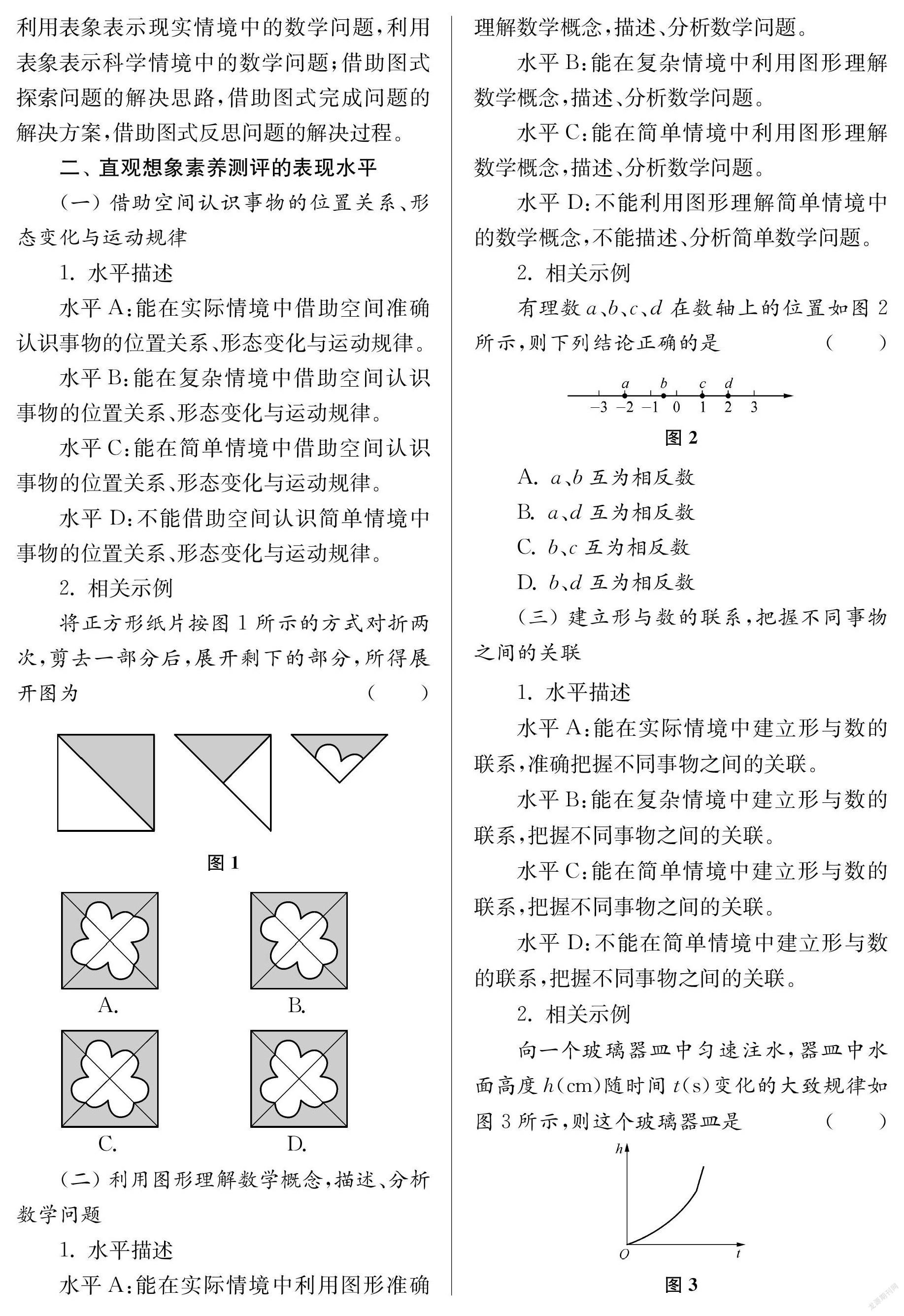
將正方形紙片按圖1所示的方式對折兩次，剪去一部分后，展開剩下的部分，所得展開圖為（）

A.B.

C.D.

（二） 利用圖形理解數學概念，描述、分析數學問題

1. 水平描述

水平A：能在實際情境中利用圖形準確理解數學概念，描述、分析數學問題。

水平B：能在復雜情境中利用圖形理解數學概念，描述、分析數學問題。

水平C：能在簡單情境中利用圖形理解數學概念，描述、分析數學問題。

水平D：不能利用圖形理解簡單情境中的數學概念，不能描述、分析簡單數學問題。

2. 相關示例

有理數a、b、c、d在數軸上的位置如圖2所示，則下列結論正確的是（）

A. a、b互為相反數

B. a、d互為相反數

C. b、c互為相反數

D. b、d互為相反數

（三） 建立形與數的聯系，把握不同事物之間的關聯

1. 水平描述

水平A：能在實際情境中建立形與數的聯系，準確把握不同事物之間的關聯。

水平B：能在復雜情境中建立形與數的聯系，把握不同事物之間的關聯。

水平C：能在簡單情境中建立形與數的聯系，把握不同事物之間的關聯。

水平D：不能在簡單情境中建立形與數的聯系，把握不同事物之間的關聯。

2. 相關示例

向一個玻璃器皿中勻速注水，器皿中水面高度h（cm）隨時間t（s）變化的大致規律如圖3所示，則這個玻璃器皿是（）

A.B.C.D.

三、 直觀想象素養測評的研究思路

對于直觀想象素養的測評，我們做了PISA測試數學試題、SAT數學試題、中學生數學建模競賽試題和日本初中生數學試題等系列材料的橫向對比研究，發現上述直觀想象素養的具體表現中，第一點和第二點的測評，學科情境比較多，生活情境有一些，科學情境鮮見;第三點的測評，學科情境、生活情境、科學情境均較為常見。我們認為，試題命制時應根據考查目標創設合適的試題情境，情境力求多樣化，學科情境、生活情境均有體現，通過情境激發外顯學生的直觀想象素養，從而真實評價學生直觀想象素養的水平層次。

表1所示即為2020年江蘇省義務教育學業質量監測中直觀想象素養測評試題命制的多維細目表。

四、 直觀想象素養測評的試題改進

2020年江蘇省義務教育學業質量監測中關于直觀想象素養的測評共4小題14分。本文以M8SO061為例，具體說明直觀想象素養測評試題的編改過程。

該題重點考查學生“建立形與數的聯系，把握不同事物之間的關聯”的直觀想象素養，需要學生結合圖像分析實際問題中的函數關系。

（一） 試題初稿及說明

小明晚飯后出門散步，圖4所示是小明離家的距離y與時間x之間的函數關系的圖像，若用五角星表示小明家的位置，則小明散步行走的路線可能是（）

復雜情境認識實際問題的函數圖像中特殊點的實際意義函數模型A.B.

C.D.

通過試測發現，該題學生得分率較低，除了正確答案C外，選擇答案A的學生較多。通過訪談了解到，學生的困惑主要在于函數圖像上的弧線在實際情境中的意義。項目組討論后認為，需要降低問題理解的難度，將函數圖像中的弧線改為水平的直線段。

（二） 試題過程稿及說明

小明晚飯后出門散步，圖5所示是小明離家的距離y與時間x之間的函數關系圖像，若用五角星表示小明家的位置，小明散步行走的路線可能是（）

A.B.

C.D.

通過二次試測發現，該題學生的得分率與預設的0.80仍有較大差距。通過訪談了解到，學生的困惑主要在于小明散步行走的路線有四種，每一種都要去想象它的函數圖像，太復雜了。項目組討論認為，需要降低問題情境的復雜程度，保留一種情境，讓學生根據情境選擇對應的函數圖像。

（三） 試題定稿及說明

小明晚飯后出門散步，行走的路線如圖6所示，則小明離家的距離h與散步時間t之間的函數關系可能是（）

A.B.

C.D.

從全省監測數據來看，該題學生的得分率為0.81，與預設難度基本吻合。由此可以發現，核心素養測評試題的難度控制手段主要有兩種：一是調整問題理解的難度，二是調整問題情境的復雜程度。我們可以根據試題的命制要求單獨使用或綜合使用。

參考文獻：

[1] 中華人民共和國教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018.

[2] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[3] 史寧中，林玉慈，陶劍，等.關于高中數學教育中的數學核心素養——史寧中教授訪談之七[J].課程·教材·教法，2017（4）.（石樹偉，江蘇省揚州市廣陵區教師發展中心，特級教師，正高級教師。江蘇省教育學會中學數學教學專業委員會理事。“國培計劃”優秀工作坊主持人，江蘇省優秀教育工作者，江蘇省教科研系統先進個人。）