淺談初中數學函數教學的有效方法

鄒崇春

摘 要：初中函數是初中數學學科教學中的重要內容，函數知識比較枯燥抽象，學生學習有一定的難度。在教學中要與生活實際緊密聯系，注重類比教學方法的應用。初步培養學生的建模思想，在教學中合理使用多媒體輔助教學，幫助學生對函數的概念、圖像、性質的深刻理解運用。不斷探索有效的教學方法，提高課堂教學效率。

關鍵詞：初中數學;函數教學;方法

引言

初中階段學習的一次函數、反比例函數、二次函數，是初中數學課程中的主要知識點，也是學生掌握的較難知識點。這部分知識概念、圖像、性質等均具抽象性。教師們認為函數難講，學生也認為這部分題很難做。因此進行初中數學函數知識教學方法的研究，可有效提高函數知識的教學水平。作為一名初中數學老師，在數學課程教學中，應重視函數教學策略研討，不斷創新函數教學方法。下面談點個人淺顯認識：

一.要培養學生對函數學習的興趣

教師要巧妙的設計課堂引入，充分調動學生學習的積極性。靈活設計和實際生活有關的學生感興趣的話題，并以此激發學生的求知欲。在教學中以學生為主體，老師進行指導。使學習者在克服困難，解決了函數的問題之后，能從中得到某種快樂，并感受到了自身的價值。敢于發表自己的想法，敢于質疑，通過體會小組合作的力量，養成良好的學習習慣。

二.要重視函數概念的教學

函數就是刻畫變量間對應關系的數學模型。在很多題目中，變量間的關系都可以用函數來描述。在課堂教學時，要讓學生體會函數思想的重要性。因此，使學習者切實了解函數知識，從實際問題中引入。如在某個變化過程中，有未知數x發生變化，對應y的數值就必然變化了，這二種未知量間的變化關系有一定的規律性，且具有唯一的對應性，可以用含未知數x的代數式表示未知數y，則稱x為自變量，y是x的函數。二者之間具有特殊的數量關系，這樣就將二元一次方程轉化為函數問題。學生也能類比日常生活中簡單的實例、學過的公式來加深對函數概念的理解。

三、以函數方法或思想為教學目標

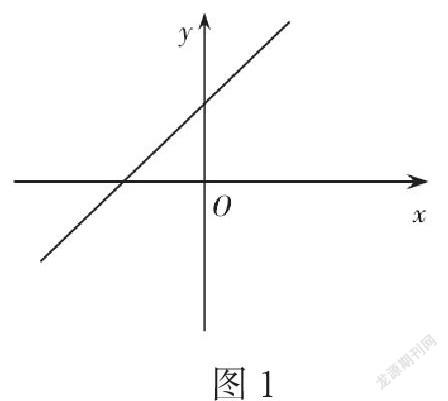
數學教學的最終目標是培養學生的數學思維，讓學生能夠掌握并運用基本的數學思想方法解決問題。函數中包含許多數學思想方法，如方程思想、類比思想、數形結合思想等。教師在教學中要滲透這些思想方法，讓學生逐漸領會并能夠將它們應用于數學學習中。例如在講解函數與方程時，教師可以從數與形兩個角度來講解。首先從數的角度對方程 x+3=0、函數y=x+3、不等式 x+3>0 的關系進行分析，學生通過邏輯分析很容易厘清方程與函數的關系，即當函數的 y=0時，就是方程 x+3=0;同時也能夠有效建立方程與不等式的關系，即當方程的“=”轉換成“>”時就得到了不等式。那么函數與不等式之間要如何聯系起來呢？教師可以引導學生用“形”的角度來分析 （見圖1）。

由圖 1 可知，函數圖象與橫軸相交的點就是方程x+3=0的解，圖象與橫軸交點的右半邊就是不等式x+3>0的解。函數實際上代表的是運動變化的軌跡，方程則可以看作為這一運動變化的某個瞬間，而不等式就是該運動軌跡中的某一段。教師通過將數形結合思想、轉化思想與函數教學聯系起來，促使學生進一步理解函數思想，同時也體會到了數學思想在數學學習中的意義。

四.注意各類函數間的聯系

函數是一個整體，各個具體函數是函數的特例。其中二次函數學起來最難，圖像復雜，從實際問題轉化為函數問題，然后利用圖象進行分析結論。最好再回到實際問題。讓學生感受學為所用。在教學上可類比一次函數、反比例函數的一些學習方法。如用待定系數法求解析式，理解了每一類型函數的概念，根據他們不同的表達形式，正確運用相應的函數模型，進而求出相應的函數解析式。在教學中要注意培養學生的數學思維，進行循序漸進的引導。教師一定要熟知教材，依據課標要求選擇合適的教學方法。例如，在二次函數的教學，教師可采用公式、圖形、函數意義多形式，比較一般式，頂點式，交點式這三種類型，掌握每一種形式的特征性質，圖形的平移規律，從而加深學生對二次函數的理解和應用。

五.利用多媒體輔助教學促進初中函數教學的形象化

在函數教學中，老師感到講的累，學生感到學的難，尤其對函數圖像及其性質等方面都存在一定的問題。采用多媒體輔助教學，可使學生直觀的觀察，能深刻的理解函數的增減性，體會一個變量隨著另一個變量是怎樣變化的。多媒體教學要與傳統教學有機結合，把抽象的理論知識具體化，發揮多媒體的優勢，將圖形運動變化過程模擬演示，從而使信息直觀和具體。但教師也要注意多走到學生當中，多交流，指導學生動手描點畫圖，顧全全體學生，使多媒體教學更有效地發揮作用。

六.加強后進生的輔導

面對學習層次不同的學生，教師要因材施教。做好小組學習分工，學生間要形成比、趕、超、越的良好學習風氣，同時教師要做好幫扶指導。正確的評價，充分調動學生學習的自主性，由學會到會學，不斷提升學習實效。

七.建立函數知識網絡，幫助學生學習函數

函數的根本是對不同變量之間的關系問題進行妥善處理，簡單而言，函數是法則之一，其讓每個變量之間都有一定的關系，可以是直接的，也可以是間接的，所以如果不能正確理解函數知識，容易導致函數中變量之間的關系十分混亂。學生不能全方位理解函數知識，也是造成解題錯誤的關鍵原因，所以必須建立完善的函數知識網絡，將不同知識點之間的關系理順。建立知識網絡必須從基礎知識開始，比如，初一數學教材中函數最開始講解的是函數定義，進而引出各種函數模型，接著是函數表達方式、圖象、表格和解析式，最后講解關于平面直角坐標系的運用，以上這些都有助于學生將來的函數學習。

結束語

總之，函數知識既是初中數學教學的重點，又是學生學習的難點。在教學中，教師要加強引導，由淺入深，循序漸進，加深學生對函數的理解和認識。多與生活實際的相聯系，使學生不再談函數"色變"，為進一步學習打下良好的學習基礎。

參考文獻

[1]劉海波.初中數學函數教學存在的困難及教學對策研究[J].求知導刊，2020（29）：30-61.

[2]曹艷芹.數形結合思想在初中函數學習中的應用研究[D].延安大學，2020

[3]向征.基于學為中心的初中數學函數精準教學探究[J].中學課程輔導（教師教j6CB78FA8-9337-4556-8CCC-141514E06CE1