函數圖像在高中數學解題中的應用

卓柳珊

[摘 要]函數在高中數學中占有重要的地位。函數圖像可以把立體空間與數量關系進行巧妙結合，學生通過觀察思考函數圖像常可獲得解決問題的方法。文章對函數圖像在高中數學解題中的具體應用進行探究，以期為一線教師的實際教學提供參考。

[關鍵詞]函數圖像;高中數學;解題

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2022）08-0032-03

數學解題和函數圖像之間有著微妙的聯系，多數情況下，函數圖像可以把立體空間與數量關系進行巧妙結合，而學生在觀察思考函數圖像的過程中常可獲得解決問題的方法。在高中數學教學中，教師需教會學生應用函數圖像，借此提升學生的解題效率和解題能力。本文主要對函數圖像在高中數學解題中的具體應用進行探究。

一、函數圖像簡述

函數是高考數學的必考點。函數涉及單調性、奇偶性、最值、零點、圖像等內容，函數圖像是函數學習的基礎，應用函數圖像可以對函數的單調性、奇偶性、值域等問題進行研究，所以學生應當深入學習，全面掌握函數的圖像與性質。對于函數圖像的繪制，可先看是否是基本初等函數，如果是，就可以直接繪制圖像;若非基本初等函數，則要看是否可以對函數進行一系列變換，比如翻折變換、對稱變換、伸縮變換、平移變換等，若可以，就可根據變換規律作出圖像。若無法進行變換，此類函數通常不作圖像繪制要求，相關題目大多是選擇題，只需計算得數，從選項中選擇答案即可。

二、基礎函數圖像分析

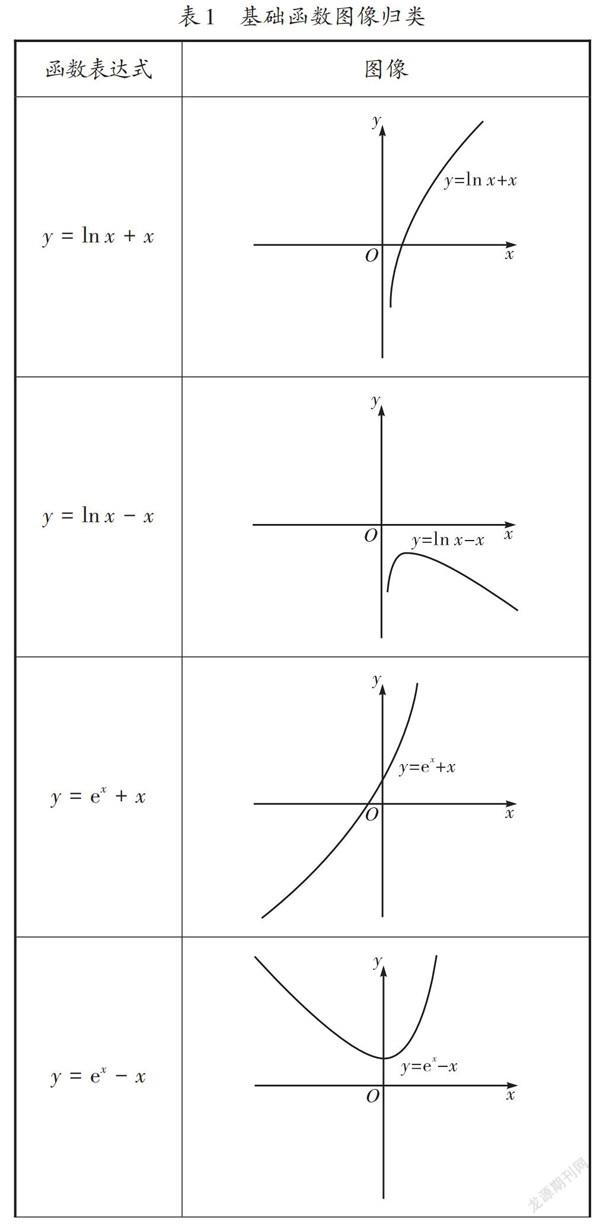
高中數學函數知識大多是以螺旋上升的形式呈現的，學生在學習時可由簡入繁、由淺入深，為此教師首先要讓學生掌握基礎的函數圖像。對于基礎函數圖像，學生若可以深刻記憶，則能夠有效促進函數圖像相關知識的學習，對解題也大有裨益。教師在日常教學中可以將一些基礎函數圖像或特殊組合函數圖像進行歸類總結（如表1），并以圖片、表格的形式呈現，方便學生記憶，避免學生產生混淆。

表1列舉的只是一部分基礎函數圖像，而高中數學中的基礎函數圖像有幾十種，為了使學生在記憶時避免產生混淆，教師在歸納整理時既要凸顯出各個函數圖像的特點，又要注意方式、方法的趣味性，使學生對函數圖像及相關知識印象深刻。

除此之外，教師還可以將各個函數圖像的變換方式錄制成視頻，并上傳至校園網，讓學生隨時隨地可以下載學習。

三、函數圖像的重要性

函數[f]的圖形（或圖像）指的是數學中所有有序對[（x， f（x））]組成的集合，它是學生重點學習的內容。函數圖像大多以曲線的形式體現在平面直角坐標系內，對學生解決函數問題有很大的幫助。初中數學知識分類較為明晰，代數、幾何知識的體現形式也比較直觀，但高中代數與幾何知識的分界不夠明晰，有時同一知識點既涉及代數，又涉及幾何。這不論是對教師的教學，還是對學生的學習都增加了難度。高考數學的分數分布比較細致，函數、導數知識占比30%，立體幾何占比12%，解析幾何占比15%，概率統計占比12%，而平面向量、三角函數、數列等知識，既自成體系又相互關聯，也是學生的得分所在。基于此，合理應用函數圖像，不僅可以幫助學生有效解題，還能幫助學生在考試中拿到更多的分數。由此可見，函數圖像的重要性不言而喻。

四、函數圖像在高中數學解題中的應用

（一）解答不等式及不等式組問題

不等式與函數存在緊密關聯，一般來說，在求解不等式類問題時，經常會用到函數圖像。函數圖像可以使問題直觀化，有助于學生解決問題。

[例1]求不等式[16-x2+8x-x2>4]的解集。

解：對原不等式進行變形，可得[16-x2>4-8x-x2]，再令[y1=16-x2]，[y2=4-8x-x2]，二次變形以上不等式，可得[x2+y21=] [16（y1≥0）]，[（x-4）2+（y2-4）2=16（y2≤4）]。

通過觀察，可以看出兩個函數的圖像全都是半圓，可以在同一直角坐標系中將其表示出來（如圖1）。由圖1可直觀、清晰地看到兩個半圓之間形成的交集，即原不等式對應的解集，也就是[x0<x<4]。

（二）指定區間判斷方程根的實根個數

方程與函數也存在緊密關聯，對于求方程實根個數類問題，可以先將方程轉化成相應函數，然后畫出函數的圖像，這樣可以直觀獲得問題答案。

[例2]方程[x13=2sinx]有? ? ? ? ? 個實根。

解：已知函數[y=x13]與函數[y=2sinx]都是奇函數，并且函數[y=x13]為增函數。

當[x=0]時，兩函數值都為0;

當[x=18]時，[1813=12>2×18>2sin18];

當[x=5π2]時，[2sin5π2=2]，[5π213<813=2];

當[x>8]時，[x13>2≥2sinx]。

由此，可畫出函數[y=x13]與函數[y=2sinx]在[x∈0， 3π]上的圖像，如圖2所示。

由圖2可知，函數[y=x13]與函數[y=2sinx]在[0， 3π]內的交點個數為4。因為函數[y=x13]與函數[y=2sinx]都是奇函數，所以在[-3π， 0]上也有4個交點，再加上原點，所以方程[x13=2sinx]的實數根的個數是9。

（三）解答復數問題

通過復平面上兩點之間對應的距離公式以及直線、圓、圓錐曲線等圖像，再借助復數的幾何意義對問題進行求解，遠比單純的代數運算要簡捷得多。

[例3]復數[z]滿足[z+i+z-i=2]，那么[z+i+1]的最小值是（ ）。

A. 1? ? ? ?B. [2]? ? ? ?C. 2? ? ? ? D. [5]

解：復平面內滿足[z+i+z-i=2]的點[z]的軌跡為[AB]線段，而[z+i+1]表示點[z]到點[P（-1，-1）]間的距離，如圖3所示。由圖知[z+i+1]的最小值是1，答案選A。

（四）解答解析幾何綜合類問題

在解答解析幾何綜合類問題時，經常會涉及函數圖像。這類問題的綜合性非常強，學生需結合函數圖像對問題展開分析，這樣才能有效解決問題。

[例4]已知曲線[y=1+4-x2]與直線[y=k（x-2）+4]存在兩個不同交點，求[k]的取值范圍。

解：將曲線[y=1+4-x2]適當變形，可得[x2+（y-1）2=4（1≤y≤3）]，這樣可以知道曲線[y=1+4-x2]是以[A（0， 1）]為圓心，以2為半徑的圓。但是題設當中存在一個隱含條件，即[y≥1]，所以圖像只有上半圓（如圖4）。

而直線[y=k（x-2）+4]是過點[B（2， 4）]的，當直線[y=k（x-2）+4]繞著點[B]進行順時針旋轉時，直線和圓相交的點保持在弧線[MT]上（點[T]除外）即可滿足題設要求。

又因為交點[M]位于直線[y=1]之上，所以能夠得到點[M]的坐標[（-2， 1）]。

而直線[BM]的斜率能夠用斜率公式求得，即[kMB=34]，而[M]點到點[A]的距離與圓的半徑相等，可以列出等式[1+2k-41+k2=2]，解得[kBT=512]，所以可得[512<k≤34]。

高中數學與初中數學不同，難度更大，涉及面更廣，對學生的要求也更高。不僅要求學生要具備邏輯思維，還要有較強的空間思維能力，并可以將所學的知識相互關聯，實現知識的整合。數學在高考中分數占比很大，學生只有具備較強的解題能力，才能確保在高考中獲得更多的分數。在日常教學中，教師除了幫助學生積累基礎知識，還應當強化學生的解題能力，同時幫助學生掌握有效的解題方法。

在高中數學解題當中函數圖像有著廣泛的應用，通過函數圖像的應用可以有效提高學生的解題效率和解題能力。為此，數學教師在教學中需引導學生深入了解函數圖像，并且傳授給學生函數圖像的應用方法，讓學生掌握各類函數的基本性質，充分理解一些函數模型，從而有效提升學生的解題效率和解題能力。

[? ?參? ?考? ?文? ?獻? ?]

[1]? 王洪民.輔助函數法及其在高中數學解題中的應用[J].中學生數理化（學習研究），2019（6）：16-17.

[2]? 許福生.函數與方程思想在高中數學解題中的應用[J].家長，2019（11）：148，150.

[3]? 李帥.由一道試題談函數模型在高中數學解題中的應用：淺談“對勾函數”的性質[J].中學生數理化（學習研究），2019（4）：14.

（責任編輯 黃春香）