小學數學高段“數與代數”領域中RMI原則的運用

江晨

【摘要】數學教學中關系映射反演原則是非常重要的數學思想，通過反演思維能夠把復雜問題映射到簡單問題中，從而達到化繁為簡、化難為易的目的。它在“數與代數”領域中應用廣泛，在數的運算、概念教學、解決問題中都起到培養學生邏輯思維能力，提高學生分析問題和解決問題的能力。

【關鍵詞】RMI原則;數與代數;小學數學

RMI原則是一種實用的數學原則，它是巧妙的把需要解決的復雜問題轉化為較簡單或者好理解的問題，從而達到解決原來問題的目的。簡單來說就是通過問題到問題的映射，從而得到化繁為簡，化難為易的目的。可以用思維圖來說明如下：

一、RMI原則在小學“數與代數”中的必然性和必要性

在小學數學“數與代數”領域中，存在大量的數的運算的學習。可是現如今雖然從小學一年級開始就在著重培養學生的運算方法，提高學生分析、解決問題的能力，但是到高段之后，依舊存在部分學生計算能力弱，對于復雜問題手足無措的現象。原因可能來自于老師上課形式、教學模式沒有起到很好的引導作用。我們對于數與代數領域的教學常常依賴于給學生大量的題型積累，多做多練，達到運算熟練。但這種方法導致學生只重視計算結果，只會做單調題型的計算，對于運算法則和原理了解的不夠透徹。課上可能對于算理的分析描述不夠，只講究算法的多樣性[]。

而學習數學不能單單學習數學知識，更要了解知識之間的聯系，學習數學的精神、思想和方法。數學知識并不是單一沒有邏輯的，而是呈網狀向外發散，并處處連接、層層遞進。在教學的過程中，教師要注重知識的上下承接，新舊聯系[]。

RMI原則能夠幫助學生養成良好的學習習慣和常態，在學習初期就從片狀式知識轉為線狀式知識。更好的理解掌握并且連接已學習的知識脈絡，發現數學知識在生活中的廣泛應用，感受學習數學的魅力和興趣。并且RMI原則能夠幫助學生更好的進行分析和處理問題，并培養學生解決問題的方法和策略。

二、概念映射：巧變素材，具化思維

數學概念作為數學知識的思維體現形式，是數學教學中非常重要的一塊。能夠正確理解靈活運動數學概念，也是掌握數學知識技能，發展數學思維邏輯的大前提。但對于從具體形象思維到抽象思維高速發展的小學生來說，數學概念是不太好理解，是抽象的。很多學生往往通過記憶背誦概念的形式來學習知識，效果往往事倍功半。

（一）概念喚醒，純化意義

【課例】5年級下冊的第4單元——《分數的意義》

對于單位“1”的定義通過一個小游戲引入

師：游戲名字就叫做“用1說話”。你們準備好了嗎？

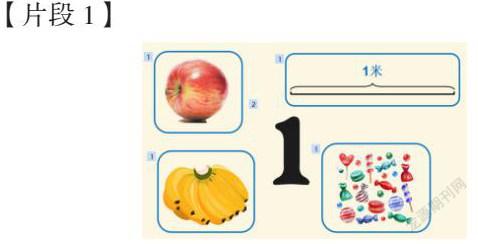
預設：1個圓;1條線段/一個計量單位;1個菠蘿;4個蘋果/一堆蘋果/一些蘋果（用圓圈圈起來）

【分析】

在之前的數學學習中沒有提過單位“1”的含義，而五年級開始把可以看作一個整體的物體叫做單位“1”，在這節課中要讓學生進一步體會、領悟單位“1”，為什么存在單位“1”。所以重難點在于是對單位“1”的理解。運用RMI原則，把單位“1”的概念映射到現實存在和學過的事物，由此來確定單位“1”的含義。

分數的意義的概念展示

【分析】

在教材中為了幫助學生能夠充分建立起分數的概念，通過這樣兩幅圖片來展示分數的產生。這兩幅圖找到了分數的產生與現實生活的關系，因為需要測量更小的數據和分更小的量，當不能用整數來代表的時候，為了更準確的表示了所需要的結果，于是需要分數[]。把抽象的分數巧妙的映射到現實情境中來，讓它有了實際的意義。

【課例】六年級上冊第六單元《百分數的認識》

百分數的產生

師：在之前的籃球比賽中，我們班同學奮勇拼搏，戰果累累。這是我們班三位主力平時的投籃練習情況。（出示三位學生的投籃總投球數和投中數）如果要出一名同學加入學校的校隊，該怎么選擇呢？

預設：比較他們的命中率，誰的命中率高選擇誰。

師：那該怎么比較呢？

預設：計算每次投籃中，投中的數量占總數量的幾分之幾。

師：請4人為一小組，算一算誰的投中率比較高。想一想有沒有什么好辦法能夠直接來比較他們的大小？

小組討論，動手計算比較。引導學生將三個分數通分成分母是100的分數，并由此引出百分數的概念。

【分析】

百分數這個詞對學生來說比較陌生，所以在這里創設情境，從學生已有的分數的知識基礎上，加以映射，從而根據分數的意義順理成章的引入百分數。也為之后分數、整數和小數的互換打下基礎。

（三）概念提升，拓展廣度

【課例】師：生活中有很多百分數，你還在什么地方見過？

展示學生搜集到的含有百分數的句子，并說說百分數的含義。

例如：小學生的近視率為18%。就是說小學生中近視的人數占全體小學生人數的。

初中生的近視率為49%。也就是初中生的近視學生是全部初中學生數量的。

【分析】

三、運算映射：巧聯舊知，勾連思維

（一）數數相對，找準關系

如小數乘法3.1×20，可以先讓學生利用整數乘法的31×20，得出答案620。再找到積的小數點和兩個乘數的小數點的關系，確定積是幾位小數。這種方法能夠幫助學生快速理解小數乘法如何運算，并且能夠運算的又快又對。其實這也是教材推薦的方式，把抽象難懂小數運算的變成熟悉的整數乘法。

在RMI原則中，重要的是找準新知與舊知之間的對應關系，確定好可以映射的對象，映射可以一步也可以幾步進行，重點在于把學生不好理解的問題簡單化，化為學生已學過熟悉的事物和知識，再反演得出答案。

四、RMI原則后續思考

RMI原則作為一種分析處理問題的重要方法，不止在小學階段，在之后初中、高中甚至高等數學的學習中都起到非常重要的作用。運用RMI原則選取合適的映射，能夠拓展學生的解題思路，降低解決問題的難度。所以，教師在教學過程中，要有意思的聯系小學數學的知識體系，鼓勵倡導學生利用RMI原則挖掘數學問題的本質信息來解決問題。這能夠幫助學生提高數學解題的思想層次，樂于發現數學問題中的核心價值，愿意去探索、歸納、總結。

參考文獻：

[1]劉大衛.“RMI”數學思想及其應用初探[M].成陽：成陽師范專科學校學報 （ 自然科學版 ），1998.

[2]戴祥領.RML方法在數學中的應用[M].貴州：遵義師范學院學報，2004.