構造相似三角形解題例談
劉曉玲

【摘要】數學課是中學課程教育的核心課程,在整個初中乃至高中都十分重要.教育者應該注重培養學生的數學思維,引導學生在日常生活中養成良好的學習習慣,可以有效提高學生的解題質量及效率.本文以蘇教版“相似三角形”為例,提升學生對相似三角形的認知,也能提升學生數學能力的培養.
【關鍵詞】初中數學;構造相似三角形;解題方法
數學在日常生活中作用越來越明顯,更加體現出數學的優勢,教育者應該注重對學生數學思維和數學能力的培養[1-2].初中是中小學以及普高的過渡期,在一定程度上難度加大,不再是簡單的四則運算,這也就更加體現出學習數學的重要性[3].相似三角形作為初中學習架構中關鍵性的一環,對于中考來說也是重要的考點和難點.因此,探究相似三角形的方法以及形成一定的數學知識的架構對于學生來說非常重要.
1 初中數學構造相似三角形學習方法
相似三角形是初中幾何中的重要內容,常常與其他知識點結合,以綜合題的形式呈現,變化很多,是中考中的常考題型.如果我們注重解題方法或基本解題模型,相信再遇到相似三角形的問題就迎刃而解了.下面就介紹一下相似三角形模型.
1.1 相似三角形中的 A字模型
例1 如,在△ABC中,AB=8cm,AC=16cm,其中,點P以2cm/s的速度從A點向B點運動,同時,點Q以3cm/s的速度從C點向A運動,一旦P或者Q點任意一點在t時間達到至B或者A時,另外一點也隨之停止.如何用t表征代數式AP和AQ;時間t為多少時,△APQ∽△ABC.
解題思路 本題主要是考查相似三角形的判定定理,可以靈活變通,熟練掌握數學解題思路.
即:兩組對應邊的比相等且夾角對應相等的兩個三角形相似.
對于第一問來說,主要是采用速度公式求解;利用相似定理(∠PAQ=∠BAC),當APAB=AQAC時,則有△APQ∽△ABC,與之相對應的有:2t8=16-3t16
;當APAC=AQAB時,則有△APQ∽△ABC,與之相對應的有:2t16=16-3t8,利用相似性進行計算求解.
解題過程 (1)首先看點運動的方向,P點從A點出發,利用速度公式可以得到AP=2t;
而AQ的長度為未經過的長度,已知AC=16cm,則有AQ=16-3t.
(2)連接PQ,見圖2.
因為∠PAQ=∠BAC,
所以當APAB=AQAC時,△APQ∽△ABC,此時2t8=16-3t16,解得t=167;
因為∠PAQ=∠BAC,
所以當APAC=AQAB
時,△APQ∽△ACB,此時2t16=16-3t8,解得t=4.
所以運動時間為167s或4s.
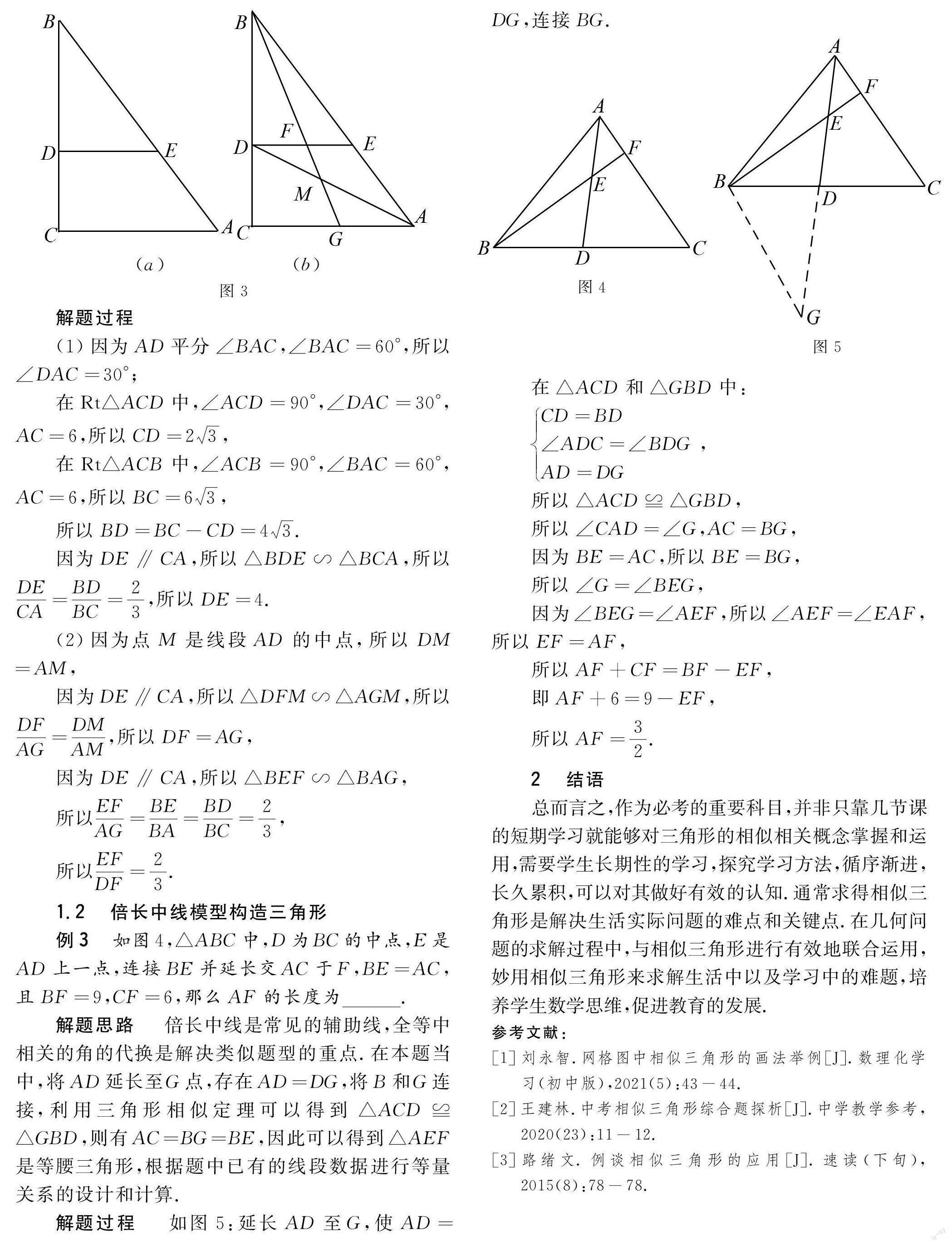
例2 如圖3(a)和圖3(b),在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,在Rt△ABC中的BC邊上交于點D,此時過點D做CA邊的平行線,在Rt△ABC中的AB
邊上交于點E.此時,求DE的長,線段AD的中點為M,連接B、M兩點,與DE于點F,將BM延長邊AC于點G,求解EFDF的值.
解題思路 本題考查了相似三角形的判定,關鍵是能靈活運用.
(a)?????? (b)
解題過程
(1)因為AD平分∠BAC,∠BAC=60°,所以∠DAC=30°;
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,所以CD=23,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,所以BC=63,
所以BD=BC-CD=43.
因為DE∥CA,所以△BDE∽△BCA,所以DECA=BDBC=23,所以DE=4.
(2)因為點M是線段AD的中點,所以DM=AM,
因為DE∥CA,所以△DFM∽△AGM,所以DFAG=DMAM,所以DF=AG,
因為DE∥CA,所以△BEF∽△BAG,
所以EFAG=BEBA=BDBC=23,
所以EFDF=23.
1.2 倍長中線模型構造三角形
例3 如圖4,△ABC中,D為BC的中點,E是AD上一點,連接BE并延長交AC于F,BE=AC,且BF=9,CF=6,那么AF的長度為.
解題思路 倍長中線是常見的輔助線,全等中相關的角的代換是解決類似題型的重點.在本題當中,將AD延長至G點,存在AD=DG,將B和G連接,利用三角形相似定理可以得到△ACD≌△GBD,則有AC=BG=BE,因此可以得到△AEF是等腰三角形,根據題中已有的線段數據進行等量關系的設計和計算.
解題過程 如圖5:延長AD至G,使AD=DG,連接BG.
在△ACD和△GBD中:
CD=BD∠ADC=∠BDGAD=DG ,
所以△ACD≌△GBD,
所以∠CAD=∠G,AC=BG,
因為BE=AC,所以BE=BG,
所以∠G=∠BEG,
因為∠BEG=∠AEF,所以∠AEF=∠EAF,所以EF=AF,
所以AF+CF=BF-EF,
即AF+6=9-EF,
所以AF=32.
2 結語
總而言之,作為必考的重要科目,并非只靠幾節課的短期學習就能夠對三角形的相似相關概念掌握和運用,需要學生長期性的學習,探究學習方法,循序漸進,長久累積,可以對其做好有效的認知.通常求得相似三角形是解決生活實際問題的難點和關鍵點.在幾何問題的求解過程中,與相似三角形進行有效地聯合運用,妙用相似三角形來求解生活中以及學習中的難題,培養學生數學思維,促進教育的發展.
參考文獻:
[1]劉永智.網格圖中相似三角形的畫法舉例[J].數理化學習(初中版),2021(5):43-44.
[2]王建林.中考相似三角形綜合題探析[J].中學教學參考,2020(23):11-12.
[3]路緒文.例談相似三角形的應用[J].速讀(下旬),2015(8):78-78.

