高中數學核心素養下的問題式教學案例

劉俊蓉 楊秋 明慶

摘要：現高中數學的六大核心素養：數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析，這六大核心素養既相互獨立，又相互交融，共同構成了學生的數學綜合能力。是學生學習數學的基本思維品質、關鍵能力以及情感、態度、價值觀的綜合體現。需要教師在教學過程中積極探索合適的教學方法，培養學生的核心素養。在當前時代背景下，學生核心素養的培養受到了高度的重視，如何在常態教學中植入六大核心素養的培養，是教師教學中的重點、也是教學的難點。核心素養的形成過程就是學生的數學思維的建立和數學綜合能力的培養過程。所以常態教學課中教學路徑的探究就成了我們的一個重要課題，問題式教學路徑是老師們在日常教學中采用的一種常用的教學方法。

關鍵詞：高中數學、核心素養、培養、教學路徑、問題式

一、教學案例

（一）授課對象與方法

本節課的授課對象是四川省廣安友誼中學高一學生。該校是一所省級示范校，一本升學率可達到50%，學生基礎在廣安市相對較好。授課內容是普通高中教科書《數學》必修 第一冊（A版）第三章3.1.1《函數概念》第一課時。主要采用問題串式教學法。

（二）教學設計

1.新知導入

初中的定義中，函數是刻畫變量之間對應關系的數學模型和工具.

例：正方形的周長 l與邊長 x的對應關系

思考：（1）l是x的函數嗎？

x∈R? y=1，y是 x的函數嗎？

2.新知探究

問題1? 某“復興號”高速列車加速到350 km/h后保持勻速運行半小時.

思考：（1）列車行進的路程S與運行時間t 的關系是什么？

（2）有人說：“這趟列車加速到350 km/h后，運行1 h就前進了350 km.”你認為這個說法正確嗎？

問題2? ?某電氣維修公司要求工人每周工作至少1天，至多不超過6天.如果公司確定的工資標準是每人每天350元，而且每周付一次工資.

思考： 工資w（單位：元） 與工作天數d 的關系是什么？

問題3? 如圖1是北京市2016年11月23日的空氣質量指數（Air Quality Index，簡稱AQI）變化圖.

圖1 北京市2016年11月23日AQI變化圖

探究 ：請你仿照問題1和問題2，用兩個集合和一種關系描述問題3.

問題4 由上述三個問題抽象出來的數量關系有哪些共同特征？

① 都包含兩個非空數集，用A、B來表示;

② 都有一個對應關系;

③ 對于數集A中的任意一個數 x，按照對應關系，在數集B中都有唯一確定的數 y 和它對應.

對應關系除了我們熟悉的函數表達式，還可以是圖像、表格等。

為了表示方便，我們引進符號 f 統一表示對應關系。

函數概念：? 一般地，設A，B是非空的實數集，如果對于集合A中的任意一個數 x，按照某種確定的對應關系 f，在集合B 中都有唯一確定的數 y和它對應，那么就稱 f：A→B為從集合A到集合B的一個函數，記作y=f（x），x∈A.

其中，x叫作自變量，x的取值范圍A叫作函數的定義域;與x的值相對應的 y值叫作函數值，函數值的集合{f（x）|x∈A}叫作函數的值域.

概念剖析：（1）構成函數的三要素

（2）值域與集合B的關系

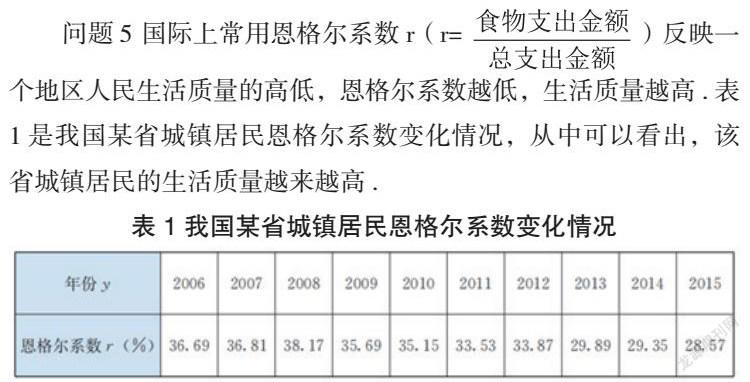
問題5 國際上常用恩格爾系數r（r=）反映一個地區人民生活質量的高低，恩格爾系數越低，生活質量越高.表1是我國某省城鎮居民恩格爾系數變化情況，從中可以看出，該省城鎮居民的生活質量越來越高.

表1 我國某省城鎮居民恩格爾系數變化情況

探究 ：按表1給出的對應關系，恩格爾系數r 是年份y 的函數嗎？為什么？

3.典例分析

搶答題：（1）判斷下列對應關系是否是函數.

①A={平面M內的三角形}，B={平面M內的圓}，f：畫三角形的外接圓;

②A=R，B={x|x>0}，f：x→y=|x|;

③A={x|-1≤x≤1}，B={1}，f：x→y=1.

④下列圖形中不能構成函數y=f（x），x∈A.的圖像的是（ ）

搶答題： （2）下列哪些函數與 y = x 表示同一函數？

①; ②; ③; ④

思考： y=2x2-x+1? 與? y=2t2-t+1 是否為同一函數？

二、案例分析

問題式教學：是以提出問題、分析問題、解決問題為線索，并把這一線索始終貫穿整個教學過程。也就是教師先設計好問題，學生帶著問題進入課堂，通過理解問題，討論問題，針對性地解決問題。這種教學法操作方便，適合高中生，實踐效果良好。在問題式教學中問題的質量是關鍵，問題之間要有邏輯關系，要切中要害，引起學生的興趣。

本節課在短短的40分鐘課堂內，要讓學生經歷函數定義發展史上百年的探究歷程，學生不可能獨立完成。這需要教師用材料鋪好一條路，要了解學情，并對學生的疑問做好預測，難度大的地方搭好梯子。本節課以學生為主體，教師引導教學原則來設計，著重解決了學生的幾個疑問：

（一）引發認知沖突

初中定義中，函數是刻畫變量之間對應關系的數學模型和工具.

例如，正方形的周長 l與邊長 x的對應關系? ?l=4x.

思考：（1）l是x的函數嗎？

（2）x∈R? y=1，y是 x的函數嗎？

通過回憶舊知，引出困惑

用快剪輯制作短視頻《函數概念的發展史》，激發學生的學習沖動和學習熱情.

（二）概念的生成

高一學生的抽象概括能力還很薄弱，這使得用集合語言刻畫函數概念很有難度。如果直接歸納定義，學生會失去剛剛燃起的探究欲望。所以選擇從情景問題1入手，引導學生關注時間t的變化范圍，跳出問題情境，抽象出數量關系，得出：兩個非空數集A、B及其之間的對應關系;緊接著，拋出情景問題2，用問題串引領學生完成實例2的分析，在分析過程中重點讓學生體會分析情境，輔助學生抽象出數量關系并進一步理解數量關系中的任意性、存在性、唯一性;接下來的情景問題3，學生根據圖像描述對應關系有困難，特別是在值域不能完全確定時，通過引入一個較大范用的集合，使函數值“落入其中”，這是學生經驗中不具備的，由老師規范表述，進一步強化數量關系中的任意性、存在性、唯一性。

學生通過歸納三個情景問題的共同特征，體會數學抽象過程，概括出用集合與對應語言刻畫的一般性函數概念.讓學生進行歸納、概括、抽象出函數概念，并以此培養學生的數學“抽象素養”這一難點。

通過創設情境，形成概念。尤其注重了概念的自然生成。從特殊到一般，揭示數學通常的發現過程，給學生“數學創造”的體驗。這種引入概念的方式自然而又易于學生接受和形成概念

（三）概念的理解

引導學生從函數概念的內涵、要素的歸納過程，關鍵詞的理解等角度進行小結，進一步加深對函數槪念的理解。

利用已有概念，判斷情境問題5是否構成函數，并體會以表格形式呈現的對應關系。

（四）概念的應用

新課引入，概念生成，到這個時候已經上課快30分鐘，學生注意力，精神狀態都略顯不足。此時，我以倒計時搶答題的形式增加課堂樂趣，鞏固新知。例1判斷下列對應關系是否是函數，進一步從任意性、存在性、唯一性這三性理解函數概念。其中③A={x|-1≤x≤1}，B={1}，f：x→y=1.回應了引入中（2）x∈R? y=1，y是 x的函數嗎？

例2 和相應的思考，有效的幫助學生進一步理解函數三要素，課外拓展設計以開放式角度訓練思維。

三、案例效果

本節課是一堂高效課堂。高效課堂是高效型課堂和高效性課堂的簡稱，是教育教學效率或效果達成了相當高的目標。具體而言是指在有效課堂的基礎上，完成了教學任務，達成了教學目標，效果較好并且取得了教育教學的較高影響力和社會效益的課堂，高效課堂是有效課堂的最高境界，高校課堂基于高效教學，與教學的設計和教師的能力有很大的關系。

這節課的設計思路清晰，課堂氣氛活躍，以游戲搶答的方式寓教于樂。問題的設置多樣化，有教是事先預設的問題鏈，也有學生主動提出的問題，同時還有問題的開放性，提升學生的思維。根據問題學生的學習目標明確，效果突出，很好地激發了學生的內在動力。40分鐘，學生理解并掌握了函數的內涵，本質。通過課堂習題反饋情況看，這節課起到較好的教學效果，大多數學生能獨立、正確地完成.

參考文獻：

[1]中華人民共和國教育部制定.普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2018.

[2]章建躍.第三章“函數的概念與性質”教材介紹與教學建議[J].中學數學教學參考（上旬），2019（28）：17-24.

[3]王克亮.高中數學教學“問題驅動”的探索與實踐[M].蘇州：蘇州大學出版社，2017.