初中物理解題中極限思維法的有效應用

時華夏

【摘要】在物理學發展歷程中，極限思維法始終占據著重要地位，現在已經成為一種常用的解題方法.在初中物理解題教學中，教師可指導學生有效應用極限思維法，使其發散思維，轉變固有的思維模式，能夠觸類旁通、舉一反三，讓他們學會運用極限思維法解答物理問題.筆者主要對初中物理解題教學中怎么應用極限思維法進行探討，同時列舉部分有效舉措.

【關鍵詞】初中物理;解題教學;極限思維

極限思維法即將復雜的物理過程進行分解，分解的小過程變化單一，因此，選擇整個過程的兩個端點和中間的極限對問題進行分析，在結果中包括物理過程討論，更加直觀、簡單的解答問題.初中物理教師在解題教學中指引學生有效應用極限思維法，讓他們迅速找到準確的解題思路以及方法，使其解題過程變得事半功倍.

1 利用極限思維法，找準問題入口

物理是學生在初中時期才接觸到的一門新科目，他們在處理物理題目時，往往無法讀懂題意，更是無法判定出各個數值在題干中所起到的作用，無法找到問題的入口.而且傳統的解題方式極易限制學生的思維，解題過程顯得程序化，難以找到快捷的解題方法，初中物理教師可指引他們利用極限思維法找準解題的切入點，使其在較短時間內就確定解題方法.

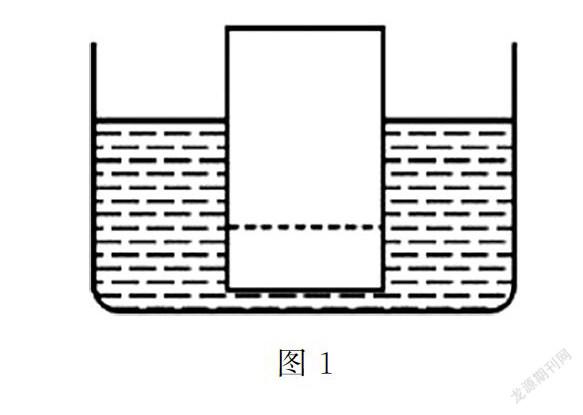
例1 在杯子中盛有半杯水，將一塊木塊放入其中，木塊上半塊浮出水面，沿著圖1中的虛線位置將木塊下部分截掉，那么剩余的木塊位置將會發生什么變化？[1]

解析 如果使用傳統的解題方式，學生將會考慮到木塊的密度是均勻的，無論是否將下半部分截掉，都一定會浮在水面上，不過當木板的下半部分被截掉以后，體積將會變小，受到的浮力同樣會變小，判斷出木板的位置同之前相比會有所下降.運用極限思維法時，學生可反向思考，根據題目中的要求，將木塊的下半部分截掉，木塊依然處于水中漂浮狀態，因為木塊自身密度沒有發生變化，導致木板仍然能夠在水中漂浮，因此，木塊下半部分也一定會浸泡在水中.在解題中，引導學生利用極限思維法，快速找到解題的切入點，以免出現計算數值的繁瑣，有效節省解題時間.

2 運用極限思維法，活躍學生思維

物理作為一門典型的自然科學類科目，學習這類課程知識時，最擔心的一個問題就是學生“鉆牛角尖”，思維陷入到瓶頸之中，出現固定不變的情況，甚至很難發生轉變，以至于他們無法順利學習.在初中物理解題教學中，教師應該采取多種方式調動學生的解題興趣，使其學會運用極限思維法來解題，讓他們思維變得活躍起來，在解題中表現得更為高效[2].

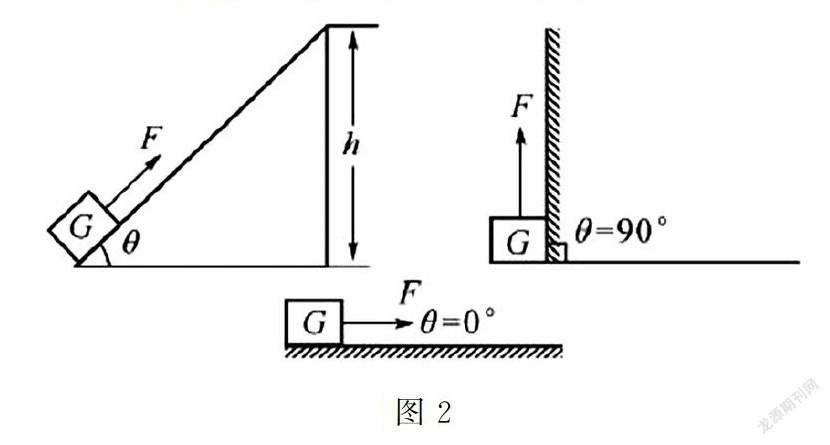
例2 如圖2所示，在平行斜面上向上拉一個物體，斜面機械效率受到哪些因素影響？

解析當把一個物體往斜面上拉時，一定會出現摩擦力，因此，需要做有用功，機械效率高低和額外功存在很大的關系，額外功越高，機械效率就會越低.同時，額外功的大小還同摩擦力存在聯系，大小和摩擦力基本相同，摩擦力的大小和物體壓力相同，同時和斜面的粗糙度有著直接聯系;物體壓力大小和斜面傾斜度大小有著聯系，傾斜面角度越大，物理壓力則越小.結合極限思維法進行分析，傾斜面的傾斜角度和機械效率相關，斜面角度越大，則壓力變小，當壓力變小后，物體對斜面的摩擦力會減小，摩擦力越小，則其額外功就越小，額外功越小，則其機械效率就會越高.因此，機械效率高低和物體壓力、斜面粗糙程度、傾斜度有著密切關系.

3 應用極限思維法，解決力學問題

力學整個物理知識體系的基礎，在初中物理解題教學中，不少力學問題中都會存在角度或者長度的變化，這個時候通常可以采用極限思維法來分析試題，考慮角度或者長度變化中區間端點的特殊情況.初中物理教師可指導學生把題中的數值、物理量的方向推向某一個極端值的狀態，降低力學問題難度，明確學生解題思路，使得解題思路更為簡化[3].

例3 在某一角度可變化的斜面上放置一個由細繩牽引的物體，質量是G，角度變化的范圍是0°—90°，在整個牽引過程中，保持物體處于靜止狀態，如果斜面的摩擦力足夠大，當傾斜角從0°增大至90°的過程中，物體受到的支撐力有著什么樣的變化？

解析不少學生認為，由于物體在斜面上處于靜止狀態，所以受到的支撐力有可能是不變的，教師可提醒他們分析題目中出現的變化量，即為斜面的角度，使其應用極限思維法，直接思考變化角度區間的兩種極限情況，也就是0°與90°的情況.

當斜面角度是0°時，物體承受的支撐力大熊和物體的重力相同，當傾斜角是90°時，物體承受的支撐力為零.因此，在整個變化中，物體始終保持靜止狀態，因此，物體受到和支撐力相同且相反的平衡力，變化過程保持其連續性，則物體所授支持力的變化范圍是0—G.

4 巧用極限思維法，解答運動問題

初中物理學習中，運動類題目是非常常見的題目，在問題解答中需要應用到極限思維法，在具體的使用中，應當引導學生對題目中的物理量進行梳理，并緊密結合實際生活，不能脫離基本事實與違背物理原理，使其根據具體解題需求確定好進行極限化處理的物理量，把運動學問題變得簡單易處理，提升他們的解題效率[4].

例4 甲、乙兩地之間有一條河流，其中甲位于上游，兩地之間的距離是s，現在有一艘小船從甲處行駛至乙處，速度是v，達到乙處以后立即向甲處返回，已知往返一次的時間是t，那么下列選項中表述正確的是（）

（A）t>2s/v（B）t=2s/v

（C）t<2s/v （D）上述情況均有可能.

解析 假如使用傳統解法，需考慮到船速與水速的合成，并結合路程列出計算式求解，過程顯得較為復雜，不適用于選擇題，而使用極限思維法處理這一運動類問題，就顯得沒有這么繁瑣.具體來說，本道題目中主要涉及到路程、水速與船速三個有關運動的物理量，學生采用極限思維法時，首先需考慮將哪一個物理量進行極限化處理，分析以后發現最恰當的是船速，當船逆流返回到甲處時，如果和水流的合成速度為零，那么船則無法返回，因此，返回的時間則是無限大的，即為本題的正確答案是選項（A）.

5 借助極限思維法，解答電學問題

初中物理課堂中，部分電學問題較為復雜，屬于難度相對較大的題目，要想更好地處理這類物理試題，需要加強課堂引導，利用電路圖的優勢，對問題進行分析，針對存在滑動變阻器等范圍變動的問題，應更為靈活地使用極限思維法，使其準確找到處理問題的區間，找出不同物理量在不同區間的極值，完成電學問題的思考和解答[5].

例5 將一個滑動變阻器和定值電阻串聯，構建成電路，其電壓是220V，互動變阻器的阻值范圍是0—100Ω，定值電阻為10Ω，在滑動變阻器的滑片移動中，電壓表的讀數范圍是多少？

解析 在處理這道電學類的題目時，學生應找到本題中出現的變化量，即為滑動變阻器的阻值大小，因為是一個變化的區間，所以運用極限思維法解題時，可以把滑動變阻器的兩個端點阻值大小當作計算依據，即為0Ω與100Ω.具體解答過程如下：運用極限思維法對滑動變阻器的阻值情況進行極限處理，當滑動變阻器接入電路的阻值是0Ω時，電路中電流最大，此時的定值電阻兩端電壓最大，即220V;當滑動變阻器的阻值是100Ω時，定值電阻兩端電壓值最小，即為20V，那么本題的正確結果就是定值電阻兩端所測定的電壓表讀數范圍在20V至220V之間.

6 采用極限思維法，解決壓強問題

壓強是一個表示壓力作用效果的物理量，指的是物體所受壓力的大小與受力面積之比，壓強越大，壓力的作用效果就越明顯.

在初中物理課程教學中，壓強也是一個比較重要的知識點，還是中考中的必考點之一，處理部分壓強類的問題時，教師引導學生利用極限思維法，對物體壓強做出分析，使其找準解題的突破口，幫助他們形成清晰的思路[6].

例6 在水平面上，放置有兩個不同高度的實心金屬圓柱體，兩個圓柱對地面壓強相同，從水平方向就能夠兩個實心金屬圓柱體截掉相同高度，兩個金屬圓柱體剩余部分對水平面的壓強有著怎樣的關系？

解析 在此題解答中，題目中并沒有明確給出實心金屬圓柱體的高度，同時，對圓柱體截取的高度也沒有提出，題目中的已知條件比較少，內容較為抽象，解答的難度比較大.

在解題中，如果讓學生采取傳統解題思路，需要利用壓強公式計算圓柱體密度的關系，截取高度相同，那么，密度較大的金屬圓柱體剩余部分產生的壓強較小，此種解題方式計算繁瑣，分析過程也比較復雜，很容易出現解題錯誤.

作為教師，引導學生利用極限思維法解題，將截取金屬圓柱體高度最大化，當截取的金屬圓柱體高度和較低圓柱體高度相同，那么較低實心圓柱體則就被完全截取，對水平面的壓強是零，另一個實心圓柱體依然有剩余，對地面壓強則不可能是零，通過這樣可以輕松解答題目，即可以得出較好實心圓柱體被截取后對水平面的壓強較大.

處理初中物理中的壓強類試題時，通常會涉及到高度變化問題，教師就需引領學生采用極限思維發，對最大長度展開考慮，并把握好長度區間的變化，把變化的物理量推向某一個極端，以此更好的判斷出物理量的值，提升他們的解題水平.

7 總結

在初中物理解題教學活動中，由于學生在初中階段才開始接觸物理學科，解題過程更為繁瑣，既要分析、又要計算，容易遇到思維障礙，很多時候甚至一頭霧水，不知道從何處下手，教師應多指導他們運用極限思維法處理題目，使其思維得以充分發散開來，學會進行逆向思考，繼而不斷提升自身的物理解題能力，同時掌握更多解答物理問題的技巧與方法.

參考文獻：

[1]凌習華.初中物理解題中的極限思維運用[J].數理化解題研究，2021（29）：83-84.

[2]胡慶霞.極限思維在初中物理解題中的融合[J].數理化解題研究，2020（08）：78-79.

[3]張曉芳.極限思維法在初中物理解題中的妙用[J].試題與研究，2019（30）：144.

[4]李花.探究極限思維在初中物理解題中的應用[J].數理化解題研究，2019（08）：45-46.

[5]杜云倫.極限思維在初中物理解題中的應用[J].數理化解題研究，2019（20）：58-59.

[6]徐紅偉.探討極限思維在初中物理解題中的應用[J].數理化解題研究，2019（17）：69-70.