以“學生提問”撬動深度學習

張齊華

摘要：鼓勵、引導學生提出問題，并且基于學生提問展開數學教學，有利于引發學生的深度學習。《軸對稱圖形》一課，以學生提問為支點，通過前置學習任務中的獨立提問、小組共同學習中的相互提問、全班組際對話中的互動答疑等學習活動，激發學生主動參與、充分卷入學習，撬動深度學習。

關鍵詞：小學數學；提出問題；學生提問；深度學習；《軸對稱圖形》

*本文系江蘇省教育科學“十四五”規劃課題“促進兒童社會性素養發展的‘社會化學習’范式建構”（批準號：SJMJ/2021/03）的階段性研究成果。

所謂“深度學習”，是指“在教師引領下，學生圍繞著具有挑戰性的學習主題，全身心積極參與、體驗成功、獲得發展的有意義的學習過程”［1］。鼓勵、引導學生提出問題，并且基于學生提問展開數學教學，是觸發學生深度學習的有效路徑。一方面，學生有價值的提問，往往發生在已知與未知的交界處，發生于“最近發展區”，對學生而言具有適切的思維挑戰，容易激發學生的好奇心和求知欲。另一方面，由于推動課堂前行的問題不再由教師主導，也并非來自教材、教參等課程文本，而是來源于學生自己。這樣的問題與學生息息相關，更容易引發學生的探究興趣和思考樂趣，激發學生的學習主動性。最后，當學生提出的問題經過獨立思考或同伴互助，最終由學生自己解決時，這樣的成功體驗是解決教師提出的問題所無法比擬和替代的。因而，由學生提問展開的數學學習就具備了深度學習的特質。

近幾年來，筆者帶領小學數學團隊開展的“社會化學習”課堂變革實踐，正是以“學習地圖”為載體，以“小組共學”為路徑，以“組際答疑”為核心，借助“學生提問”這一關鍵因子，通過“前置學習任務中的獨立提問”“小組共同學習中的相互提問”“全班組際對話中的互動答疑”這些連續性的學習活動，著力撬動課堂中學生的深度學習。本文介紹一個具體案例。

一、教學過程

（一）獨立探索，在深度研究中引發個體提問

師（出示學習單）課前，同學們獨立完成了這個學習單，提出了學習過程中屬于自己的問題。比如，有同學提出：“除了對折，還可以用什么更快捷的方法判斷一個圖形是不是軸對稱圖形？”有同學提出：“軸對稱圖形可以有兩條對稱軸嗎？”有同學提出：“學習軸對稱圖形有什么用？”……看得出來，大家在獨立研究的過程中，既形成了自己對軸對稱圖形的初步理解，也產生了很多新的困惑。在老師看來，這就是有意義的學習，也是有深度的學習。為大家“點贊”！

學習單的內容如下：

【我的目標】

1.能判斷日常生活中的對稱現象，通過折一折、剪一剪、比一比等活動，認識軸對稱圖形，認識對稱軸。

2.能通過看一看、折一折、比一比、想一想，判斷一個圖形是不是軸對稱圖形。

【我的研究】

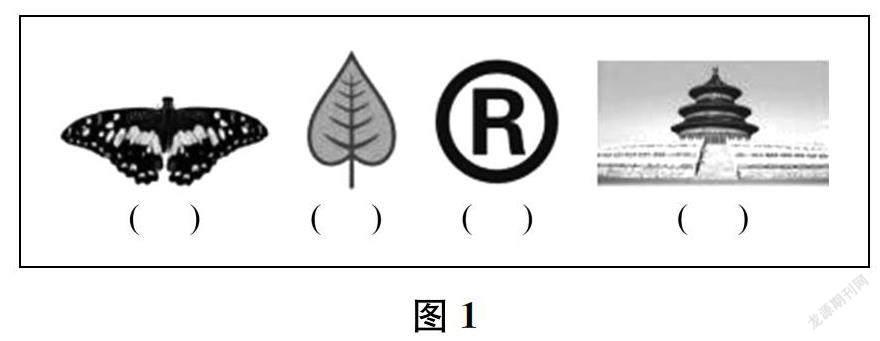
1.圖1中的哪些現象是“對稱”的？在（）里打“√”。

你是怎么判斷的？把你的想法寫下來。

2.把一張紙對折后，照樣子（如圖2）畫一畫、剪一剪。

（1）剪下的圖形是一個軸對稱圖形。對折時，折痕所在的線是它的對稱軸。

（2）你能像這樣，折一折、畫一畫、剪一剪，剪出3個不同的軸對稱圖形嗎？

記得把作品帶到課堂上來，和同伴說一說你是怎么剪的，它們的對稱軸在哪里。

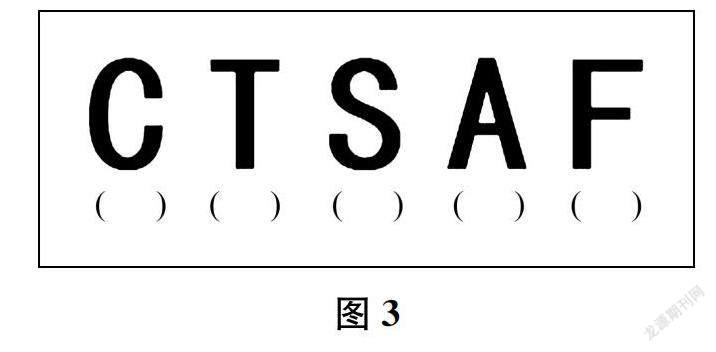
3.圖3中的五個字母，哪幾個是軸對稱圖形？在（）里打“√”，并說明理由。

4.關于今天的學習內容，你還能提出什么問題？

學習單給出了本節課基本的學習目標和指引學生完成學習目標（探索新知識、建構新理解、生成新經驗）的學習任務。學生在獨立完成學習單的過程中，由于經驗、思維與能力的不足，自然會產生認知失衡，也就能提出自己的問題。

（二）組內交流，在持續對話中生成小組提問

師接下來，請大家在小組中先分享自己的思考，再帶著自己的問題碰撞交流。組內解決不了的問題，或產生出的新問題，可以提交全班進行討論。

（學生小組交流，持續約15分鐘。教師巡視。）

一個四人學習小組的交流過程如下：

生（1號）今天，我們討論的內容是軸對稱圖形，我們先來看學習目標。（解讀學習目標）接下來，我們來看“我的研究”第1題的第一個圖形。誰來說？

生（4號）第一個圖形是軸對稱圖形。如果拿筆畫一畫，它的中間有一條對稱軸。

生（2號）大家還有別的方法來判斷嗎？

生（1號）如果把這只蝴蝶剪下來，對折一下，兩邊應該是一樣的，所以它是軸對稱圖形。

生（2號）我來總結一下：只要找到對稱軸，或者折一折兩邊重合，就可以認為這個圖形是軸對稱圖形。第二個圖形，誰來說？

生（1號）它是軸對稱圖形。把這片樹葉左右對折，兩邊完全一樣。

生（3號）我還有一種方法。我在樹葉的中間畫一條豎線，發現它正好是樹葉的對稱軸，所以我認為它是軸對稱圖形。

生（2號）我想補充一下：這里畫的不是一條直線，應該這樣畫。（示范畫點劃線）第三個圖形，誰來說？

生（3號）我覺得它不是軸對稱圖形。雖然外面的圓圈是對稱的，但里面的字母不是對稱的。

生（4號）因為它不能平均分成兩半。你看，假如從中間畫一條直線，它的兩邊是不對稱的。

生（2號）最后一個圖形，我來說吧。我覺得它是軸對稱圖形。把它從中間對折，它的兩邊應該會重合，所以它是軸對稱圖形。接下來，我們看一下第2題。誰來展示自己的作品？

生（4號）我的作品是一個京劇臉譜，它是軸對稱圖形。

生（2號）你是怎么剪出來的？

生（4號）我先把它對折，然后只要剪一邊，它的兩邊就都出來了。中間的折痕就是它的對稱軸。

生（3號）我剪的是一個杯子。我的方法和他差不多，也是先對折，然后只剪了一邊，就剪出來了。

生（1號）我剪了一個南瓜臉。我先把一張紙對折，然后畫了半個圓；剪完以后，再給它畫上眼睛和嘴巴。它是軸對稱圖形。

生（4號）我想補充一下：畫眼睛和嘴巴的時候，兩邊一定要一模一樣。

生（2號）最好是在對折后，先把一只眼睛和半張嘴畫好，這樣剪出來的圖形，才能保證是軸對稱圖形。

生（3號）我剪的是一個長方形，我覺得長方形就是軸對稱圖形。

生（1號）我有質疑。你在長方形的右邊寫了你的姓名，這樣兩邊就不對稱了。所以，長方形上最好不要寫姓名。

生（2號）如果要寫姓名，左邊和右邊要寫同樣的姓名，左邊的字還要反著寫。

生（3號）謝謝你的提醒。

生（2號）我剪的是一個胡蘿卜。我先拿一張彩紙，把它對折，然后用鉛筆畫出胡蘿卜的半邊，把它剪下來，就成了一個完整的胡蘿卜。大家同意嗎？

生（齊）同意！

生（2號）那么，我們來說第三題吧。第一個字母，誰來說？

生（1號）它是軸對稱圖形。因為它的上面和下面是完全一樣的，可以重合。

生（3號）我有質疑。它豎著看，左右兩邊沒法重合啊。

生（4號）我有個提醒：只要能分成一樣的兩半，它就是軸對稱圖形，不管它是左右分的，還是上下分的。

生（2號）我覺得有道理。那第二個字母，誰來說？

生（4號）第二個字母是軸對稱圖形。雖然它橫著、斜著對折都不能重合，但它豎著對折后兩邊完全重合，所以它是軸對稱圖形。

生（2號）我在第三個字母上畫了六條線，橫著、斜著、豎著都不能重合，所以它不是軸對稱圖形。

生（3號）我有補充：如果“S”上面的半圓和下面的一樣，那它就是軸對稱圖形了。

生（1號）我沒聽懂你的意思。

生（3號）我是說，如果這個字母變成“3”的樣子，那它就是軸對稱圖形了。

生（2號）有道理！第四個字母，誰來說？

生（3號）第四個字母是軸對稱圖形，雖然它上下對折不能重合，但是它左右對折能重合。

生（1號）最后一個字母不是軸對稱圖形。因為它不管左右對折，還是上下對折，哪怕斜著對折，都不能完全重合。

生（2號）大家說得非常好！我來總結一下。判斷一個字母是不是軸對稱圖形，不能只看一個方向，而要多試幾個方向。只要有一個方向上對折后能重合，它就是軸對稱圖形。最后，讓我們交流一下自己提出的問題吧。

生（1號）我提的問題是：學習軸對稱圖形有什么用？

（沒有同伴解答。）

生（2號）既然沒人解答，那我來說說我提的問題：漢字、字母、數字、圖形旋轉半圈，能重合嗎？

生（齊）什么意思？

生（2號）比如字母“C”，旋轉半圈后，能重合嗎？

生（1號）可以重合。只要是軸對稱圖形，不管旋轉到哪個方向，都可以重合。

生（2號）不對！你看字母“T”，旋轉半圈后，上面一橫轉到下面了，沒法重合了。

生（4號）但是，字母“S”是可以的——旋轉半圈后，它是能夠重合的。

生（2號）看來，有些字母、圖形旋轉半圈能重合，有些不能。下面討論誰提的問題？

生（3號）我帶來了兩個問題：軸對稱圖形在生活中有什么用？軸對稱圖形對生活有什么幫助？

生（2號）你這兩個問題是一樣的呀！一個意思。而且，和前面同學的問題也很像，沒法解答。

生（4號）我來說一下我的問題：軸對稱圖形可以有兩條對稱軸嗎？

生（3號）當然可以。

生（2號）不信的話，我現在給你畫一個。（畫出一個長方形）你看，這是一個軸對稱圖形吧。它橫著對折，豎著對折，都能夠重合，所以它有兩條對稱軸。

生（2號）現在看來，1號和3號同學的問題沒人能夠解答，我們小組就寫這個問題了。

（組長把1號和3號同學的問題寫在便簽條上，交給教師。）

在組內共學中，學生可以初步交流各自的思考，從而提升認識，形成共識。同時，也能初步交流各自獨立研究時遇到的問題。這時，部分問題可以得到解答，部分無法解答的問題則成為小組的公共問題，為下一階段組際之間的答疑互動提供了素材。

（三）組際答疑，在深度聯結中深化數學理解

師老師轉了一圈，發現我們班幾乎每一個小組都能在組長的帶領下進行有效交流，有對話、有追問、有回應、有總結。這才是小組交流應該有的模樣。當然，組內交流后，各個小組也在個體提問的基礎上，提出了代表小組的問題。我們一起來看一下。（匯總出示各個小組提出的問題，如圖4所示）快速瀏覽各個小組提出的問題，你能讀懂別的小組的問題嗎？

（學生快速瀏覽。）

師細心的同學一定已經發現，這些問題大概可以分為這樣幾類。先看第一列：如何判斷是否對稱？怎樣找對稱軸？三角形一定是軸對稱圖形嗎？對稱軸能斜著嗎？怎么剪軸對稱圖形？這是一組能夠幫助我們更好地理解軸對稱圖形的問題。再來看第二列：軸對稱圖形只有一條對稱軸嗎？正方形有幾條對稱軸？正六邊形是不是軸對稱圖形？圓有幾條對稱軸？這些問題都指向對稱軸的條數，尤其是我們熟悉的平面圖形究竟有幾條對稱軸。它們都是好問題！繼續看第三列，前兩個問題的視角已經從數學轉向現實生活了：生活中有軸對稱圖形嗎？學了軸對稱圖形有什么用？最后一個問題更有深度：除了軸對稱，還有別的對稱類別嗎？這個小組顯然不滿足于研究軸對稱了，還想向數學學習的更深處挺進。真好！接下來，我們就按從易到難的順序，集中全班的力量，一起來回應這些問題。好嗎？

生好！

師如何判斷一個圖形是不是軸對稱，或者是不是軸對稱圖形？怎樣找它的對稱軸？對這一組問題，是直接回應，還是先在小組里二度討論？

生直接開始。

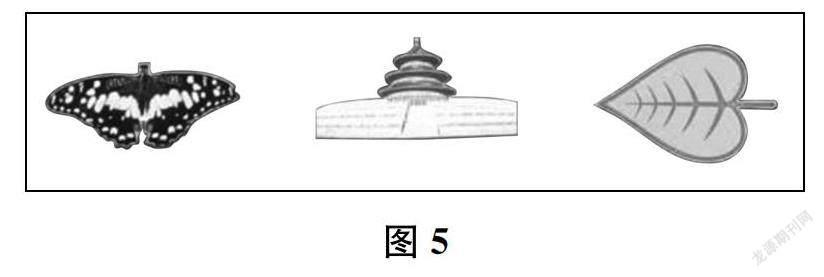
師（板貼，如圖5所示）黑板上，老師正好貼了三個生活中的圖案。它們是軸對稱圖形嗎？誰能代表你們小組，和大家分享你們的觀點？

生我覺得這里的蝴蝶、天壇、樹葉都是軸對稱圖形。

師臺下的同學如果同意，請一起拿手比畫一下，它們的對稱軸究竟在哪里？

（學生比畫。）

師奇怪，這里的對稱軸，有些是豎著的，有些是橫著的，那會不會出現斜著的？

生會。（把樹葉圖旋轉45度）這時，樹葉的對稱軸就是斜著的。

師看來，軸對稱圖形的對稱軸的方向不只有橫著或豎著的，也可以是——

生斜著的。

生我有補充。軸對稱圖形的方向發生變化，對稱軸的方向也會跟著變化。

師聊著聊著，第8小組的問題也被我們順便解決了。那你們是怎么判斷一個圖形是不是軸對稱圖形的？

生可以用眼睛看。如果一個圖形的左右或上下兩部分是完全一樣的，那它就是軸對稱圖形。

師觀察，的確是判斷的一種好方法。

生我覺得看有時不準，我們可以用對折的方法來判斷。比如，我們把天壇圖從中間對折一下，它的左右兩邊重疊在了一起，所以它是軸對稱圖形。

師是部分重合還是完全重合？

生完全重合。

師看來，對折是一種更專業的方法。討論到現在，第1小組的前半個問題已經有答案了，那后半個問題呢？

生我覺得對稱軸就在對折的地方。

師數學上，折痕所在的這條直直的線，就叫對稱軸。（示范畫對稱軸）現在，第1小組的問題討論完畢。而第2小組顯然并不滿足于如何判斷一個圖形是不是軸對稱圖形，他們想知道究竟應該如何剪出一個軸對稱圖形。誰有好辦法？

生其實，學習單已經告訴我們怎樣剪出一個軸對稱圖形了。

師打斷你一下：如果讓你用三個字來概括一下剪軸對稱圖形的方法，你會選擇哪三個字？

生（略作思考）我覺得應該是折、畫和剪。也就是先把長方形紙對折，再畫出軸對稱圖形的一半，最后沿著畫好的線把圖形剪下來，就可以得到一個軸對稱圖形。

師老師這兒就有一張白紙，你愿意向大家現場演示一下如何用“三字口訣”得到一個軸對稱圖形嗎？

（學生上臺演示。教師相機完成板書，如圖6所示。）

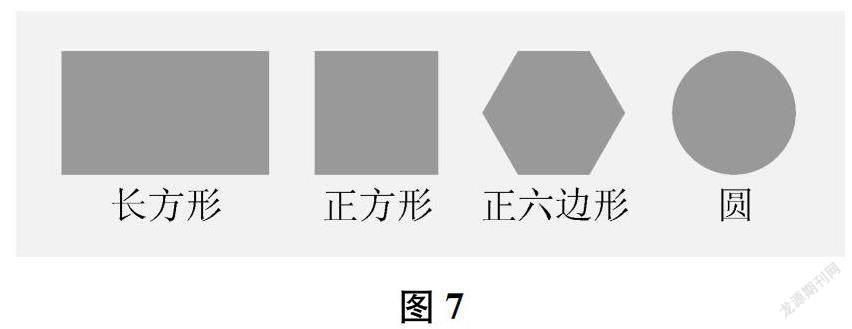
師解決完前兩個相對比較基礎的問題后，來看大家特別感興趣的第二列提問：對稱軸只有一條嗎？長方形、正方形、圓等是不是軸對稱圖形？又有多少條對稱軸？（出示圖7）老師提前準備了這幾個圖形，誰能結合這些圖形，具體回應一下這幾個問題？

生我覺得，有些軸對稱圖形只有一條對稱軸，比如之前的三個圖形。但有些圖形有兩條對稱軸，比如長方形。

生我反對！（上臺同步比畫）我覺得長方形有四條對稱軸。師出現兩種不同的觀點了。怎么辦？

生大家看，我們的學習單就是一個長方形。我覺得，（橫著對折后指著折痕）這是它的一條對稱軸，（豎著對折后指著折痕）這也是它的一條對稱軸，所以它有兩條對稱軸。

你漏了兩條對稱軸：長方形中，還有兩條斜著的對稱軸。

生我覺得斜著的兩條不是對稱軸。

師長方形到底有幾條對稱軸？誰能從板書中找到判斷的依據和方法？

生我們可以把長方形折一折。大家看，（同步演示）如果把長方形橫著對折或豎著對折，兩邊都可以完全重合；但是，如果把長方形斜著對折，兩邊不能完全重合。

師看來，判斷一個圖形是不是軸對稱圖形，或者判斷它有幾條對稱軸，光靠看還不行，有時還得動手折一折、比一比。現在，你能確定長方形有幾條對稱軸了嗎？

生兩條。

師那正方形、正六邊形和圓又有幾條對稱軸呢？如果大家的觀點不一致，我們將再次通過折一折、比一比來判斷。

生我覺得正方形有四條對稱軸，它們就像一個“米”字一樣。

生我覺得正六邊形有三條對稱軸，一條豎著的，兩條斜著的。

生不對，正六邊形應該有六條對稱軸。

（該生上臺比畫，臺下同學掌聲通過。）

生我覺得圓有無數條對稱軸。

生無論從哪個方向對折，圓的兩邊都能完全重合，所以圓有無數條對稱軸。

師判斷這些平面圖形是不是軸對稱圖形、有多少條對稱軸，應該是小學高年級才探討的話題。然而，正是因為大家的主動提問，我們才有機會在二年級時就對這些話題有了初步的思考。當然，到了高年級，我們會繼續就這些話題展開更深入、更專業的研究。接下來，敢不敢研究更有挑戰性的問題？

生敢！

師除了軸對稱之外，還有沒有別的類型的對稱？

生有！中心對稱。

師（板書：中心對稱）能不能告訴大家，你是從哪兒知道中心對稱的？

生我在課前查閱了資料。比如，圓就是中心對稱圖形。

生我也查閱了資料，把一個圖形旋轉半圈后，如果和原來的圖形完全重合，它就是中心對稱圖形。

師大家是有備而來啊！那么，學習單上的五個字母中，有沒有中心對稱圖形？

生我覺得字母“S”就是中心對稱圖形。

生我想向大家演示一下。（上臺同步演示）把字母“S”繞著中間這一點旋轉半圈，正好和原來的字母完全重合，所以它的確是中心對稱圖形。

師除了“S”以外，26個字母中還有中心對稱圖形嗎？黑板上的四個平面圖形中，哪些也是中心對稱圖形？帶著這些新問題，讓我們課后繼續展開研究。最后，讓我們聚焦今天這節課的最后一個問題：生活中，你見到過軸對稱圖形嗎？

（學生小組討論后匯報——）

生我們佩戴的紅領巾，就是軸對稱圖形。

生教室的窗戶由兩個相同的部分組成，它也能看作軸對稱圖形。

師當我們帶上數學的眼光觀察現實世界時，生活中隨處都能看到軸對稱圖形的影子。老師課前也找來了一些生活中的畫面，你能從中看到軸對稱圖形嗎？如果能，用手比畫一下它的對稱軸。

（教師出示圖片，學生一一判斷并比畫。）

師課的最后，老師也為大家留下一個問題：為什么生活中大量的建筑、剪紙、京劇臉譜等都設計成軸對稱圖形？這背后的原因到底是什么？讓我們帶著問題走進課堂，再帶著新的問題離開課堂。

在組際交流中，由于每一個問題都是小組成員共同推薦的，加上教師精準的介入、引導與點撥，學生原有的模糊理解、膚淺表達、零散認知等不斷得到澄清、深化與結構化。更有深度的學習正是在這樣的組際互動與教師引導中得以發生。

二、教學反思

回顧完整的課堂學習歷程，不難發現：“學生提問”的確是撬動學生深度學習的有效抓手。

首先，經由充分的訓練與實踐，學生完全具備提出問題、提出高質量問題的能力。他們所提的問題并不局限于依托數量關系所構想的常規數學問題，而能將觸角伸向數學學習的關鍵處，指向思維的不足處。課例中，學習單呈現的軸對稱圖形的對稱軸基本都是橫平豎直的，學生由此提出“對稱軸可以斜著嗎”；當學生發現長方形、正方形永遠都是軸對稱圖形后，便提出了“三角形一定是軸對稱圖形嗎”；當整個學習單都要求研究軸對稱圖形時，學生提出“除了軸對稱，還有別的對稱類別嗎”……這樣的提問，不落俗套，真正反映了學生思維的盲區，指向數學學科的本質。

其次，學生自主提出的問題數量眾多、難以預設，在討論過程中還會生成新的問題，這給教師的課堂調控帶來了巨大的不確定性和挑戰。對此，一方面，教師需要提前了解學生自主提出的問題，做到心中有數、未雨綢繆；另一方面，面對學生小組共學后涌現的團隊提問，教師要能快速進行甄別、分類、排序、整合，并且就若干核心問題如何引導學生展開討論、如何促發學生深度思考，作出提前預判和有效規劃。課例中，各小組看似提出了10個不同的問題，然而，只要對這些問題稍加梳理與歸類，便不難發現，它們主要涉及“如何判定和創作軸對稱圖形”“如何判定對稱軸的條數”和“軸對稱圖形在生活中有怎樣的應用”這三個維度。由此，教師得以從紛繁復雜的問題碎片中抽身出來，而將所有精力聚焦到這三個被各個小組普遍關注的核心、關鍵問題上，并由此引導學生展開新的討論。當然，這對教師的臨場應變能力提出了更高的要求，也對教師的備課能力提出了新的期待，包括對數學知識的本質要有準確理解，對課程內容的重難點要有深刻洞見，對學生學習的經驗起點、思維路徑和方式要有精準把握，對如何基于“學生提問”把他們的思維與認識由模糊引向清晰、由膚淺引向深刻、由單一引向多元、由零散引向結構等要有清晰的規劃。

最后，教材與教參預設的問題往往基于“教的邏輯”，基本規定了課堂可觸及的邊界。而由“學生提問”引領的數學課堂更側重于“學的邏輯”，關注學生的真實困惑和學習體驗，關注學生的好奇心和求知欲。學生的提問會面向所有的未知世界展開，這決定了課堂的原有邊界會被打破，課堂將向四面八方打開。這樣的課堂固然會因為充滿未知和不確定性而讓教師深感不安，但同樣會因為開放性和生成性而展現出獨特的吸引力。在這樣的課堂中，只要是有價值的問題、能引發學生深度思考的問題，都可能成為大家共同討論的焦點。課例中，原本并不屬于這堂課的“三角形一定是軸對稱圖形嗎？”“長方形、正方形、圓等是不是軸對稱圖形？各有多少條對稱軸？”“除了軸對稱以外，還有別的對稱類別嗎？”等問題便紛至沓來，進而，因為未知和不確定性而帶來的探究樂趣、思維樂趣便一點點被點燃。正是在這樣的教學邏輯中，“學生提問”真正讓學習成為一場知識的歷險，成為一次面向未知的深度探秘，高品質的深度學習便有可能真正發生。

參考文獻：

［1］ 郭華.深度學習及其意義［J］.課程·教材·教法，2016（11）：2532.