小學數學跨學科主題學習的內涵、意義及實踐路徑

【摘 要】跨學科主題學習是以培養學生綜合運用所學知識和方法解決實際問題為目標展開的學習方式，具有學科性、境脈性、協作性和融合性等特征。在數學教學中，教師可以通過確立真實性主題、梳理結構化內容、解構遞進式任務，圍繞大概念的理解展開整合性評價，逐步培養學生的核心素養。

【關鍵詞】小學數學；跨學科主題學習；真實性主題；結構化內容；遞進式任務；整合性評價

【中圖分類號】G623.5? 【文獻標志碼】A? 【文章編號】1005-6009（2023）09-0040-06

【作者簡介】莊治新，江蘇省無錫市新吳區坊前實驗小學（江蘇無錫，214111）副校長，高級教師，無錫市數學學科帶頭人。

跨學科主題學習活動強調課程的綜合實施，重在加強學科間的聯系，強化實踐性要求?！读x務教育數學課程標準（2022年版）》強調“綜合與實踐”是小學數學學習的重要領域，包括主題活動和項目學習。作為“綜合與實踐”的主要展開形式之一，數學跨學科主題學習成為培養學生核心素養，促進他們形成正確的價值觀、必備品格和關鍵能力的必要學習方式。

一、數學跨學科主題學習的內涵

1.數學跨學科主題學習的概念

美國學者克萊恩和紐威爾強調，跨學科研究是一項回答、解決或提出某個問題的過程，旨在整合兩個或多個不同的學科，重點關注跨學科活動或跨學科理解的結果。我國西南大學趙伶俐教授等學者指出，要把學科之間出現的問題當作跨學科研究的對象，強調學科間的有機融合。跨學科學習既是一種以跨學科意識為核心的課程觀，也是一種融綜合性與探究性為一體的深度學習方式，還是一種以綜合主題為基本呈現方式的特殊課程形態。

跨學科主題學習是基于學生的知識基礎，圍繞某一研究主題，以某一學科課程內容為主干，運用并整合其他課程的相關知識和方法，開展綜合學習活動的過程。數學跨學科主題學習是指跨學科背景下的數學內容學習，其目標是引導學生在跨學科的背景下用數學的眼光觀察現實世界，用數學的語言表達現實世界中事物的概念、關系和規律，感悟數學與現實世界的聯系，培養實踐精神。

由此可見，小學數學跨學科主題學習應以大概念為核心，以小學數學學科為主陣地，結合真實情境中具有挑戰性的問題，打破學科界限，從跨學科的視角設計有價值的主題學習任務，實現學習內容的綜合化。通過將數學與其他學科有機融合，促使學生在不同的學習內容之間建立有意義的聯結，跳出單學科研究的視野局限，用跨界的眼光觀察生活，用大概念解釋生活現象，靈活運用習得的知識解決生活中的問題，在不斷深入的學習活動中產生跨學科基礎的創新與創造。

2.數學跨學科主題學習的特征

學者曼西利亞強調跨學科研究的三個特性：一是意圖性，拓展對某個問題的認識；二是學科性，要基于學科知識及其思維模式特點；三是整合性，重在整合而不是并列各種學科視角。數學跨學科主題學習強調真實情境中的數學/跨學科概念整合，它主要具備以下特征。

一是學科性。真正的跨學科主題學習要解決的是學科本身的任務，是對學科知識的應用。數學跨學科主題學習要圍繞數學概念展開，學生要主動用數學的思維方式去分析、思考、解決真實問題或其他學科的問題，從而更深刻地認識學科的本質。如在跨學科主題學習活動“校園路線設計”中，大概念是“數據可以使圖形更精準”，數學核心概念是“比”“比例”，雖然有語文、美術等學科的內容，但最主要的還是數學學科本身的價值?？鐚W科主題學習要堅持學科立場，只有學好學科知識，才能跨學科地解決問題，或者在學科內借助其他學科的工具來解決問題。

二是境脈性。任何知識的發生、發展都有特定的情境脈絡，情境任務必然蘊含著問題與活動，也必然存在著不確定性和挑戰性。數學跨學科主題學習是用數學大概念去解決連續的、動態的場域組合中的真實問題，強調有序互動及有效對話。如“校園路線設計”就是基于真實問題場域，學生要參與校園路線的設計，數據的采集、平面圖的設計等對他們而言都具有極大的挑戰性，正是這些持續性的真實問題，促使學生全身心地投入“比”“比例”“比例尺”等數學概念的學習，并利用它們創造性地解決問題。

三是協作性。復雜的挑戰性任務一定需要團隊協作，每個人都要在參照、考慮同伴的過程中使自己的行動更有意義和方向。數學跨學科主題學習就是圍繞數學大概念展開的同伴協作活動。如在“校園路線設計”中，學生需要分組完成測量并在班里進行分享：借助身體尺一步或一庹來估測距離、使用指南針或量角器來確定方位、利用米尺或卷尺來測量長度等；還需要團隊協作完成方案：在質疑中引發對平面圖精確性的思辨、在商議中形成對比例尺合理性的理解、在討論中梳理對路線可行性的認同等。數學跨學科主題學習讓學生在理解數學概念的過程中感受個人力量，更在主動解決真實問題的過程中深切體會與他人共同成長的必要性。

四是融合性。數學的交叉與整合是由數學的本質決定的，是數學發展的時代特點。數學跨學科主題學習雖然以數學學科為核心，但任何一個真實情境中的活動必定是跨學科的。如在“校園路線設計”中，主要圍繞數學大概念“數據可以使圖形更精準”展開探究，而在繪制平面圖時又需要使用美術學科中“構圖”的概念使平面圖更具結構性，在設計路線時還需要使用語文學科“移步換景”的概念使景點介紹更有條理性，三門學科有機融合能使跨學科主題學習更具社會價值和生活意義。

二、數學跨學科主題學習的意義

1.打通現實生活與數學學科的壁壘

數學概念具有明顯的學科特征，而一個完整的人的生活是不分科的，這就使得數學學習與學生生活之間產生了隔閡。數學跨學科主題學習可以使抽象的、嚴謹的數學概念與有趣的、鮮活的生活經驗緊密結合。如教學“比例尺”，可以設計跨學科主題活動“校園平面設計”，讓學生測量校園的長和寬，并根據圖紙大小找到合適的比例尺，從而使他們在選擇方法、調整數據的過程中將比例尺與實際生活相結合。通過數學跨學科主題學習，將數學概念融入學生的現實生活，在有意義的實踐活動中將生活經驗提升到學科的高度，能在一定程度上實現人的完整生活與數學學科的意義聯結。

2.強調在真實情境中的素養提升

《中國學生發展核心素養》中所提出的素養是融合性目標，必須在融合性學習中才能實現。引導學生運用學科觀念與跨學科觀念解決真實問題，不斷發展學科理解力與生活理解力，并在此過程中掌握知識與技能，是跨學科主題學習的本質。在教學中，如果教師只把書本上的內容教給學生，那學生就僅僅是知道那些內容、見到了知識的影子而已，只有將其置于真實情境中，學生才能真正了解它的全貌并能靈活地運用。如教學“比例尺”，在跨學科主題學習中，學生在解決真實情境中“如何確定合適的比例尺”這一關鍵問題時，需要利用數學/跨學科知識進行校園大小的測量與估計、數據的調查與分析、方案的選擇與調整等，這個過程既是用數學的眼光觀察現實世界、用數學的思維思考現實世界、用數學的語言表達現實世界的過程，也是注重與他人交往、合作、共同進步的過程，是學生核心素養形成的過程。

3.實現社會價值與數學學習的深度融合

北京師范大學劉堅教授認為：指向核心素養的教育更加強調課程內容與變化的世界的聯系，更加強調任務驅動學習和跨學科主題學習。學校的學科教學要具有更開闊的視野，要引導學生通過學科和跨學科學習來理解世界。培養學生，就是為了他將來進入社會能夠從事創新性實踐。如“校園路線設計”就是要讓學生像一名真正的建筑繪圖師那樣，會將立體建筑解構并轉化成相應的平面圖，在實踐探究和概念習得的雙線推進中形成對平面圖形的個性化理解，而個體與團隊協作中的不確定性、測量方法的不一致性、平面草圖繪制的差異性等，會讓學生體驗到要在不確定性中追求確定性。數學跨學科主題學習不僅要讓學生知道數學概念是什么，更要讓他們能用行動來證明，這就是有價值的概念習得，更是一種雛形的社會生活樣態。

三、數學跨學科主題學習的實踐路徑

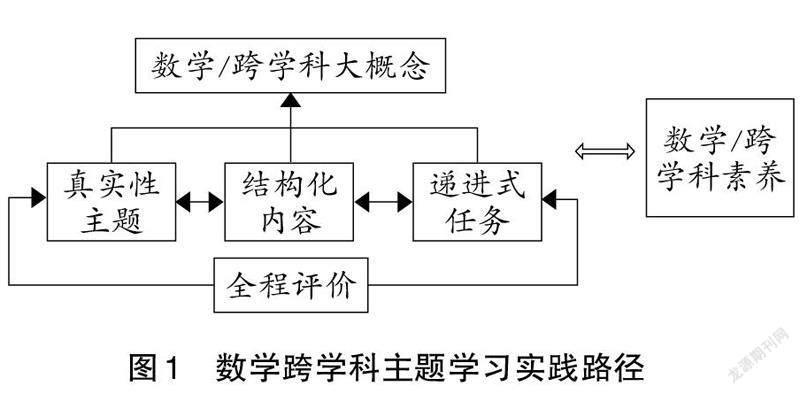
數學跨學科主題學習以解決真實情境中的問題為重點，旨在強化學生對數學本質的理解，重在培養學生的實踐精神、應用意識和創新意識。在教學中，教師要注意以數學/跨學科大概念為軸心，合理整合教學內容，形成“主題—內容—任務”的實踐路徑，通過全程評價引發學生對數學/跨學科概念的深度理解，（如圖1）促進他們數學素養和跨學科素養的提升。

1.確立真實性主題：數學學科與現實生活進行聯結

一個真正的跨學科研究主題，無論是跨越學科還是來自學科，都必定具有復雜性和綜合性。這意味著該主題是一個內涵豐富的問題域，而不是一個單向度的知識命題。數學跨學科主題需要結合真實情境來確定，這里的真實情境可以包括：（1）學校發生的事件，如學校食堂每天都會有些糧食被浪費，請你了解原因并發出倡議（節約糧食）；（2）社會生活中的事件，如很多小區車輛不斷增加導致車位緊張，請你全面分析并合理設計方案（車位布局）；（3）現實世界中的事件，如央行調整了存款利率，請你為不同人群定制個性化的存款方案（利率問題）；（4）與傳統文化相關的情境，如古人有在中秋節放孔明燈的習俗，以寄托對家人的思念和祝福，請你了解相關文化并親手設計、制作一盞孔明燈（孔明燈的故事）；（5）數學史料中的情境，如三角形有無數種形狀，而每副三角尺都只有兩種形狀，請你從數學家的視角分析原因（三角尺的秘密）。

無論哪一類主題，都要以數學概念的理解為核心，從數學知識、數學方法、數學思維等維度深入剖析數學內涵，實現數學學科與現實生活的聯結。如在“校園路線設計”中，學生要為幼兒園大班的小朋友提供精準的校園平面圖，規劃出合適的路線并進行介紹，這是學生主動將“比”“比例”“確定位置”等數學概念與校園生活相融合的過程，在圍繞主題推進測量校園、繪制平面圖、規劃路線等任務的過程中，賦予數學概念以生活的意義和價值。一個真實性主題的確立，既要考慮數學學科的內涵，也要鏈接現實生活；既要具有挑戰性，也要具有趣味性。

2.梳理結構化內容：數學概念與跨學科概念有機整合

心理學家皮亞杰指出：一切社會的研究都必然要導向結構主義。數學跨學科主題學習解決的是真實情境中的問題，需要教師引導學生圍繞數學概念主動進行有意義的認知結構重組，其作為綜合性的研究，更需要跨學科概念的支撐。這里的重組主要包括：（1）相似學習內容的整合，如長方體、正方體、圓柱、圓錐的認識（數學）與立體紙柱造型（美術）研究的都是立體圖形，有利于學生全面了解立體圖形的結構特征；（2）具有內在關聯的內容整合，如幾和第幾的認識（數學）與隊列隊形（體育），一年級學生在排隊報數游戲中可以形成對基數與序數的整體性理解；（3）問題解決需要的內容整合，如在面對“學校籃球隊隊員選拔”這一問題時，需要解讀籃球賽制（體育）、統計與分析隊員身高及耐力等數據（數學）、整合數據并生成雷達圖（信息技術），這三者的有機整合有助于學生直觀、全面地分析和解決問題；（4）與主題相關的內容整合，如主題“穿梭時光”，將認識鐘表、24時記時法、年月日等數學知識與相冊制作相關的信息技術有機整合，有助于學生建構對“時光”的整體認知和情感體驗。

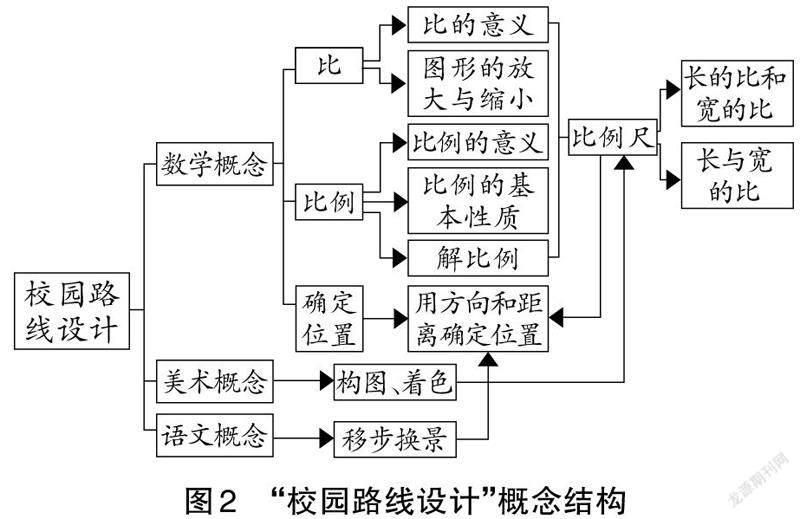
只有將有聯系的數學概念與跨學科概念有機聯結，使零散的、碎片化的知識聚合起來，使學生形成對數學/跨學科概念的結構化認知，他們才能深度理解數學/跨學科概念?！靶@路線設計”的概念結構如下頁圖2所示，主要運用“比”“比例”“比例尺”“確定位置”等數學概念解決繪制校園平面圖的問題，同時又需要將它們與科學測量、美術構圖、語文寫景等多個學科概念有機整合，從而使校園平面圖的設計與繪制更加科學精準，更具美感與文化內涵。將數學概念與跨學科概念有機整合，打通了數學與其他學科的邊界，概念與概念之間相互影響、彼此交融，形成有意義的知識結構，有助于促進學生學會用整體的、聯系的、發展的眼光看問題，養成科學的思維習慣。

3.解構遞進式任務：概念理解與實踐循證齊頭并進

數學跨學科主題可由遞進式的任務鏈組成，每一個任務鏈又由多個學習實踐活動并聯或串聯而成。不同的學習實踐承載著不同的育人功能：（1）知識習得類實踐，重在對基本知識和技能的掌握，如自學或互學有關平面圖形的面積計算方法；（2）討論交流類實踐，重在問題的多樣化表達和解決，如小組商議合適的出行方案；（3）調查統計類實踐，重在獲得真實而相對全面的資料，如到每個班級去統計學生喜愛的校服款式；（4）探究實驗類實踐，重在對比研究中獲得有價值的發現，如探究發現食物在烹飪過程中重量的變化規律；（5）操作測量類實踐，重在借用工具獲得必要的數據，如測量校園綠地面積；（6）場館尋訪類實踐，重在沉浸式地體驗場館文化，如去博物館了解吳文化的歷史。無論是哪一類學習實踐活動，都要圍繞任務目標展開，既重視學科基本知識和技能的掌握，又關注跨學科素養的培育。

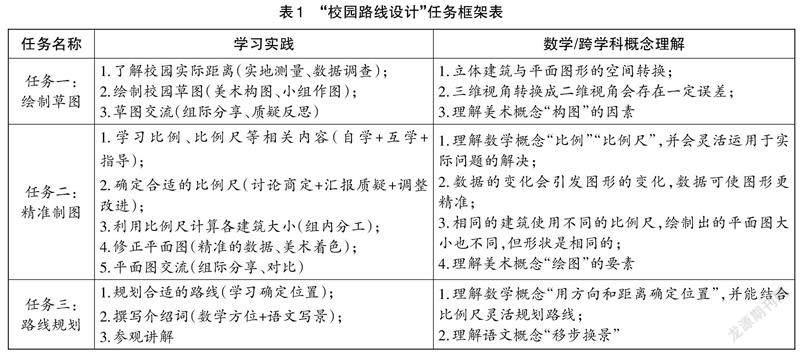
任務鏈中的各項任務既相互聯系又各有側重，學生參與學習實踐的過程就是不斷剖析、理解大概念的過程。真實情境中的活動任務不僅能引發學生對問題解決的深入思考，更能促進他們在實踐循證中逐步形成對數學概念的深度理解?！靶@路線設計”中分解出的三個遞進式任務鏈如表1所示，學生經歷了多個學習實踐活動，逐步體會到要像一名真正的建筑繪圖師那樣思考問題：如何將立體建筑繪制到平面圖紙上？如何理解每個建筑與平面圖形之間的關聯？如何精準而科學地繪制平面圖？……圍繞主題的任務分解，使問題解決的路徑更清晰，學生在主動參與實踐循證的過程中對數學/跨學科概念形成了深度理解。

4.注重整合性評價：數學素養與跨學科素養相互融通

整合性評價強調在真實問題情境中考量學生的素養表現。數學跨學科主題學習需要遵循整合性的評價邏輯，表現為評價類型和方法的多元化，包括對概念理解的表現性評價、對探究實踐中的過程性評價、對問題解決的終結性評價等，也包括在活動推進過程中的自評與互評、在同伴協作過程中的提醒與調節、在問題解決過程中的主動性與參與度等；可以是基于量規的量性評價，也可以是基于證據的質性評價。如“校園路線設計”中圍繞“平面圖繪制交流”，從概念理解、運算能力、數學表達、團隊合作及學習狀態等五個維度設置了評價量規（如表2），既指向學生對數學概念的深度理解，又指向他們協作、自律等綜合素養的形成。數學跨學科主題學習既關注學生數感、空間觀念等數學素養的培育，更指向會協作、有擔當、懂謙讓等綜合素養的形成。

綜上，數學跨學科主題學習既有助于學生體會數學與其他學科以及社會生活之間的聯系，又能使他們在持續的學習實踐中積累活動經驗，感悟思想方法，提高解決實際問題的能力，形成和發展核心素養。

【參考文獻】

［1］唐磊.理解跨學科研究：從概念到進路［J］.國外社會科學，2011（3）：89-98.

［2］張華.跨學科學習：真義辨析與實踐路徑［J］.中小學管理，2017（11）：21-24.

［3］孟璨.跨學科主題學習的何為與可為［J］.基礎教育課程，2022（11）：4-9.

［4］安東尼·杰克遜.全球勝任力——融入世界的技能［M］.吳敏，譯.上海：華東師范大學出版社，2020.

［5］黃翔，童莉，史寧中.談數學課程與教學中的跨學科思維［J］.課程·教材·教法，2021，41（7）：106-111.

［6］崔允漷.如何開展指向學科核心素養的大單元設計［J］.北京教育：普教版，2019（2）：11-15.

［7］徐玲玲，劉徽，曹琦.評價連續體：大概念教學的評價設計［J］.上海教育科研，2022（1）：19-24.