大單元視角下的數學建模和數學探究
施維
【摘要】大單元視角下,教師應如何貫徹落實對現實問題進行數學抽象,進而建立數學模型,以及如何落實探究式教學,本文借助教材中的三角函數與楊輝三角進行一些研究.
【關鍵詞】高中數學;大單元教學;數學建模
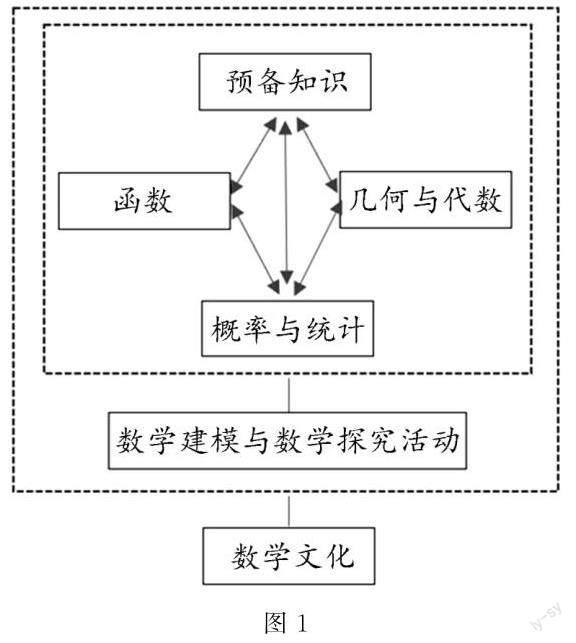
《普通高中數學課程標準》(2017年版)(以下簡稱《新標準》)中把函數、幾何與代數、概率與統計、數學建模與數學探究活動作為高中數學知識的四條主線內容,這四條主線與初中數學中的四條主線相一致,知識難度呈螺旋狀上升,增加了預備知識.這四條主線與預備知識和數學文化間的基本關系如圖1.
《新標準》中提出六大數學學科核心素養,數學建模這一核心素養是指通過對現實生活中的實際問題進行數學抽象,讓學生用數學語言表征問題、用數學方法構建模型從而解決問題的素養.數學探究活動是指圍繞某個具體的數學問題開展自主探究、合作研究并最終解決數學問題的過程.數學探究與數學建模可以很好地培養學生的創新意識與實踐能力,同時學以致用,體會數學來源于生活又可以運用于生活中,從而使數學與生活不再脫節.
1 大單元的框架結構下進行的數學探究活動和數學建模
新教材在設計時,知識符合學生的認知規律,采用螺旋上升的方式編排,在各個主線的研究過程中很注意整體性,以及前后知識之間的上下位關系.例如,在函數主線中,要解決函數的概念、函數的性質、基本函數類、函數的應用、思想和方法.例如,在前面幾節介紹完函數的概念、性質以后給出冪函數的圖象與性質,通過前面一直貫穿的數形結合思想來研究冪函數的性質,為后來學習其他幾種函數提供了方法支持.冪函數、指數函數、對數函數都存在增函數的情況.
例如 以一次函數y=kx(k>0)、指數函數y=ax(a>1)、對數函數y=logax(a>1)為例來研究三種函數的差異,而這種差異正是不同類型現實問題具有不同增長規律的反映.接下來分析三種不同函數的增長方式,以便用不同的函數模型刻畫現實生活中的變化規律.刻畫循環往復、周而復始規律的最典型的函數模型就是三角函數.而具有周而復始變化規律最典型、最熟悉的模型就是勻速圓周運動,接下來在整個三角函數一章始終貫穿用單位圓來研究三角函數,借助圓來研究三角函數就是這一章節的主線,通過這些可以看出教材的設計很注重整體性和連貫性.
在三角函數部分,開頭就用圓周運動引入,整個章節通過單位圓定義三角函數的概念,也是通過單位圓來研究三角函數的性質以及兩角差與和的正弦余弦公式等,以便于學生理解三角函數是用來刻畫周而復始現象的.再來回歸現實解決問題,通過對筒車模型的研究,一是把數學與中國古代人們的智慧結晶相結合;二是便于學生理解y=rsinωx+φ+h中各個字母的含義,為接下來進行的數學探究A,ω,φ對y=Asin(ωx+φ)圖象的影響奠定認知基礎.最后研究了生活中常見的一些三角函數可以刻畫的模型,如彈簧振子、交變電流、潮汐現象等.又把數學與生活聯系起來,整個章節的構想具有整體性,且具有生活氣息,使數學活了起來.
2 數學建模和探究式教學所遵循的原則
2.1 自主探究與小組合作相結合的原則
數學探究和數學建模的意義在于培養學生成為全面可持續發展的人,教學過程中要充分體現學生是學習的主人,必須先自主探究和獨立思考,再進行小組討論,經過小組整合以后,整理提出的問題,進而尋求解決問題的辦法.
2.2 以問題為主線的原則
探究式教學是以學生自主思考、合作探究為主的教學模式,數學建模也是由學生為主體的活動,必須貫徹教師是課堂的引導者,以問題引導的方式保證學生課堂主體的地位.好的問題是高效課堂的保障,學生想在有限的課堂教學時間內完成高質量的數學建模和數學探究活動,教師一定要進行充分的備課,了解學情,設計一系列引導性的問題串,在學生理解困難處和疑惑處搭建腳手架,使學生可以“跳一跳,摘個桃”,也就是問題的設計要符合學生的最近發展區.同時,課堂中教師要隨時注意學生提出的問題,學生想到的問題可能不是正確的,但這就是學習的過程,符合桑代克提出的試誤——聯結學習理論,犯錯證實學習在真實地發生.學生提出問題(哪怕是錯的)比解決問題來得更為重要,能發現問題才是教育的最終目的.
例如 在高中數學人教A版選擇性必修三第六章最后一節“數學探究:楊輝三角的性質與應用”中可以設計如下問題串.
問題1 對比二項式系數表與楊輝三角,你有什么發現?
追問1 請同學們觀察這兩個數表,你能把二項式系數表與楊輝三角統一起來嗎?
結合教材中的兩個圖,可以發現楊輝三角比二項展開式多了一行,把第一行記為第0行,則楊輝三角的第n行的第r個數可以表示為Cr-1n,第n行就是(a+b)n的展開式的二項式系數.
問題2 先從整體觀察楊輝三角中數字的結構,即楊輝三角這一數字三角形中數字排列的規律.
追問1 再細致地觀察每一行、相鄰兩行、斜行等的規律.
追問2 通過畫一畫、連一連、算一算這樣的數學實驗,驗算一下你發現的規律.
追問3 寫出你發現的結論,這些結論能否用組合數表示?
通過問題串的形式,引導學生逐步地學會數學探究的方法,先是表征問題,然后就是帶著問題,觀察、思考、分析,提出有意義的數學問題,猜測、歸納和猜想,再到推理和論證,這就是一個完整的數學探究過程.帶著問題使課堂更高效,這節課教學的重點是教會學生數表的探究方法.通過本節課,學生知道數學探究要觀察,可以先整體再局部,先猜想再論證,先類比模仿再創新實踐.
2.3 以信息技術輔助教學
人類已經進入大數據時代,數學的研究領域和應用范圍得到的拓展,數學直接為社會創造價值,推動社會生產力的發展.同時信息技術的發展也能反哺數學的研究與教學,讓數學建模和數學探究活動變得生動和有趣.直接的優勢就是:計算機將數學建模問題和數學探究的求解變得異常直觀、清晰、透徹.這也符合大數據時代數學的經濟價值和應用價值,同時信息技術反作用于數學研究.
例如 高中數學人教A版必修第一冊5.6.1勻速圓周運動的數學模型,通過筒車模型進行的數學建模活動,可以通過GGB軟件把模型簡化.
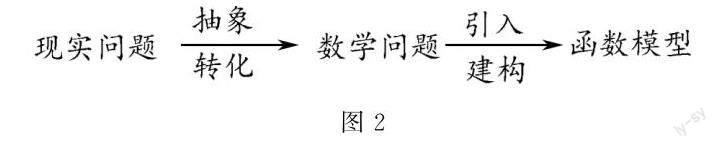
通過對幾何圖形的研究很容易把實際問題抽象轉化為數學問題,進而解決數學問題,進一步引入、建構函數模型問題,經歷的過程如圖2.
同樣地,在數學探究過程中,由于數學太抽象,配以動態的信息技術手段能使問題變得生動,學生不光可以聽見還可以看見,甚至動手操作,這樣數學探究的難度就會降低,如在5.6.2函數y=Asin(ωx+φ)中可以通過幾何畫板或者GGB軟件來演示三個參數A,ω,φ對函數y=Asin(ωx+φ)的影響.
2.4 充分考慮學生的學情
《新標準》指出,數學教學也是教育的重要部分,其根本任務也是立德樹人,最終要實現人人都能獲得良好的數學教育,不同的人在數學上得到不同程度的發展的目的.而數學探究活動和數學建模活動就是實現這一目標的有效抓手,數學探究活動和數學建模都是以自主探究和小組合作來進行的.
例如 在高中人教A版數學選擇性必修三中,對楊輝三角的性質與應用一節的數學探究,先進行自主思考,對數表的探究是個比較簡單的任務,就是學生很喜歡的找規律,使每個學生都能思有所得,從而實現每個人都能學有所得.再進行小組交流,在思辨討論中知識產生了,語言表達能力提高了,思維得以碰撞,眼界得以開闊.在分組時充分考慮學情,采用組間同質、組內異質的原則分組.小組交流時每個同學提出自己的意見,經過小組分析、辯論以后產生的才是知識.小組在激烈討論時,以及全班同學共同研討時,實際上就是在進行頭腦風暴,就是創造性思維訓練,最后就能實現對創新意識的培養.
3 數學探究活動、數學建模與數學文化一脈相承
楊輝三角是我國古代數學的偉大成就,教科書因為楊輝三角在數學和數學思維上的價值(人們研究數表由一行到多行,一兩條性質到一系列性質,從個別到系統,都體現數學知識的獲得過程,即由淺入深,由特殊到一般,通過楊輝三角的研究先整體再到局部,由觀察到歸納到猜想論證,體現了完整的數學探究的過程),又具有審美價值和具有多元化的特性(中國、歐洲、阿拉伯等地的眾多數學家都曾研究和應用它),對于培養學生的數學思維、開闊眼界有重要價值,從而設置了數學探究欄目,使學生通過數學探究活動提高認識的同時,全面提高學生數學學科核心素養,以此培養學生的民族自豪感和一探究竟的興趣.
例如 在高中數學人教A版必修第一冊“5.6.1勻速圓周運動的數學模型”一節中,筒車是我國古代發明的一種水利灌溉工具,經濟又環保,至今還在農業生產中使用,明朝的徐光啟就對筒車模型做過研究,而且畫出了工作原理圖,這里向學生呈現我國古代勞動人民的智慧結晶,吸引學生注意力,同時使學生產生學習的興趣.
窺一斑而見全豹,在課本中貫穿很多數學文化知識,同時將數學探究與學生建模結合起來,使學生產生民族自豪感的同時,引起學生的興趣,并開闊學生的眼界,使其理解數學來源于生活,又能服務于生活.
4 數學探究、數學建模與生活息息相關
數學建模和數學探究活動與生活息息相關,可以從生活中得到課題,如研究豬肉的化凍時間與溫度的關系、跑步時體重與最佳燃脂心率的關系、鞋碼與身高的關系,等等.生活中處處有數學,在運用數學知識解決實際問題的過程中,培養學生理論與實踐相結合的能力,拓展知識面,培養學習興趣,同時增強創新意識和實踐能力.
5 結語
數學探究活動與數學建模活動不是單獨存在的,依托于整個教學內容結構的整體設計,即大單元的結構,以某種知識脈絡為主線,串聯所有知識,抽絲剝繭從知識的發生發展娓娓道來,依托數學文化建構數學模型,使學生體會生活與數學的關聯,同時可以開闊學生眼界,以模型為依托進行數學探究活動,感悟數學來源于生活.理論運用于實踐,從知識內化為能力……這樣行云流水般的設計使數學大單元的結構渾然天成,數學建模與數學探究活動穿插其中是知其然的過程,也是知其所以然的過程.
參考文獻:
[1]許小穎.大單元視角下的初中數學單元教學研究[J].數學教學通訊,2022(05):46-47.
[2]葛開順.深化高中數學建模教學,培養學生數學應用能力[J].數理天地(高中版),2023(03):86-88.
[3]張明剛.基于數學建模核心素養下的高中數學課堂研究[J].數學學習與研究,2023(01):122-124.
[4]顧向忠.關于“數學建模與數學探究”的高中數學教材比較研究——以蘇教版、人教A版和人教B版為例[J].中學數學教學參考,2022(34):13-16.
[5]陳輝忠.培養高中數學建模素養的教學探究[J].數理天地(高中版),2022(17):52-54.
[6]狄聞于.高中數學建模與核心素養的分析和探究[J].中學數學,2022(19):92-93.

