多元操作助力數(shù)學(xué)抽象

張緬

摘 要：“圓的認(rèn)識(shí)”是小學(xué)生從認(rèn)識(shí)直線平面圖形到認(rèn)識(shí)曲線平面圖形的一個(gè)轉(zhuǎn)折點(diǎn)，學(xué)生的認(rèn)知水平?jīng)Q定了他們對(duì)圓的概念本質(zhì)理解的困難。《圓的認(rèn)識(shí)》一課教學(xué)，有結(jié)構(gòu)地呈現(xiàn)數(shù)學(xué)現(xiàn)象，激活不同層次的數(shù)學(xué)心智圖像，使之互相聯(lián)結(jié)、綜合，引發(fā)學(xué)生對(duì)圓本質(zhì)的數(shù)學(xué)抽象，通過(guò)延展性操作的運(yùn)用，推進(jìn)認(rèn)知的再提升。此外，還創(chuàng)設(shè)充分的思考空間，助力學(xué)生感悟極限的數(shù)學(xué)思想；融入數(shù)學(xué)史元素，培養(yǎng)學(xué)生的文化自信。

關(guān)鍵詞：小學(xué)數(shù)學(xué)；操作；心智圖像；抽象；《圓的認(rèn)識(shí)》

一、課前思考

（一）教學(xué)內(nèi)容解讀

“圓的認(rèn)識(shí)”是蘇教版小學(xué)數(shù)學(xué)五年級(jí)下冊(cè)《圓》單元起始課的教學(xué)內(nèi)容，是在學(xué)生初步掌握常見(jiàn)直線圖形的基本特征及其周長(zhǎng)、面積公式，并且直觀認(rèn)識(shí)圓的基礎(chǔ)上進(jìn)行教學(xué)的。從直線圖形到曲線圖形，研究的方法、思想都有所變化。這一內(nèi)容的學(xué)習(xí)旨在促使學(xué)生進(jìn)一步發(fā)展空間觀念，為后續(xù)學(xué)習(xí)圓的度量以及和圓相關(guān)的立體圖形知識(shí)提供有力支撐。

就小學(xué)生的認(rèn)知水平而言，從數(shù)學(xué)本質(zhì)上認(rèn)識(shí)圓以及相關(guān)概念有一定的難度。原因有兩點(diǎn)。其一，以往研究平面圖形的經(jīng)驗(yàn)不適用。直線圖形的構(gòu)成要素外顯，學(xué)生對(duì)圖形的研究主要從點(diǎn)、邊、角等方面開(kāi)展。而圓的構(gòu)成要素內(nèi)隱，圓心、半徑、直徑等都不在圓上。其二，生活經(jīng)驗(yàn)阻礙學(xué)生深度認(rèn)識(shí)圓的本質(zhì)。圓形物體在生活中隨處可見(jiàn)，因?yàn)樘煜ぃ吹故沟脤W(xué)生對(duì)圓的認(rèn)識(shí)聚焦在“形”的特點(diǎn)上，而忽略對(duì)圓本質(zhì)的思考。這就需要教師尋求有效方法引領(lǐng)學(xué)生探索圓的本質(zhì)。

（二）學(xué)習(xí)情況分析

為了更準(zhǔn)確地了解學(xué)生知識(shí)與能力的起點(diǎn)，厘清學(xué)生對(duì)圓概念的認(rèn)知水平，我對(duì)五年級(jí)兩個(gè)班的89名學(xué)生進(jìn)行了前測(cè)。部分前測(cè)問(wèn)題和學(xué)生回答情況如下：

“你聽(tīng)說(shuō)過(guò)圓嗎？你對(duì)圓有哪些了解？你聽(tīng)說(shuō)過(guò)半徑、直徑、圓心嗎？”100%的學(xué)生聽(tīng)說(shuō)過(guò)圓；87%的學(xué)生聽(tīng)說(shuō)過(guò)圓心、半徑、直徑；23%的學(xué)生知道圓是曲線圖形；38%的學(xué)生知道圓是軸對(duì)稱圖形。

“生活中哪些物體是圓形的？”91%的學(xué)生能準(zhǔn)確說(shuō)出生活中的圓形物體。

“你會(huì)用圓規(guī)畫(huà)圓嗎？請(qǐng)你用圓規(guī)畫(huà)出一個(gè)圓。”100%的學(xué)生會(huì)用圓規(guī)畫(huà)圓，但只有25%的學(xué)生能畫(huà)得較光滑。

“你知道圓規(guī)為什么可以畫(huà)出圓嗎？”38%的學(xué)生能說(shuō)出圓規(guī)兩腳之間的距離固定，大部分學(xué)生不知道原因。

“請(qǐng)你描述什么是圓。”93%的學(xué)生描述圓的外形特點(diǎn)，如光滑、沒(méi)有角、沒(méi)有邊等，沒(méi)有學(xué)生能說(shuō)出圓的本質(zhì)特征。

“你能說(shuō)說(shuō)什么是半徑、直徑嗎？”9%的學(xué)生能說(shuō)出大概意思，11%的學(xué)生知道直徑長(zhǎng)度是半徑的兩倍，大部分學(xué)生無(wú)法說(shuō)出什么是半徑或直徑。

“關(guān)于圓，你想學(xué)習(xí)什么？”93%的學(xué)生想研究周長(zhǎng)和面積，1%的學(xué)生想研究圓的特征。

通過(guò)前測(cè)可以看出，多數(shù)學(xué)生可以在生活中辨認(rèn)出圓形物體，知道圓的外形特點(diǎn)，知道圓的相關(guān)概念的名稱；所有學(xué)生都有用圓規(guī)畫(huà)圓的經(jīng)歷；學(xué)生對(duì)圓的定點(diǎn)、定長(zhǎng)本質(zhì)沒(méi)有思考，對(duì)半徑、直徑的概念內(nèi)涵不理解，對(duì)使用圓規(guī)畫(huà)圓僅停留在機(jī)械操作階段，并未將其與圓的本質(zhì)進(jìn)行聯(lián)系；學(xué)生把對(duì)圓的生活經(jīng)驗(yàn)當(dāng)成了數(shù)學(xué)理解，缺乏對(duì)圓的特征研究的主觀意愿。

（三）教學(xué)思路確定

綜上，本課教學(xué)，我形成了三個(gè)思考方向：（1）學(xué)生自我認(rèn)定已經(jīng)“認(rèn)識(shí)”了圓，怎樣讓他們有興趣“重新認(rèn)識(shí)”圓？（2）學(xué)生已經(jīng)會(huì)畫(huà)圓，怎樣讓他們主動(dòng)發(fā)現(xiàn)畫(huà)圓的意義？（3）學(xué)生聽(tīng)過(guò)“半徑”“直徑”“圓心”，怎樣讓他們自主探索這些概念的本質(zhì)？

基于上述分析與思考，我明確了《圓的認(rèn)識(shí)》一課的教學(xué)思路。第一階段，有結(jié)構(gòu)地呈現(xiàn)圓的數(shù)學(xué)現(xiàn)象，從純天然“圓”到人工創(chuàng)作的“圓”再到運(yùn)動(dòng)中形成的“圓”，從靜態(tài)到動(dòng)態(tài)，逐步靠近圓的本質(zhì)，呈現(xiàn)圓的數(shù)學(xué)現(xiàn)象，激活不同知識(shí)儲(chǔ)備或思維水平的學(xué)生頭腦中對(duì)應(yīng)的心智圖像。第二階段，組織學(xué)生用不同方式畫(huà)圓，將他們不同概括水平的心智圖像動(dòng)態(tài)地、有層次地展現(xiàn)出來(lái)，通過(guò)諸多心智圖像的累積、調(diào)整、聯(lián)結(jié)、綜合，喚醒學(xué)生提取共性的本能。第三階段，讓學(xué)生反復(fù)地操作，不斷強(qiáng)化“現(xiàn)象—數(shù)學(xué)—現(xiàn)象”的對(duì)應(yīng)，逐步抽象出圓“一中同長(zhǎng)”的本質(zhì)。第四階段，通過(guò)操作，運(yùn)用抽象出的概念本質(zhì)處理延展性數(shù)學(xué)問(wèn)題，讓學(xué)生將演繹推理與合情推理有機(jī)結(jié)合，進(jìn)一步發(fā)展抽象能力，對(duì)概念本質(zhì)有新的認(rèn)識(shí)。如此，學(xué)生實(shí)現(xiàn)圓概念的完整建構(gòu)，也發(fā)展了實(shí)踐能力和創(chuàng)新意識(shí)。

二、課堂實(shí)踐

（一）走進(jìn)圓的世界——呈現(xiàn)豐富的數(shù)學(xué)現(xiàn)象

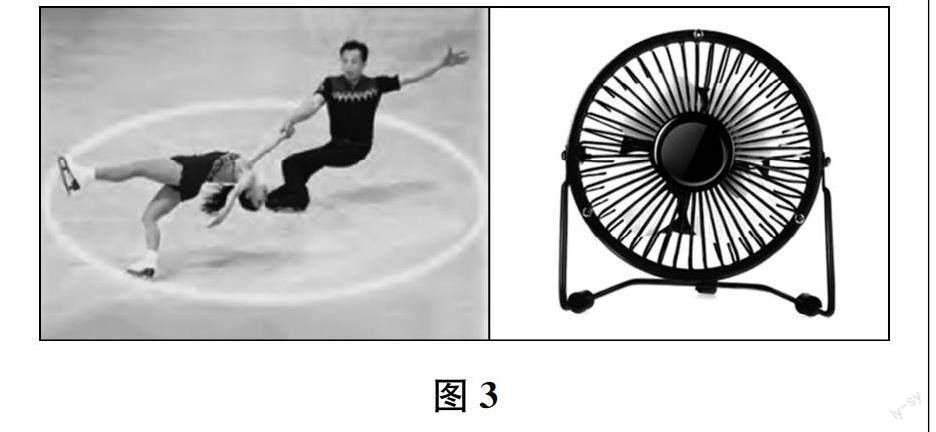
師 （出示下頁(yè)圖1）注意過(guò)這樣的自然現(xiàn)象嗎？（出示下頁(yè)圖2）欣賞過(guò)這樣的建筑物或工藝品嗎？（出示圖3）見(jiàn)過(guò)類似的運(yùn)動(dòng)嗎？世界充滿圓。畢達(dá)哥拉斯說(shuō)：一切平面圖形中最美的是圓形。從這句話中，你知道圓是什么圖形？

（學(xué)生欣賞、交流自然中關(guān)于圓的現(xiàn)象，體會(huì)圓是一種平面圖形。）

師 下面，讓我們走進(jìn)圓的世界，一起認(rèn)識(shí)圓。

［設(shè)計(jì)意圖：課始，呈現(xiàn)大量自然界和生活中的“圓”的現(xiàn)象，讓學(xué)生欣賞、辨認(rèn)。豐富的現(xiàn)實(shí)原型喚醒了學(xué)生的生活經(jīng)驗(yàn)，不僅讓學(xué)生享受圓的外在美，同時(shí)也激發(fā)學(xué)生探究圓內(nèi)在奧秘的積極心向。］

（二）嘗試圓的畫(huà)法——激活多元的心智圖像

1.自主畫(huà)圓

師 課前交流中，我發(fā)現(xiàn)同學(xué)們對(duì)圓有了不少認(rèn)識(shí)。現(xiàn)在，我們換一個(gè)角度認(rèn)識(shí)圓。小組合作，自選工具畫(huà)圓。活動(dòng)要求如下：（1）畫(huà)一畫(huà)，自主選擇工具（圓規(guī)、直尺或其他手邊工具）畫(huà)圓。（2）想一想，所選工具為什么能畫(huà)成圓。（3）談一談，在小組內(nèi)交流畫(huà)圓的感受。

教師對(duì)各小組的學(xué)習(xí)情況巡視指導(dǎo)。學(xué)生匯報(bào)交流，具體如下：

（1）借助有圓面的物體畫(huà)圓。用這種畫(huà)法的學(xué)生想到了圓的樣子，利用膠帶或水杯上的圓面，沿著邊緣描出圓。他們感覺(jué)這樣的方法畫(huà)圓很快。教師提問(wèn)：你們覺(jué)得這種方法有不足嗎？學(xué)生思考后回答：這樣只能描出固定的圓；如果要畫(huà)出不同大小的圓，則還要選擇其他工具。

（2）用直尺畫(huà)圓。用這種畫(huà)法的學(xué)生聯(lián)想到自行車輪，先畫(huà)一個(gè)點(diǎn)表示輪軸，再以它為中心畫(huà)很多一樣長(zhǎng)線段表示鋼絲，最后將這些線段的另一個(gè)端點(diǎn)連起來(lái)，就像輪胎一樣，形成了一個(gè)近似的圓。教師請(qǐng)學(xué)生簡(jiǎn)單示范，學(xué)生現(xiàn)場(chǎng)畫(huà)圖（如下頁(yè)圖4）。師生互動(dòng)，教師相機(jī)板書(shū)：定點(diǎn)、定長(zhǎng)。教師提問(wèn)：怎么得到圓呢？學(xué)生回答：畫(huà)的線段越多，端點(diǎn)就越密；要是畫(huà)無(wú)數(shù)條線段，端點(diǎn)就能連成真正的圓。教師請(qǐng)學(xué)生觀察所畫(huà)的圖形，追問(wèn)：可這個(gè)“圓”有的地方凸起來(lái)，有的地方凹進(jìn)去，這是為什么？學(xué)生思維被點(diǎn)燃，紛紛補(bǔ)充：畫(huà)得線段不一樣長(zhǎng)，并沒(méi)有都正好2 cm；畫(huà)得線段也不夠多；線段畫(huà)得不均勻，有的地方密，有的地方疏……學(xué)生表示，雖然畫(huà)不完無(wú)數(shù)條，但可以畫(huà)密些、準(zhǔn)些，就能說(shuō)明問(wèn)題；并且，通過(guò)想象、推理，這樣能得到一個(gè)均勻的圓。教師追問(wèn)：那這個(gè)圓上每個(gè)點(diǎn)到定點(diǎn)的距離都怎樣？學(xué)生異口同聲：相等。學(xué)生感受到用這種方法能畫(huà)出大小不同的圓，只要在尺上找到不同的刻度（即選擇不同的定長(zhǎng)）。

（3）用圓規(guī)畫(huà)圓。教師請(qǐng)用圓規(guī)畫(huà)圓的學(xué)生上臺(tái)畫(huà)圓并介紹畫(huà)法。學(xué)生說(shuō)，聯(lián)想到雙人滑冰的畫(huà)面（圖3左圖），圓規(guī)針尖就像男運(yùn)動(dòng)員的腳固定了圓的位置，筆尖就像女運(yùn)動(dòng)員的腳旋轉(zhuǎn)一周畫(huà)出了圓。教師追問(wèn)：為什么這樣就能畫(huà)出圓？學(xué)生討論：因?yàn)槟羞\(yùn)動(dòng)員的腳和女運(yùn)動(dòng)員的腳之間的距離沒(méi)有變過(guò)，也就是圓規(guī)兩腳之間的距離相等。學(xué)生也指出了一些同學(xué)畫(huà)得不“圓”、不光滑的原因，正是圓規(guī)兩腳之間的距離改變了。進(jìn)而提出，用圓規(guī)畫(huà)圓要捏好手柄，加強(qiáng)操作的規(guī)范性。通過(guò)交流，學(xué)生自主得到結(jié)論：圓規(guī)兩腳之間的距離固定，有了“定長(zhǎng)”，這樣就能畫(huà)出圓。教師順勢(shì)溝通畫(huà)法：用圓規(guī)畫(huà)圓和用直尺畫(huà)圓，你的感受相同嗎？學(xué)生指出：用圓規(guī)更專業(yè)、快捷；本質(zhì)上二者是相同的，都有定點(diǎn)、定長(zhǎng)，只是用圓規(guī)畫(huà)圓隱藏了無(wú)數(shù)條定長(zhǎng)的線段，直接把無(wú)數(shù)個(gè)端點(diǎn)連成曲線。

［設(shè)計(jì)意圖：在平面內(nèi)，圓是到定點(diǎn)的距離等于定長(zhǎng)的點(diǎn)的集合。用直尺畫(huà)圓這種畫(huà)法是將圓的隱形本質(zhì)可視化的絕佳方式。相較于用有圓面的物體的畫(huà)法，這類學(xué)生形成的圓的心智圖像更貼近數(shù)學(xué)本質(zhì)。及時(shí)將這樣的心智圖像作為教學(xué)資源，因勢(shì)利導(dǎo)，請(qǐng)學(xué)生現(xiàn)場(chǎng)畫(huà)圓，放慢圓的形成過(guò)程。在這樣的操作過(guò)程中，學(xué)生經(jīng)歷從數(shù)學(xué)現(xiàn)象（如不均勻、凹凸不平等）過(guò)渡到心智圖像（在腦海里不斷調(diào)整，并想象、推理）逐步走向數(shù)學(xué)本質(zhì)。學(xué)生主動(dòng)參與，積極探索，發(fā)展了空間觀念，并初步感悟了極限這一數(shù)學(xué)思想。刺激到用圓規(guī)畫(huà)圓學(xué)生的數(shù)學(xué)現(xiàn)象往往是生活中那些動(dòng)態(tài)生成的圓，這些現(xiàn)象投射在學(xué)生腦海中形成的數(shù)學(xué)心智圖像也是概括水平最高的，它們最接近圓的本質(zhì)，利于學(xué)生建構(gòu)概念。教師給予充分的空間讓學(xué)生展示和交流用圓規(guī)畫(huà)圓的方法，抓住“為什么圓規(guī)能畫(huà)出圓？” 這一關(guān)鍵問(wèn)題引發(fā)學(xué)生的數(shù)學(xué)思考，讓學(xué)生主動(dòng)將數(shù)學(xué)現(xiàn)象和數(shù)學(xué)本質(zhì)建立聯(lián)系。通過(guò)圓規(guī)畫(huà)圓與直尺畫(huà)圓的方法比較，為抽象圓“一中同長(zhǎng)”的本質(zhì)奠定基礎(chǔ)。］

2.規(guī)范畫(huà)圓

教師用圓規(guī)示范畫(huà)出一個(gè)定長(zhǎng)2 cm的圓，規(guī)范畫(huà)法。

師 定點(diǎn)在圓的什么位置？

生 中心。

師 定長(zhǎng)2 cm的線段有什么特征？

生 一端在圓心，一端在圓上。

師 像這樣的線段有多少條？

生 無(wú)數(shù)條。

師 為什么？

生 因?yàn)閳A上有無(wú)數(shù)個(gè)點(diǎn)都能和圓心連成這樣的線段。

交流互動(dòng)中揭示圓心、半徑概念以及字母表示。請(qǐng)學(xué)生畫(huà)一個(gè)半徑3 cm的圓。并用字母標(biāo)出圓心和半徑。展示幾幅作品（如圖5），觀察交流。

生 這些圓一樣大，因?yàn)榘霃较嗟取?/p>

請(qǐng)學(xué)生在剛才畫(huà)的圓基礎(chǔ)上，保持圓心不變，再畫(huà)一個(gè)不同的圓。再展示幾幅作品（如圖6），觀察交流。學(xué)生聯(lián)想到水波擴(kuò)散與樹(shù)木年輪圖片（圖1），發(fā)現(xiàn)半徑變短，圓變小；半徑變長(zhǎng)，圓變大。將兩次作品放在一起，再次組織觀察、交流感受。學(xué)生明確：半徑?jīng)Q定圓的大小，圓心決定圓的位置。

師 同學(xué)們，通過(guò)剛剛的學(xué)習(xí)，我們已經(jīng)認(rèn)識(shí)了圓心、半徑，知道了圓心決定圓的位置，半徑?jīng)Q定圓的大小。

［設(shè)計(jì)意圖：通過(guò)示范畫(huà)圓，一方面讓學(xué)生明確用圓規(guī)畫(huà)圓時(shí)需要注意的關(guān)鍵環(huán)節(jié)；另一方面，畫(huà)圓過(guò)程中，定點(diǎn)（圓心）和定長(zhǎng)（半徑）自然出現(xiàn)，互動(dòng)交流中，圓心、半徑概念的本質(zhì)呼之欲出。通過(guò)操作，學(xué)生關(guān)注的不再是概念的名稱，而真正理解了概念的內(nèi)涵。接著，學(xué)生分別在不同的紙上畫(huà)相同半徑的圓和以相同的圓心畫(huà)不同半徑的圓。兩次畫(huà)圓，一方面鞏固了學(xué)生規(guī)范的畫(huà)圓方法；另一方面，將不同學(xué)生的作品巧妙地同屏展示，形成數(shù)學(xué)現(xiàn)象，引發(fā)交流反思，不同的心智圖像在積累中組合，漸漸概括出半徑、圓心的作用。在這個(gè)操作活動(dòng)中，學(xué)生再次回到一開(kāi)始展示的水波擴(kuò)散與樹(shù)木年輪圖片，促進(jìn)“生活（現(xiàn)象）—數(shù)學(xué)—生活（現(xiàn)象）”的反復(fù)對(duì)應(yīng)，加深概念的理解。］

（三）體會(huì)圓“一中同長(zhǎng)”——完成深度的數(shù)學(xué)抽象

教師給每位學(xué)生準(zhǔn)備一張圓形紙片，請(qǐng)他們用圓規(guī)在作業(yè)本上畫(huà)出一個(gè)與之同樣大小的圓。活動(dòng)要求如下：（1）畫(huà)一畫(huà)，想辦法用圓規(guī)畫(huà)一個(gè)與圓形紙片一樣大的圓。（2）想一想，畫(huà)圓過(guò)程中，你還發(fā)現(xiàn)了什么。（3）說(shuō)一說(shuō)，把你的想法在小組內(nèi)交流。

學(xué)生提出“先找半徑”的觀點(diǎn)。有的學(xué)生把圓片對(duì)折、再對(duì)折找到圓心，連接圓心和圓上任意一點(diǎn)得到半徑。有的學(xué)生把圓片對(duì)折一次，用尺子測(cè)量折痕所在線段的長(zhǎng)度，找到線段的中點(diǎn)，由這個(gè)點(diǎn)到圓上一點(diǎn)的長(zhǎng)度得到半徑長(zhǎng)。

通過(guò)對(duì)比，學(xué)生發(fā)現(xiàn)不管用什么方法找半徑都要先找到圓心。教師組織學(xué)生討論為什么。學(xué)生交流：因?yàn)榘霃接袃蓚€(gè)端點(diǎn)，一個(gè)端點(diǎn)在圓上，圓上任意一點(diǎn)都可以；另一個(gè)端點(diǎn)在圓心，圓心只有一個(gè)，在圓的中心，所以關(guān)鍵在確定圓片的圓心。

教師引導(dǎo)學(xué)生再研究圓片，學(xué)生發(fā)現(xiàn)自己的圓片上均出現(xiàn)了一些折痕，這些折痕很有特點(diǎn)。教師請(qǐng)學(xué)生用不同顏色的筆畫(huà)出兩條折痕（如下頁(yè)圖7），并與同桌一起研究。學(xué)生交流：這些折痕經(jīng)過(guò)圓心，兩端都在圓上；長(zhǎng)度是半徑的兩倍，可以通過(guò)折或量得出；這樣的折痕有無(wú)數(shù)條；圓是軸對(duì)稱圖形，折痕所在的直線是它的對(duì)稱軸……教師順勢(shì)指出：這樣的線段叫作直徑，直徑用字母d表示，直徑和半徑的關(guān)系怎么表示？d=2r和r=d/2一位學(xué)生拿出一個(gè)小號(hào)圓片，將其直徑和原來(lái)圓片的半徑比較，提出質(zhì)疑：我這個(gè)圓的直徑怎么不是半徑的兩倍？同伴補(bǔ)充：這樣的關(guān)系要在同一個(gè)圓中。

師 回顧這節(jié)課的兩次活動(dòng)，你有什么收獲？

生 研究了圓心、半徑、直徑，知道了它們的特征以及半徑和直徑之間的關(guān)系，學(xué)會(huì)了規(guī)范地畫(huà)圓。

師 中國(guó)古代科學(xué)家墨子這樣概括圓的特征：“圓，一中同長(zhǎng)也。”你能解讀一下這句話嗎？

生 “一中”，一個(gè)圓心；“同長(zhǎng)”，半徑（直徑）等長(zhǎng)。

師 中國(guó)古人充滿了智慧，4個(gè)字就概括了圓的本質(zhì)。

［設(shè)計(jì)意圖：讓學(xué)生畫(huà)一個(gè)和圓形紙片同樣大的圓，學(xué)生通過(guò)操作找到圓心，逆向理解半徑的內(nèi)涵。抓住操作中的生成性資源——折痕開(kāi)展研究，直徑概念的內(nèi)涵、特征以及直徑與半徑的關(guān)系自然建構(gòu)。通過(guò)小圓片直徑與大圓片半徑的對(duì)比，完善了學(xué)生對(duì)概念外延的理解。通過(guò)對(duì)比不同的作品和畫(huà)法，激發(fā)學(xué)生想象和推理。至此，那些不斷積累的圓的心智圖像在多向聯(lián)結(jié)作用下綜合，形成完整的圓的概念，實(shí)現(xiàn)對(duì)圓本質(zhì)的深度抽象。另外，中國(guó)數(shù)學(xué)傳統(tǒng)文化的介紹，也讓學(xué)生體會(huì)到我國(guó)古代勞動(dòng)人民的偉大智慧，提升文化自信。］

（四）綜合應(yīng)用圓的本質(zhì)——引發(fā)知識(shí)再認(rèn)識(shí)的延展性操作

師 給你一條線段AB，你能畫(huà)一個(gè)圓，使圓周經(jīng)過(guò)線段端點(diǎn) A、B嗎？

大部分學(xué)生認(rèn)為：應(yīng)以線段AB的中點(diǎn)為圓心，線段AB的一半長(zhǎng)度為半徑，只能畫(huà)出一個(gè)圓。教師鼓勵(lì)學(xué)生思考是否有不同的方法。有學(xué)生想到：線段AB的垂直平分線上任意一點(diǎn)都可以作為圓心O；點(diǎn)O、點(diǎn)A、點(diǎn)B形成等腰三角形，等腰三角形的腰OA作為半徑。學(xué)生思路激活，認(rèn)為可以畫(huà)出多個(gè)圓，甚至無(wú)數(shù)個(gè)圓（如圖8）。

師 課要結(jié)束了，但對(duì)圓的研究沒(méi)有結(jié)束，圓里還有太多的秘密等著我們探索挖掘。

［設(shè)計(jì)意圖：延展性練習(xí)，充分挖掘“做”與“思”的空間，引發(fā)學(xué)生開(kāi)展不同層次的操作。首先，學(xué)生通過(guò)剛才習(xí)得的知識(shí)和方法進(jìn)行演繹推理，初步解決問(wèn)題，獲得成功喜悅。接著，教師進(jìn)一步啟發(fā)，鼓勵(lì)學(xué)生對(duì)成果進(jìn)行拓展，將問(wèn)題吊到半空，觸發(fā)學(xué)生“跳一跳，摘果子”。新一輪操作把學(xué)生思維引向“最近發(fā)展區(qū)”，結(jié)論從一個(gè)圓到多個(gè)圓再到無(wú)數(shù)個(gè)圓，實(shí)現(xiàn)新的突破。］

三、課后反思

（一）提供遞進(jìn)式操作路徑，促進(jìn)認(rèn)知發(fā)展

本課設(shè)計(jì)了兩個(gè)以“畫(huà)圓”為主線的大活動(dòng)。

第一次“畫(huà)圓”分三個(gè)層次展開(kāi)：層次一，學(xué)生自主畫(huà)圓，以問(wèn)題“為什么能畫(huà)成圓”勾連學(xué)生的不同畫(huà)法，展示不同層次的心智圖像，將數(shù)學(xué)現(xiàn)象與數(shù)學(xué)本質(zhì)主動(dòng)建立聯(lián)系。層次二，教師示范畫(huà)圓，邊畫(huà)邊談“定點(diǎn)在什么位置”“定長(zhǎng)的線段有什么特征”，圓心、半徑的內(nèi)涵呼之欲出，對(duì)概念的認(rèn)識(shí)逐步聚焦圓的本質(zhì)。層次三，學(xué)生畫(huà)指定的圓，對(duì)比不同學(xué)生的作品，圓心、半徑的作用自然浮現(xiàn)。

第二次“畫(huà)圓”，讓學(xué)生用圓規(guī)畫(huà)一個(gè)和圓片一樣大的圓。活動(dòng)分兩條線索展開(kāi)：明線，在紙上畫(huà)圓；暗線，在圓片上找圓心和半徑。走明線就必定經(jīng)過(guò)暗線，也就必然留下“痕跡”，為學(xué)生自主探究直徑及抽象出圓的本質(zhì)及相關(guān)概念，提供了鮮活的素材。

全課由大大小小的數(shù)學(xué)操作活動(dòng)有機(jī)串聯(lián)，在抽絲剝繭中推動(dòng)學(xué)生對(duì)圓的認(rèn)識(shí)的發(fā)展。學(xué)生在做中思，思后再做，操作層層遞進(jìn)，思維不斷提升。

（二）創(chuàng)設(shè)充分的思考空間，助力思想感悟

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》（以下簡(jiǎn)稱“新課標(biāo)”）指出：為學(xué)生提供豐富的問(wèn)題情境、充分的思考空間，讓學(xué)生經(jīng)歷觀察、實(shí)驗(yàn)、猜測(cè)、推理、交流、反思等數(shù)學(xué)活動(dòng)過(guò)程，幫助學(xué)生感悟基本思想，積累基本活動(dòng)經(jīng)驗(yàn)。^［1］

本課創(chuàng)設(shè)的自主畫(huà)圓環(huán)節(jié)，教師開(kāi)放操作與思考的空間，讓學(xué)生自由選擇手邊的工具畫(huà)圓，這就有了生成“用直尺畫(huà)圓”的可能性。這個(gè)畫(huà)法的誕生相當(dāng)于學(xué)生自己找到了探索圓本質(zhì)的“腳手架”。教師抓住這一生成性資源，讓學(xué)生動(dòng)態(tài)展示圓的形成過(guò)程，線從少到多、點(diǎn)由疏到密、形由不像圓到像圓，在多個(gè)“越來(lái)越……”的過(guò)程中，極限思想自然滲透。即使學(xué)生最終也沒(méi)看到標(biāo)準(zhǔn)的圓，但圓的本質(zhì)已扎根于學(xué)生的想象、推理中。直至后續(xù)出現(xiàn)了用圓規(guī)畫(huà)圓，學(xué)生的猜測(cè)、推理得到進(jìn)一步驗(yàn)證，逐步進(jìn)行概括。在這樣遞進(jìn)的數(shù)學(xué)探索過(guò)程中，學(xué)生感悟了極限的數(shù)學(xué)思想。

（三）融入數(shù)學(xué)史元素，培養(yǎng)文化自信

新課標(biāo)強(qiáng)調(diào)：注重情境素材的育人功能，如體現(xiàn)中國(guó)數(shù)學(xué)家貢獻(xiàn)的素材，幫助學(xué)生了解和領(lǐng)悟中華民族獨(dú)特的數(shù)學(xué)智慧，增強(qiáng)文化自信和民族自豪感。^［2］

本課引用“圓，一中同長(zhǎng)也”（《墨子》），高度概括圓的本質(zhì)，將數(shù)學(xué)史元素自然融入教學(xué)，讓數(shù)學(xué)課堂更有溫度。這也向?qū)W生滲透了中國(guó)傳統(tǒng)文化的精髓，啟發(fā)學(xué)生在“從整體知識(shí)體系中提煉出圓的數(shù)學(xué)本質(zhì)，發(fā)展抽象思維水平”的同時(shí)，參悟古人智慧，提升文化自信，堅(jiān)定愛(ài)國(guó)情懷。

參考文獻(xiàn)：

［1］［2］ 中華人民共和國(guó)教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）［S］.北京：北京師范大學(xué)出版社，2022：94，87.