讓幾何直觀自然生長

徐亞飛

［摘? 要］ 幾何直觀主要是指運用圖表描述和分析問題的意識與習慣.能夠感知各種幾何圖形及其組成元素，依據圖形的特征進行分類；根據語言描述畫出相應的圖形，分析圖形的性質；建立形與數的聯系，構建數學問題的直觀模型；利用圖形分析實際情境與數學問題，探索解決問題的思路.

［關鍵詞］ 圓周角；幾何直觀；猜想；驗證

“幾何直觀”是《義務教育數學課程標準（2022年版）》提出的核心素養主要表現之一，幾何直觀主要是指運用圖表描述和分析問題的意識與習慣. 能夠感知各種幾何圖形及其組成元素，依據圖形的特征進行分類；根據語言描述畫出相應的圖形，分析圖形的性質；建立形與數的聯系，構建數學問題的直觀模型；利用圖形分析實際情境與數學問題，探索解決問題的思路. 幾何直觀有助于學習者把握問題的本質，明晰思維的路徑.

活動一：情境引入，發現新知

課前播放足球射門的精彩瞬間的視頻.

思考：如圖1，在足球比賽場上，甲、乙兩名隊員互相配合向對方球門MN進攻，當甲帶球沖到A點時，乙已跟隨沖到B點. 從射門角度看，此時甲是自己射門好，還是將球傳給乙，讓乙射門好？

設計說明? 踢足球是學生比較喜歡的一項體育運動，從學生喜愛的足球引入新課，激發了學生學習數學的熱情，調動了學生學習數學的積極性. 通過欣賞足球射門的視頻，學生感受到數學與自己的生活息息相關、不可分割，同時也感受到數學的魅力無處不在.

活動二：復習回顧，引入新知

復習回顧圓心角的定義（頂點在圓心的角叫作圓心角）及其性質（圓心角的度數等于其所對弧的度數）.

思考1：改變圓心角的頂點P的位置，這個點P除了在圓心，還可以在哪些位置呢？（圓內、圓上、圓外）

思考2：嘗試給這三個角命名. （圓內角、圓周角、圓外角）

由此引出今天的課題“圓周角”.

設計說明? 復習回顧圓心角的定義和性質，通過改變圓心角頂點P的位置，自然而然地引入了圓內角、圓周角以及圓外角，讓學生感受到數學知識前后的連續性.

活動三：類比學習，探究新知

（一）圓周角的概念

思考1：類比圓心角的學習，圓周角將從哪些方面來學習？（定義、性質等）

思考2：對于頂點在圓周上的角，改變角的兩邊與圓的位置關系（如圖2、圖3），得到另兩類頂點在圓周上的角，判斷這兩類角是否是圓周角.（不是）

思考3：根據黑板上的圖形以及你對圓周角的理解，嘗試給出圓周角的概念（頂點在圓周上，兩邊與圓相交的角）

判斷：如圖4，∠P是圓周角嗎？（是，角的兩邊是射線）

思考4：回憶圓心角的定義（頂點在圓心的角），為什么圓心角的定義只要滿足一個條件，而圓周角的定義卻要滿足兩個條件？

設計說明? 根據圓周角的圖形，讓學生自行歸納出圓周角的定義，培養學生的語言表達能力和自主學習的能力. 區別圓心角和圓周角定義的不同，加深學生對概念的理解.

練習：如圖5，弧CD所對的圓周角是______；

∠ACB所對的弧是______；

弦BD所對的圓周角是______.

設計意圖? 通過這道題目，讓學生感受一條弧所對的圓周角不止一個，但一條弧所對的圓心角卻只有一個，進而引導學生發現一條弦所對的圓周角也有無數個，且可以分為兩類.

設計說明? 通過類比圓心角的學習過程來探究圓周角的學習過程，培養學生自主學習的能力. 圓周角的概念比圓心角的概念多了一個條件“角的兩邊與圓相交”，通過一組題目讓學生感受為什么要加上這樣一個限制條件，以加深學生對圓周角概念的理解.

（二）圓周角的性質

猜想1：同弧所對的圓周角相等.

實驗驗證1：幾何畫板驗證“同弧所對的圓周角相等”.

通過幾何畫板的演示，我們發現同弧所對的圓周角相等.

思考：同弧所對的圓周角為什么會相等？（相等的圓周角所對的弧是同一條弧）

設計意圖? 通過畫圖、度量、猜想、幾何畫板驗證，讓學生初步感知“同弧（等弧）所對的圓周角相等”，通過改變弧的長度，讓學生再次感受圓周角的大小與其所對的弧有著密切的聯系.

猜想2：同弧所對的圓周角的度數是圓心角度數的一半.

實驗驗證2：幾何畫板驗證“同弧（等弧）所對的圓周角的度數是圓心角度數的一半”.

設計意圖? 通過畫圖、度量、猜想、幾何畫板驗證，讓學生初步感知“同弧（等弧）所對的圓周角的度數是圓心角度數的一半”.

對于這兩個猜想，我們用幾何畫板進行了驗證. 當然，要說明這兩個猜想是正確的，必須要給出數學證明.

我們先來證明第二個猜想：同弧所對的圓周角的度數是圓心角度數的一半.

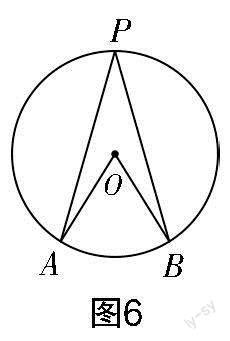
教師展示如圖6所示的圖形（來源于學生）：

思考1：大家所畫的圓周角和圓心角的位置關系和這幅圖一樣嗎？

投影儀展示學生的不同畫法（如圖7、圖8）.

思考2：三幅圖的不同點在哪里？（圓周角和圓心角的位置不同）.

思考3：大家想先證明哪一幅圖？

我們在研究一類圖形的時候，常常是從特殊到一般. 圖7最為簡單，用外角即可解決. 圖6、圖8均可通過添加適當的輔助線轉化為圖7來解決，也就是我們常說的把未知的知識轉化成已有的知識來解決，當然，我們也可以用已有的知識去探究未知的知識.

設計說明? 讓學生經歷動手操作、觀察、猜想、實驗、推理等過程，一步步地來探究圓周角的性質，培養學生獨立分析問題、解決問題的能力. 兩個猜想，到底先證明哪一個呢？其實只要證明了“同弧所對的圓周角的度數是圓心角度數的一半”，就能得到“同弧（等弧）所對的圓周角相等”. 對于“同弧所對的圓周角的度數是圓心角度數的一半”的證明，又要分三種情況來討論，這也是本節課的一個難點：①為什么要分類？②分類依據是什么？③三種情況又分別如何證明？教師層層引導，激發學生的思維活力.

活動四：課堂小練，鞏固新知

思考：在同圓或等圓中，同弧所對的圓內角、圓周角、圓外角之間的大小關系如何？（如圖12）

在同圓或等圓中，同弧所對的圓內角>圓周角>圓外角.

設計說明? 通過一組題目的訓練，既夯實了本節課的兩個重要的知識點，又為接下來引出圓周角、圓外角以及圓內角之間的大小關系做好鋪墊，更為接下來解決“情境引入環節”遺留的“足球問題”埋下伏筆.

活動五：情境再現，學以致用

思考：如圖13，在足球比賽場上，甲、乙兩名隊員互相配合向對方球門MN進攻，當甲帶球沖到A點時，乙已跟隨沖到B點. 從射門角度看，此時甲是自己射門好，還是將球傳給乙，讓乙射門好？

設計說明? 再次回到課前的情境引入，不難發現之前的難題已經迎刃而解. 讓學生意識到學習數學就是為了解決生活中所遇到的一些問題，由此激發學生學習數學的積極性.

活動六：課堂小結，提升新知

（1）圓周角有何特征？與圓心角有何異同點？（2）在證明圓周角定理時，你積累了哪些重要的方法？（3）你還有哪些疑惑？

設計說明? 通過一組問題串，進行有針對性的課堂小結，幫助學生梳理本節課的知識要點，構建本節課的知識框架，提升本節課的思想方法，培養學生的自主學習能力，提升學生良好的學習品質.

教學反思

本節課設計了三個環節：第一個環節是圓周角概念的得出. 從學生熟悉的足球射門入手，并埋下伏筆，激發學生學習新知的欲望，提高學生學習數學的積極性，同時也讓學生感受到生活中處處都有數學. 通過復習圓心角的概念和性質，幫助學生回憶圓心角的學習過程，進而引導學生發現：圓周角的學習可以類比圓心角的學習過程來進行. 第二個環節是探究圓周角定理. 通過學生的動手操作：先畫再度量，最后猜想并驗證，讓學生經歷動手操作、思考探究、歸納猜想、理論證明等一系列學習過程，培養學生的綜合能力. 在證明“圓周角的度數等于它所對弧的圓心角度數的一半”這個定理時，沒有直接給出三種類型，而是讓學生在自我實踐中發現：這個圖形有多種可能性，必須分類討論，從而培養學生分析問題和解決問題的能力. 第三個環節就是學以致用. 用今天所學的內容來解決與圓周角有關的問題，從而解決了課前情境引入中的足球射門的問題，讓學生感受到數學來源于生活，又服務于生活！

借助幾何直觀，通過自主探索、發現和再創造，讓學生體驗數學創造性的學習歷程，激發學生的創造熱情，使學生形成良好的思維品質. 弗賴登塔爾曾說過：“幾何直觀能告訴我們什么是可能重要、可能有意義和可接近的. ”運用幾何直觀，學生的思維便有了一定的載體，不再空洞乏味，由此加深學生對知識的理解，激發學生對數學學習的熱情，從而邁向數學學習的最終目標：讓學習者學會用數學的眼光觀察現實世界，學會用數學的思維思考現實世界，學會用數學的語言表達現實世界.