讓神奇的“轉化”有效滲透

周小蘇

【摘 要】數學思想方法是數學核心素養的核心，是數學學習的靈魂，也是處理數學問題的指導思想和基本策略。數學新課標明確指出，要使學生理解和掌握基本的數學思想和方法，可見其在數學學習中具有舉足輕重的地位。轉化是一種重要的解決問題的思想方法，在小學數學中有著廣泛的應用。它是把需要解決的問題，通過某種手段，轉變成能夠解決或比較容易解決的問題，通過對新問題的求解，來解決原問題。在數學學習的過程中，教師要引導學生使用轉化的思想解決問題。

【關鍵詞】轉化 數學思想方法 小學教學

作為小學數學教師，我們深有感觸的是學生學習過的知識很容易被遺忘，而且，在生活和工作中真正能夠得到應用的數學知識并不是太多。那么，通過數學學習讓學生終身受益的究竟是什么？日本著名數學教育家米山國藏認為，是數學的精神、思維方法、研究方法、推理方法和看問題的著眼點，等等。對此，我們可以理解成盡管許多數學知識被遺忘了，但學生在數學學習中形成的核心素養卻會對其生活和工作起著深遠的影響。數學思想方法是數學核心素養的核心，它是數學學習的靈魂，也是處理數學問題的指導思想和基本策略。在教學中有意識地滲透數學思想方法，可以使學生自覺地將知識轉化為能力，從而形成核心素養。

轉化是小學數學教學中一種重要的解決問題的思想方法，它是把需要解決的問題，通過某種手段，將其變成能夠解決或比較容易解決的問題，通過對新問題的求解，來解決原問題。曹沖稱象、愛迪生測算燈泡的容積等都是運用轉化解決實際問題的經典案例。轉化在小學數學教學中有大量的應用，在數與代數、圖形與幾何等領域，轉化思想幾乎貫穿始終。善于使用轉化的思想解決問題，是學生數學思維能力發展的重要特點。下面筆者就如何讓轉化的思想方法在小學數學教學中進行有效滲透談一談自己的幾點思考。

一、學貴有困，困而后疏

（一）問題引發沖突

轉化實際上就是換個角度想問題。如化繁為簡、化新為舊、化難為易、化數為形、化異為同……所有適合用轉化思想解決的問題都有一個共同的特點：用常規方法不能或不方便解決。不憤不啟，不悱不發。在教學中，需要讓學生先有“山重水復疑無路”的困頓，才會有轉化之后“柳暗花明又一村”的疏朗，這個過程也是讓學生體會“為什么要轉化”的絕佳時機。因此，教師要善于利用問題引發沖突，讓學生在思而未果、求而不得的狀態下試圖另辟蹊徑，才是轉化的正確打開方式。

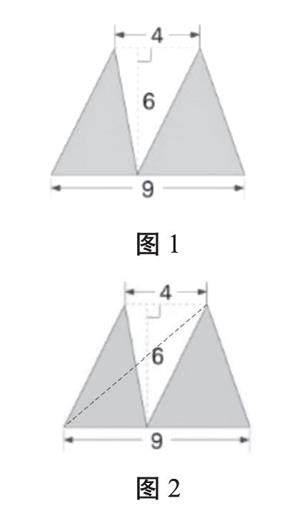
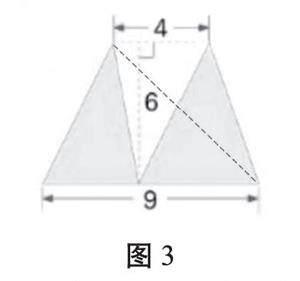
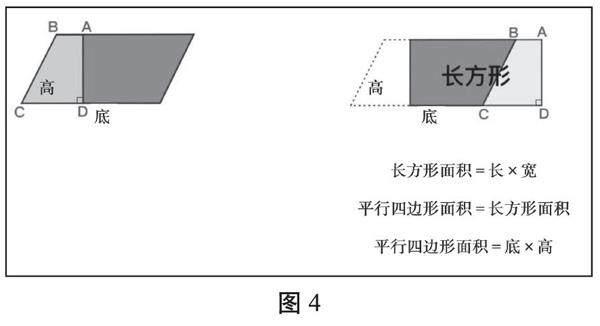
例如，求圖1中涂色部分的面積（單位：cm），當教師出示圖1后，學生發現如果用“分別求出兩個涂色三角形的面積再求和”的常規方法在這里顯然不太適合。學生思考后，發現可以轉化成“用梯形面積減掉空白三角形面積”來計算。接著，教師可以繼續發問：你還有別的方法嗎？學生在教師的追問下進入“憤”“悱”的狀態，教師適時點撥，讓學生發現此題可以通過添加輔助線，將圖1轉化成圖2和圖3，將兩個分開的涂色三角形轉化成面積相等的一個大三角形，問題就被輕松解決了。

由此可見，沒有沖突，就不會有豁然開朗、茅塞頓開的感覺。困頓和沖突越強烈，學生對轉化的需求也就越強烈，對轉化優勢的體會才會更充分。

（二）經歷增強體驗

沖突導致的困頓激發了學生強烈的探究欲望，這時放手讓學生通過經歷增強體驗就顯得尤為重要。在數學學習的過程中，無論是概念的形成、性質或定理的得出，還是思想方法的感悟和體會，都離不開學生親歷完整的學習過程。任何一種灌輸式的教學都是行不通的。轉化作為一種數學思想方法，其本身具有的內隱性更決定了學生需要在學習中不斷通過觀察、比較、分析、綜合、歸納、概括、實驗等手段親身經歷數學知識的形成過程，在獲得對問題的認識、理解和解決的同時，才能獲得對數學思想方法的認識和感悟。

例如，平行四邊形面積公式的推導。（見圖4）

學生在以上的過程中需要不停地進行觀察、比較、分析、歸納、概括……才能在長方形面積計算的基礎上“生長”出平行四邊形面積計算的公式。如果沒有充分的經歷，而只是由教師告知一個簡單的結論，那學生對轉化的思想方法就沒有任何體驗和感悟。

二、學貴好悟，悟而后明

（一）表達激活思維

數學思想方法是數學思維活動后產生的結果，是對數學知識發生過程的升華，是數學思維的結晶。因此，數學思維活動的質量直接影響著學生數學思想方法的形成。語言是思維的外殼，課堂上通過讓學生對學習過程進行個性化的表達，就是在激活其主動思維、深層思維。例如，在平行四邊形面積公式推導前，教師可以引導學生就“平行四邊形的面積應該怎樣計算”展開積極思考和充分表達；在公式推導過程中可以就“怎樣將平行四邊形轉化成長方形”“轉化前后的平行四邊形和長方形有怎樣的關系”“你有什么發現”等問題進行表達；公式推導之后，又可以引導學生完整地說一說“平行四邊形面積計算公式是怎樣推導出來的”。

在引導學生進行表達的過程中，教師需要激活的是每一個學生的思維。因此，教師要想盡一切辦法將表達的重心下移，通過“同桌互說”“小組交流”“集體交流”等多種方式“逼”著學生表達。只有這樣，個性化的表達才能展現個性化的思維，學生對思想方法的感悟也在不知不覺中進行。

（二）反思加深體悟

反思，是回頭、反過來思考的意思。學生通過對學習過程進行反思，不僅可以加深對所學知識的理解，使學習能力得以提升，還可以使隱含在數學知識中的思想方法更加清晰，實現逐步抽象、概括、凝練的過程。因此，轉化的思想方法在小學數學教學中進行有效滲透，要抓住反思這一有效手段，讓學生在過程中體會其意義和價值，養成自覺、冷靜反思的好習慣，并能緊扣重要環節，思考轉化的思想方法如何在問題解決的過程中發揮關鍵作用，從而對轉化的本質意義有更深入、全面的感悟。一般來說，對于轉化的思想方法，學生可以在問題解決之后從“為什么需要轉化”“具體怎樣轉化”“轉化后怎么樣”三大問題入手進行反思。長此以往，學生對需要用轉化來解決的問題會有“類”的大致印象，對問題解決時是應該化曲為直、化繁為簡、化數為形等都有自己的直接的、經驗型的判斷，在加深體悟的基礎上主動轉化的意識也得以加強。

三、學貴梳理，理而后清

（一）回顧感受價值

當高年級的學生在對轉化有了深刻的感悟和認識后再回顧整個學習過程，會發現在數的運算、幾何圖形的面積、體積計算等內容的學習過程中，轉化幾乎無處不在，它幫助解決了許多原本無從下手的問題。例如，在學習“異分母分數加、減法”時我們將其轉化成“同分母分數加、減法”；“小數乘法”轉化成了“整數乘法”；“除數是小數的除法”轉化成“除數是整數的除法”；“多邊形的內角和”轉化成“計算多個三角形的內角和的總和”，等等。通過回顧，學生不僅在主動溝通知識間的聯系，更是以轉化的思想方法為軸，串起了一條知識鏈，對轉化的感悟自然更為深刻。最為重要的是，轉化在小學數學中的廣泛應用讓學生充分感受到其價值所在。

（二）整理明晰特征

學生數學能力和素養的提升，離不開整理和復習這一重要的方式。通過整理和復習，學生頭腦中數學認知結構會逐漸完善，也能使隱含在不同數學內容中的同一數學思想方法更加明晰，從而在得到結論的同時，讓學生感受到數學思想方法的實用性，提升學生的數學核心素養。因此，在一個單元或一個階段的學習之后，對知識進行適度的整理與復習是十分必要的。在與轉化思想方法相關知識的整理過程中，一是要努力引導學生通過回憶交流在頭腦中再現知識的形成過程。二是在整理與復習時要注意強化數學知識之間的內在聯系，幫助學生以思維導圖的形式進行梳理，并且突出數學知識形成過程中的共性。

例如，總復習“平面圖形的面積計算”可以進行整理（如圖5）：

引導學生梳理這樣的思維導圖其實就是一個再現知識形成的過程，學生要一邊梳理一邊將推導過程進行完整的表述，在梳理完畢后加深體會整個平面圖形面積計算公式推導過程都是在用轉化的思想分析和解決問題。同樣，立體圖形的體積計算公式推導也是類似的。

四、學貴善用，用而后啟

（一）應用養成自覺

數學來源于生活，又應用于生活。學生在數學學習過程中獲得的知識、能力都要在實際應用中才能得到鞏固和提升，數學思想方法也需要在實際應用中得到提煉。

在教學中，教師要注意引導學生自覺地應用轉化的思想方法，將陌生的、未知的、復雜的問題向熟悉的、已知的、簡單的問題轉化，突出轉化的思想方法對解決問題的指導作用。同時，更要引導學生在經歷完整解題過程的基礎上，充分感悟轉化思想對解決問題的指導作用，也體驗到解決問題的具體方法向轉化思想的轉變過程，強化學生的感悟。

例如，修路隊修一條路，第一天修了全長的2/7，第二天與第一天所修路程的比是2∶1，還剩500米沒修，問這條路全長多少米？

此題中既有分率又有比，應用轉化既可以把比轉化成分率，按分數實際問題來解答：第二天就是第一天的，也就是全長的×=，這樣兩天已修全場的，500米對應全長的，全長為500÷=3500（米）；也可以把分數轉化成比，借助“份數”將問題轉化成整數問題來解答。第一天修了兩份，第二天與第一天的比是2∶1，說明第二天修了4份，那500米對應全長7份中的1份，全長為500×7=3500（米）。

在實際問題的解決過程中，學生能夠明顯感知到轉化的魅力，化繁為簡、化難為易的過程讓學生體驗到了思維的樂趣。久而久之，自覺應用轉化的思想方法解決實際問題的意識也就得以養成。

（二）內化促進提升

數學思想方法的感悟內化是一個漫長的過程，不可能一蹴而就，教師和學生都要有足夠的耐心，才能在教學中實現轉化思想方法的逐漸內化，學生的核心素養也才能有效提升。一是教師要對轉化思想方法的有效滲透做長期的設計和規劃，遵循學生思維發展的潛在規律，科學地、循序漸進地進行滲透，促進有效內化；二是教師要成為有心人，善于捕捉隱藏在教學內容中適合用轉化解決的問題，有計劃、有方法地引導學生充分實踐和感知；三是教師要充分利用好反思和整理復習的有效手段促進內化。

綜上所述，問題沖突、完整經歷、多元表達、深刻反思、及時回顧、系統整理、實踐應用、主動內化是實現小學數學教學中轉化思想滲透的有效環節和手段，它們就像鏈條一樣串起學生學習的整個過程，為學生數學核心素養的發展提供保障。

【參考文獻】

[1]陳祥彬.在小學數學教學中滲透數學思想方法[J].課程·教材·教法，2010（7）.

[2]吳正憲.感悟數學思想，積累數學活動經驗——從修訂后的數學課程標準的兩個案例說起[J].基礎教育課程，2012（1）.