作圓中輔助線的三種技巧
呂士霞

【摘要】在解決平面幾何中圓的問題時,往往需要適當地添加輔助線幫助解題.從本質上說,作輔助線的目的是把復雜圖形簡單化,在已知條件和未知條件之間搭起橋梁.本文以幾道例題為基礎,談作圓中輔助線的幾種技巧.
【關鍵詞】平面幾何;初中數學;輔助線
圓是初中平面幾何中較為特殊的一種圖形.在解題時,除了要抓住其定義,還要能夠熟練運用與圓有關的性質.一般來說,圓的半徑、弦等都是經常作為輔助線的對象.下面詳細介紹幾種技巧.
技巧1 圓中有弦,作弦心距
此方法的意思是,當問題中需要對圓中弦的長度或者與弦有關的其他量求解時,作垂直于弦的半徑或者直徑,并且連接過弦端點的半徑.之后利用垂徑定理,即弦心距平分弦的性質.之后將已知的數據代入直角三角形或者矩形等特殊圖形,利用勾股定理求解出相關量的大小.
評析 對于圓中與弦有關的問題,常規解題方法就是作弦心距,構造直角三角形,利用勾股定理求解.此直角三角形的三條邊分別是:圓的半徑,弦心距,弦.這樣就可以建立三者之間的聯系.
技巧2 圓中有直徑,作直徑所對的圓周角
若題目中出現“直徑”,就需要作直徑的圓周角.在圓中,直徑所對應的圓周角為直角,反之亦成立.由此就得到一個直角三角形,結合勾股定理、銳角三角函數等知識點進行進一步計算,從而得到問題的答案.
例2 如圖2所示,線段AB是圓O的直徑,在弦AC的延長線取一點D,滿足CD=AC,線段DB的延長線交圓O于點E.
(1)求證:CD=CE;
(2)連接AE,若∠D=25°,求∠BAE的度數大小.
解 (1)證明 如圖2所示,連接BC.
因為AB是圓O的直徑,依據圓中直徑所對的圓周角為直角的性質,
所以∠ACB=90°,即BC⊥AD,
因為CD=AC,
所以AB=BD,
所以∠A=∠D,
因為∠CEB=∠A,
所以∠CEB=∠D,
所以CD=CE.
(2)如圖2所示,連接AE.
因為∠ABE=∠BAC+∠D=50°,AB是圓O的直徑,
所以∠AEB=90°,
所以∠BAE=90°-50°=40°.
評析 在與圓的相關證明或者計算問題中,只要碰到“直徑”,都可以嘗試通過構造圓周角的方式來解決問題.構造直角三角形后,將問題轉化到直角三角形中求解,從而實現了問題的等價轉化.
技巧3 圓中有切線,作過切點的半徑
當問題中涉及圓的切線時,需要作過切點的半徑,然后利用半徑和切線之間的垂直關系得到相關等式.同時要注意題目中的一些特殊角,充分利用基本的銳角三角函數定義,而使用三角函數一般都需要在直角三角形內,所以在解題時可嘗試構造直角三角形.
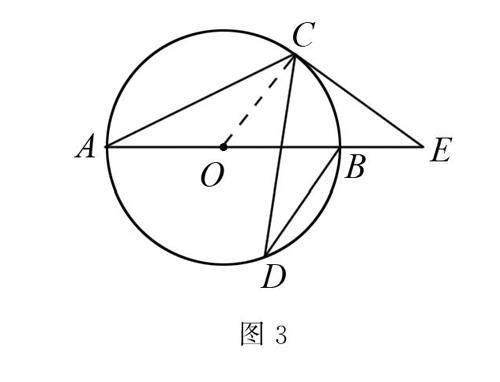
例3 如圖3所示,AB是圓O的直徑,C、D是圓O上的點,∠CDB=20°,過點C作圓O的切線交AB的延長線于點E,則∠E等于()
(A)40°.(B)50°.
(C)60°.(D)70°.
解 連接OC,
因為∠BOC、∠CDB是同弧BC所對的圓心角與圓周角,
所以∠BOC=2∠CDB=2×20°=40°.
因為CE為圓O的切線,
所以OC⊥CE,即∠OCE=90°.
所以∠E=90°-∠BOC=90°-40°=50°.
所以選擇(B)選項.
評析 通過作過切點的半徑的方式,可以建立題目中的已知角度與所求量之間的關系,從而求解出角度的大小.
結語
以上三種技巧是解決與圓有關的問題時常用的作輔助線的技巧.對于綜合性較強的題目,可能需要運用多種方法,但是萬變不離其宗,本質上就是圍繞著圓的定義和圓的性質進行.在平時的解題過程中,要善于思考,善于總結,就能夠得到更多作輔助線的方法.

