2022年版課標中“數量關系”主題的價值意蘊與教學策略

李國強

【摘? ?要】《義務教育數學課程標準（2022年版）》將“數量關系”專設為一個學習主題，有利于培養學生核心素養，提高學生問題解決能力，減輕學生學業負擔。數量關系作為一種心理圖式，其本質是數學模型，源于問題解決，根植于四則運算。為更好地開展“數量關系”主題教學，教師要重視問題基本結構分析，關注學生問題解決思維培養，通過“創設多元化問題情境”“利用直觀圖形”“重視問題基本結構分析”“體驗數量關系建構過程”“全程貫穿、循序漸進”等措施，加深學生對數量關系的理解，實現數量關系學習進階。

【關鍵詞】數量關系；核心素養；教學策略

《義務教育數學課程標準（2022 年版）》（以下簡稱“2022年版課標”）將“數量關系”專設為一個學習主題，凸顯對數量關系的重視。盡管數量關系是貫穿整個義務教育階段的數學內容，但在2022年版課標的“課程內容”中，“數量關系”主題只出現在小學部分。因此，本文討論的內容主要聚焦于小學數學中的數量關系。

針對“數量關系”主題，很多教師存在一些困惑，諸如：何謂數量關系？數量關系的內涵是什么？“數量關系”主題的內容有哪些？學生學習數量關系有何教育價值？數量關系的教學策略有哪些？本文基于2022年版課標中的“數量關系”主題，對上述問題作深入探討，以幫助教師準確把握課標的理念，深入理解數量關系的內涵，從而有效開展“數量關系”主題的教學。

一、2022年版課標中“數量關系”主題的教育價值

數學是研究數量關系和空間形式的科學［1］1，數學的本質表現在數量的關系之中［2］。因此，數量關系在數學中占有重要地位。2022年版課標將原來分散的與問題解決相關的內容進行整合，形成了“數量關系”主題，這有助于教師整體理解和把握以數量關系與問題解決為重點的教學內容，充分發揮數量關系的教育價值。

（一）數量關系是培養學生核心素養的主要載體

2022年版課標立足學生核心素養的發展。從小學階段核心素養主要表現的相關表述中可以看出，數感、符號意識、模型意識、應用意識等都與數量關系密切相關。例如，數感主要是指“對于數與數量、數量關系及運算結果的直觀感悟”，符號意識主要是指“能夠初步運用符號表示數量、關系和一般規律”，模型意識主要是指“對數學模型普適性的初步感悟”，應用意識主要是指“能夠感悟現實生活中蘊含著大量的與數量和圖形有關的問題，可以用數學的方法予以解決”。［1］7-102022年版課標中“數量關系”主題的內容要求、學業要求與教學提示，都指向學生核心素養的培養。［3］

（二）分析數量關系是學生解決問題的關鍵

數學的真諦是問題解決、描述和理解結構與模型。［4］數量關系就像是學生解決問題的思維支架，有助于學生深入分析問題的基本結構和關鍵要素。如果小學數學教學不注重數量關系分析，那么學生就將缺乏對解決問題過程的體驗和對解決問題方法的提煉，這不利于學生形成解題策略、積累解題經驗。因此，分析數量關系是學生順利解決問題的關鍵，培養學生的問題解決能力必須重視數量關系教學。

（三）設立“數量關系”主題有助于減輕學生學業負擔

數學中的基本數量關系是從大量實際問題中抽象與總結出來的，它們深刻揭示了數量之間的內在聯系和規律，為學生解決同類問題提供了思路與策略。理解和掌握這些基本的數量關系有助于學生舉一反三、觸類旁通，進而提高解題的靈活性和效率。在原來的課標中，數量關系被分散在不同的領域，呈現零散化和碎片化的特征，導致數量關系教學被弱化。學生在面對實際問題時，常常因為對數量關系理解不透、解題思路混亂而感到困惑，由此增加了學業負擔。2022年版課標優化了課程內容結構，設立“數量關系”主題，能夠有效強化數量關系教學，提高學生學習效果，減輕學生學業負擔。

二、2022年版課標中“數量關系”主題的內涵意蘊

（一）數量關系的內涵

2022年版課標將數量關系定義為：“主要是用符號（包括數）或含有符號的式子表達數量之間的關系或規律。”［1］18盡管“數量關系”主題屬于小學“數與代數”領域，但它同樣存在于“圖形與幾何”“統計與概率”“綜合與實踐”領域。例如，長方形面積與其長和寬的關系、平均數與樣本數據的關系以及植樹問題中的路長與間隔和棵數的關系等，都屬于數量關系的范疇。為了深入理解數量關系，有必要對其內涵作進一步的認識。

1.數量關系是一種圖式

圖式，作為認知心理學中的一個概念，是指人腦中的一種認知結構。其表征了對某個主題的綜合性知識，反映了某種事物或現象的基本特征和關系。以購物為例，當人們想到購物時，腦海中會浮現超市、貨架、售貨員、顧客、收銀臺等相關信息，并預想自己購物時的情境。從數學角度來看，這種圖式集中體現為購物過程中存在的數量關系，簡化為關系式即付出的錢-購物的錢=找回的錢。［5］

2.數量關系的本質是數學模型

數學是研究模式的科學，而數學模型則是將現實情境用數學語言表達，從數量關系上對現實情境進行的描述與刻畫。數學模型通過去除非本質信息，使數學問題得以簡化。分析實際情境中的數量關系，運用恰當的模型解決問題是數量關系作為學習主題的核心。［6］史寧中教授從數學模型的角度，將小學階段中的數量關系歸納為加法模型和乘法模型兩類，并提出小學數學教學中應重點關注的四個數量關系：總量模型、路程模型、植樹模型和工程模型。

3.數量關系源于問題解決，根植于四則運算

小學數學中的所有數量關系都源于現實生活問題。沒有實際問題，數量關系便失去了存在的意義。實際上，數量關系就是在解決問題的過程中，通過對現象的分析和比較，在把握其本質的基礎上進行抽象和概括得到的。運算的意義是抽象概括數量關系的依據。在小學階段，無論數量關系以何種形式出現，都離不開加、減、乘、除四則運算的意義。簡而言之，小學階段的數量關系主要體現為加減關系、乘除關系以及復合關系。

（二）“數量關系”主題的內容

在2022年版課標中，“數量關系”主題出現在小學部分的“數與代數”領域。這一主題具體涉及哪些內容？這些內容中的數量關系包括哪些類型？這里分別進行梳理與分析。

1.“數量關系”主題的內容要求

研讀2022年版課標中的“課程內容”可以發現，小學數學中的數量關系主要針對生活情境、實際情境等，具體包括以下幾方面內容：（1）用數或字母表示數量之間的關系和變化規律；（2）常見的數量關系，如加法模型、乘法模型等；（3）等式的性質；（4）具體情境或實際問題中的估算；（5）比和比例；（6）利用數量關系解決簡單的實際問題。

2.數量關系分類

從復雜程度來看，小學階段數量關系主要包括簡單數量關系、復合數量關系以及特殊數量關系。簡單數量關系可進一步細分為分合關系和比較關系，其中分合關系涉及部總關系和份總關系，比較關系則包括相差關系和倍數關系。復合數量關系則由上述四種簡單數量關系組合而成。特殊數量關系主要出現在購物、工程和行程等特殊情境之中，如單價×數量=總價、工作效率×工作時間=工作總量、速度×時間=路程等。從模型角度來看，常見的數量關系主要包括加法模型和乘法模型。此外，根據數量關系的表述形式，數量關系可分為直述數量關系和隱含數量關系。［7］直述數量關系是指題目直接呈現數量關系，而隱含數量關系則是題目中未直接給出但學生早已學過的公式或常識性的數量關系，如長方形的面積=長×寬、1時=60分、鴨的腳數=2×只數等。

三、小學數學中“數量關系”主題的教學策略

（一）創設多元化問題情境，為理解數量關系奠定基礎

數學實際問題主要由情境描述與數量關系構成。在日常生活中，學生常常遇到購物類問題，對其有充足的經驗。但對于工程、生產、科技等方面的問題，由于與學生的生活距離較遠，他們理解起來相對困難。解決問題的關鍵在于理解題意，并在已知條件與問題目標之間建立正確的情境表征。存在情境障礙的學生，往往難以準確把握題目中的數量關系。

為培養學生的情境構建能力，教師需要借助多元化的教學手段，如講述故事、閱讀數學繪本、模擬實際活動場景、播放科普視頻等，呈現豐富多樣的問題情境，為學生接觸并理解更廣泛的情境提供有力的支持。學生利用這些間接性經歷，能逐步消除認知的模糊性，理解情境問題的本質，進而增強對數量關系的把握，為提升問題解決能力奠定基礎。隨著學生積累的情境不斷增加，他們將逐漸感悟到各類數量關系的核心要點。例如：合并、增加、移入等都可采用加法運算；減少、剩余、比多、比少等則可采用減法運算；等量組聚集、長方形面積計算、配對問題等都可采用乘法運算；平均分、包含、比分等則都可采用除法運算。

（二）利用直觀圖形，實現數量關系的具象化

小學生的認知水平尚處在從直觀感知到理性理解過渡的階段，他們往往難以準確捕捉數學問題中的數學信息并理解復雜的數量關系。而幾何圖形具有直觀形象的特點，可以讓數量關系的分析更清晰、合理、全面、深入。［8］因此，教師在教學過程中應充分利用幾何圖形的直觀性特點，通過示意圖、列表、線段圖等工具，幫助學生理解數量關系，解決數學問題。

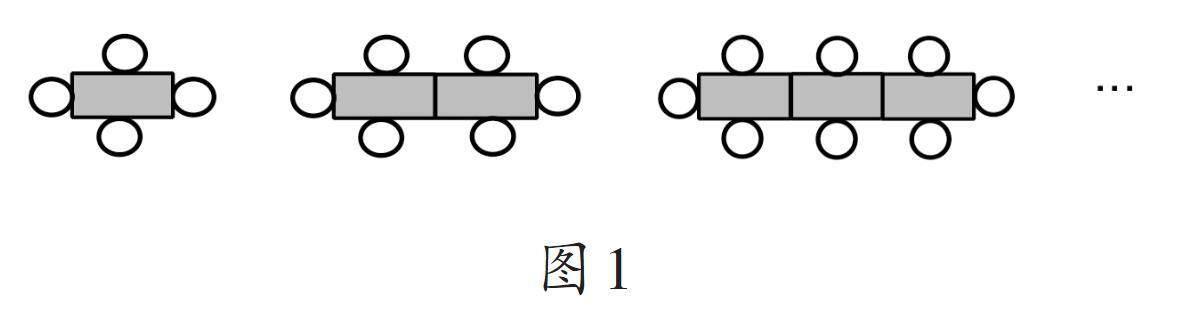
畫示意圖法指的是用“圓圈”“方框”等簡單圖形來代表題目中的事物，以揭示事物之間的數量關系。如“苗族旅游長桌宴”問題：1張桌子可以坐4人，2張桌子可以坐6人，3張桌子可以坐8人。照這樣計算，如果旅游團有40人，需要擺多少張桌子？解決此問題可引導學生畫出示意圖（如圖1）。觀察示意圖不難看出：每增加1張桌子，就多坐2人。進而得出數量關系：總人數=桌數×2+2。

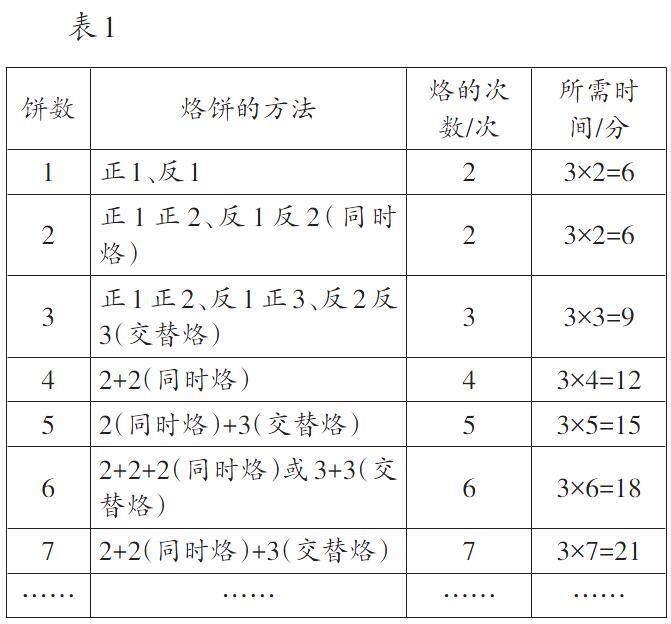
列表法則通過在表格中一一列舉出已知量和未知量及其關系，將復雜的關系清晰化、條理化，便于學生找到其中隱含的數量關系。例如，在“烙餅問題”中，借助列表，可以清晰、直觀地顯示出不同情況下的烙餅方法及餅數、烙的次數和所需時間之間的關系（如表1）。分析歸納后可以發現：烙餅最短時間=3×餅數（餅數≥2）（當餅數=1時，烙餅最短時間=6分鐘）。

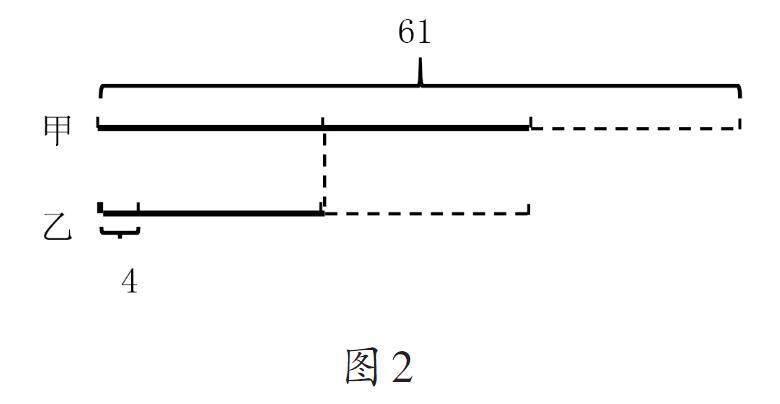
此外，畫線段圖也是解決復合問題的常用方法，尤其在工程問題、行程問題、年齡問題等中更為常見。例如，在“年齡問題”中，甲對乙說：“當我像你這么大歲數時，你剛好4歲。”乙對甲說：“當我長成你這么大歲數時，你就61歲了。”甲、乙今年各是多少歲？通過畫線段圖（如圖2），學生可以清晰、直觀地看出其中的數量關系：4+3×甲乙年齡差=61。據此可以求出甲乙年齡差=19，得到甲、乙年齡分別為42歲和23歲。

總的來說，直觀感知是構建數學模型的關鍵。因此，教師在教學中應根據問題情境和學生的認知特點，選擇合適的直觀圖形，幫助學生理解題意，找到解決問題的突破口，發現數量關系，最終解決問題。

（三）重視問題基本結構分析，加深對數量關系的理解

數學問題由已知條件和問題組成。學生必須厘清題目中條件與條件之間及條件與問題之間的關系，才有可能做出正確解答。為幫助學生更好地理解問題的結構，教師可采用補題、改題、編題等方式，加深學生對數量關系的認識與運用。

1.補題

題目：鳳凰小學二年級有學生165人，___________，五年級有多少學生？請在橫線處補充條件。

本題要求利用已知的二年級學生人數，求出五年級學生人數。增加的條件必須是體現五年級與二年級學生人數關系的語句，如“五年級學生人數比二年級學生人數多33人”“五年級學生人數比二年級學生人數多20%”等。通過補題，學生可以加深對題目中數量之間相互依存關系的理解。

2.改題

題目：王叔叔從縣城出發去王莊送化肥，速度是40千米/時，路上用了3個小時，從縣城到王莊有多遠？

學生完成此題后，教師可將題目改為：王叔叔從縣城出發去王莊送化肥，速度是40千米/時，路上用了3個小時，原路返回用了2小時，返回時平均每小時行多少千米？當然也可以由學生自主改題。改變題目的條件和問題，有助于加深學生對“路程=速度×時間”這一數量關系的理解。

3.編題

教師可以要求學生就某一主題（如購物），按照單價、數量、總價的關系編題。通過這種方式，不僅可以鍛煉學生的數學思維和解題能力，還可以提高他們的信息收集能力和數學語言表達能力。在指導學生編題時，教師應遵循目的性、科學性、教育性的原則，使學生在理解數量關系的同時，形成正確價值觀、必備品格及關鍵能力。

（四）體驗數量關系建構過程，提高解決問題的能力

多數小學生在數學問題解題中出錯，其重要原因往往在于未能建立正確的數量關系，而非計算失誤。［10］復雜的數學問題由若干個基本的數量關系組成，因此，正確構建數量關系成為解決問題的關鍵。

學生在構建數量關系時，通常會經歷“具體事件—情境問題—情境模型—數學模型”這一過程。例如，當學生面對題目“小紅從杭州乘高鐵去北京旅游，用了4.5個小時，高鐵每小時行300千米，杭州到北京有多少千米？”時，他們首先會識別出小紅（不是小明，也不是小剛）乘高鐵這一具體事件。隨后，學生可能會遇到類似的問題：“小剛每天放學騎自行車回家，每分鐘行225米，10分鐘到家，學校離家有多遠？”或“司機叔叔開車送貨，每小時行70千米，4小時行多少千米？”通過對這些問題的分析，學生逐漸從關注具體人物和場景轉向關注更普遍的路程、速度和時間之間的關系。他們將這些情境問題中的共同本質屬性提煉出來，形成如“路程=速度×時間”這樣的情境模型。在此基礎上，與幾個同類的不同情境模型進行對比，如購物問題中的“單價×數量=總價”或工程問題中的“工作效率×工作時間=工程量”等，最終提煉出更為抽象化的數量關系“每份數×份數=總數”，實現數學模型的構建。

通過這樣的抽象概括過程，學生不僅實現了數量關系的結構化遷移和提升，為日后解決同類問題提供了方法和策略，還為學習更為復雜的數學問題奠定了堅實基礎。更重要的是，這種抽象和概括的能力有利于學生打通不同數量關系之間的關系，感到數量關系越學越簡單，從而減輕學生的學業負擔，提高其學習興趣。

（五）全程貫穿、循序漸進，實現數量關系學習進階

小學階段的數量關系主要包括簡單數量關系、復合數量關系以及特殊數量關系。2022年版課標中的“數量關系”主題貫穿三個學段：第一學段主要是運用四則運算意義解決實際問題，第二學段主要學習和運用常見數量關系，第三學段主要學習用字母表示數量之間的關系或規律。

2022年版課標在小學各學段“數量關系”主題的“學業要求”中都給出了明確的學習目標。教師需要根據各學段學生的認知特點，遵循循序漸進的原則，按學段目標實施“數量關系”主題教學。在第一學段，重視四則運算意義，有意識地讓學生體會數量關系。四則運算的意義是運用數量關系解決問題的基礎，是最基本的數量關系模型，對后續學習有深遠影響。第二學段重點關注復合數量關系和特殊數量關系的教學。復合數量關系問題涉及兩個或多個數量關系的綜合應用，因此，需要學生具備分析、思考運算順序和解題策略的能力。而特殊數量關系不僅是對四則運算意義的運用，也是解決更復雜問題的基礎。第三學段需要重點引導學生理解含字母的數量關系，解決較復雜的實際問題。教學中，應引導學生感受字母的一般性，滲透函數思想，培養初步的代數思維。較復雜問題由于涉及不同現實情境，數量關系較為復雜，是整個小學階段數量關系教學的重難點。總而言之，小學階段數量關系的教學是一個由具體到抽象、由感性到理性、由定量到變量的過程。在這一過程中，教師應注重低段的啟蒙、中段的鞏固以及高段的提升，確保學生在整個學習過程中全程參與，循序漸進地實現數量關系學習的進階。

2022年版課標單獨設立“數量關系”主題，凸顯數量關系的教學意義。然而，這并不意味著數量關系應被過分推崇，更不能退回到以前的做法：教師根據數量關系將實際問題細分為多種類型，然后要求學生記憶題型、套用公式，并通過題海戰術，訓練學生的解題速度和所謂的“解題技巧”。這種做法會限制學生的思維能力，加重他們的學業壓力，甚至導致學生厭學。事實上，指向問題解決的教學應將重點聚焦于指導學生認真審題，分析條件與問題之間的內在聯系，引導學生在經歷構建數量關系模型的抽象過程中，提高問題解決能力及思維品質，形成應用意識、模型意識等核心素養。為此，數學教師須準確把握2022年版課標中“數量關系”主題的教育價值，深入理解“數量關系”主題的內涵意蘊，積極探討“數量關系”主題教學的有效策略，真正落實課標理念，切實提高教學質量，促進學生發展和自身專業提升。

參考文獻：

［1］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.

［2］史寧中.基本概念與運算法則：小學數學教學中的核心問題［M］.北京：高等教育出版社，2013.

［3］張丹，王彥偉.核心素養導向下小學數學主題解讀（一）：數量關系［J］.小學數學教師，2023（6）：5-9.

［4］布蘭思福特，布朗，科金，等.人是如何學習的：大腦、心理、經驗及學校（擴展版）［M］.程可拉，孫亞玲，王旭卿，等譯.上海：華東師范大學出版社，2013：146.

［5］巢洪政.數量關系的本質、作用及教學［J］.江蘇教育，2010（1）：30-31.

［6］馬云鵬.怎樣理解“數量關系”學習主題［J］.小學數學教育，2022（11）：11-13.

［7］咼亞慧.小學數學題中三類隱含數量關系提取［D］.武漢：華中師范大學，2017.

［8］蘇賽丹，夏忠.幾何直觀：分析數量關系不可或缺的抓手［J］.教學與管理，2018（8）：33-35.

［9］秦碧芳.如何更好地建立數量關系模型［J］.教學月刊·小學版（數學），2023（10）：30-31.

［10］ANAND P G，ROSS S M. Using computer-assisted instruction to personalize arithmetic materials for elementary school children［J］. Journal of educational psychology，1987，79（1）：72-78.

（杭州師范大學中國教育現代化研究院）