借助單位圓理解三角函數(shù)，發(fā)展數(shù)學(xué)核心素養(yǎng)

賈小宇 劉春艷

摘? 要：?jiǎn)挝粓A在三角函數(shù)內(nèi)容中占有非常重要的地位. 從歷史發(fā)展角度來(lái)看，由關(guān)注具體角的弦值轉(zhuǎn)向任意角的三角函數(shù)，三角函數(shù)與圓的弧長(zhǎng)、弦長(zhǎng)的關(guān)系逐漸清晰化，三角學(xué)的發(fā)展也經(jīng)歷了算術(shù)、代數(shù)、幾何、解析四個(gè)研究階段；三角函數(shù)是周期運(yùn)動(dòng)代數(shù)化的代表，在微積分、幾何等領(lǐng)域具有重要作用. 三角函數(shù)的產(chǎn)生與發(fā)展始終與圓有關(guān)，三角函數(shù)的基本性質(zhì)，是圓的對(duì)稱性的解析表現(xiàn)，教學(xué)中要充分發(fā)揮單位圓的作用. 借助單位圓，從模型角度理解三角函數(shù)概念的數(shù)學(xué)化過(guò)程，從幾何直觀上理解三角函數(shù)的性質(zhì)和誘導(dǎo)公式，從整體上理解三角恒等變換與三角函數(shù)的關(guān)系.

關(guān)鍵詞：三角函數(shù)；單位圓；幾何直觀

中圖分類號(hào)：G633.6? ? ?文獻(xiàn)標(biāo)識(shí)碼：A? ? ?文章編號(hào)：1673-8284（2024）03-0008-06

引用格式：賈小宇，劉春艷. 借助單位圓理解三角函數(shù)，發(fā)展數(shù)學(xué)核心素養(yǎng)［J］. 中國(guó)數(shù)學(xué)教育（高中版），2024（3）：8-13.

三角函數(shù)是一類典型的周期函數(shù)，是高中數(shù)學(xué)函數(shù)主題的重要內(nèi)容.《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）》對(duì)于三角函數(shù)概念和性質(zhì)的內(nèi)容要求中提出：“借助單位圓理解三角函數(shù)（正弦、余弦、正切）的定義，能畫出這些三角函數(shù)的圖象，了解三角函數(shù)的周期性、單調(diào)性、奇偶性、最大（小）值. 借助單位圓的對(duì)稱性，利用定義推導(dǎo)出誘導(dǎo)公式.” 教學(xué)提示中再次強(qiáng)調(diào)：“應(yīng)發(fā)揮單位圓的作用，引導(dǎo)學(xué)生結(jié)合實(shí)際情境，借助單位圓的直觀，探索三角函數(shù)的有關(guān)性質(zhì).” 雖然各版本教材對(duì)于此要求的具體呈現(xiàn)不同，但是單位圓在“三角函數(shù)”一章中始終處于非常重要的位置.

在三角函數(shù)的學(xué)習(xí)中，為什么要借助單位圓？如何借助單位圓？本文從歷史發(fā)展和學(xué)科知識(shí)體系建構(gòu)的角度梳理單位圓與三角函數(shù)的關(guān)系，并從學(xué)科教學(xué)的角度探討如何發(fā)揮單位圓的作用.

一、從歷史發(fā)展角度來(lái)看，三角函數(shù)的產(chǎn)生、發(fā)展與圓緊密聯(lián)系

1. 從研究對(duì)象來(lái)看，由關(guān)注具體角的弦值轉(zhuǎn)向任意角的三角函數(shù)

三角函數(shù)的起源與天文學(xué)聯(lián)系緊密，而圓是天文學(xué)中常用的模型. 古希臘時(shí)期，天文學(xué)家描述天體運(yùn)行理論，如同心球、周轉(zhuǎn)圓或偏心圓模型均利用圓來(lái)刻畫天體運(yùn)行軌道. 這一時(shí)期的代表人物希帕霍斯（Hipparchus，約190BC—125BC）不僅利用周轉(zhuǎn)圓和偏心圓模型解釋了日月運(yùn)動(dòng)，還制作了弦表以完成許多精確測(cè)量. 例如，天體之間距離的計(jì)算依據(jù)天體運(yùn)行軌道形狀、天體相對(duì)地球位移對(duì)應(yīng)的時(shí)長(zhǎng)和角度. 因此，只需要考慮固定角的正弦值便可以完成天體距離的推演. 16世紀(jì)，哥白尼的學(xué)生印度數(shù)學(xué)家利提克斯（G.J.Rhaeticus，1514—1576）將正弦函數(shù)重新定義成直角三角形邊長(zhǎng)的比，從而使平面直角三角學(xué)從球面三角學(xué)中獨(dú)立出來(lái). 在這之后，銳角三角函數(shù)進(jìn)入系統(tǒng)研究階段. 直至三角學(xué)脫離天文學(xué)，數(shù)學(xué)從運(yùn)動(dòng)的研究中引出了一個(gè)基本概念，在之后的二百年里，這個(gè)概念在幾乎所有工作中占中心位置，這就是函數(shù)——或變量間的關(guān)系——的概念. 正弦函數(shù)和余弦函數(shù)是一對(duì)源于圓周運(yùn)動(dòng)、密切配合的周期函數(shù). 因此，銳角三角函數(shù)是通過(guò)研究三角形各種幾何量之間的關(guān)系而發(fā)展起來(lái)的，任意角的三角函數(shù)是通過(guò)研究現(xiàn)實(shí)中的周期現(xiàn)象而發(fā)展起來(lái)的. 1748年，歐拉（Euler，1707—1783）在《無(wú)窮分析引論》中引入角的弧度制，使單位圓上用弧度制表示的角成為三角函數(shù)的自變量.

2. 從研究過(guò)程來(lái)看，三角函數(shù)與圓的弧長(zhǎng)和弦長(zhǎng)的關(guān)系逐漸清晰化

三角函數(shù)的概念經(jīng)歷了漫長(zhǎng)的演化過(guò)程，也經(jīng)歷了與圓從合到分又到合的過(guò)程. 三角函數(shù)首次出現(xiàn)在希帕霍斯的弦表中，表示為在半徑固定的圓中不同弧長(zhǎng)對(duì)應(yīng)的弦長(zhǎng)值. 古印度人發(fā)展了希帕霍斯的思想. 阿耶波多（Aryabhata，約476—550）在《阿耶波多歷數(shù)書》中給出一個(gè)類似的半弦表，說(shuō)明了圓心角的一半與“半弦”的關(guān)系，取半弦（jya或jiva，印度梵文中“弓弦”的意思）定義正弦，現(xiàn)在我們使用正弦函數(shù)“sine”的詞源正是“半弦”. 近十個(gè)世紀(jì)之后，利提克斯發(fā)現(xiàn)了圓心角與弧長(zhǎng)的一一對(duì)應(yīng)關(guān)系，突破傳統(tǒng)正弦函數(shù)弧與弦的對(duì)應(yīng)關(guān)系，將正弦改進(jìn)為角的三角函數(shù)值. 至此，三角函數(shù)在經(jīng)歷了漫長(zhǎng)的依托于圓而存在的時(shí)期后最終脫離了圓. 一個(gè)世紀(jì)之后，歐拉提出三角函數(shù)是對(duì)應(yīng)的函數(shù)線與圓的半徑的比值，從而使三角函數(shù)回歸了圓. 例如，正弦函數(shù)的定義——單位圓上任意弧度角對(duì)應(yīng)的正弦線，在弧度制意義下依然體現(xiàn)的是半弧與半弦的對(duì)應(yīng)關(guān)系.

3. 從研究方法來(lái)看，三角學(xué)經(jīng)歷了算術(shù)、代數(shù)、幾何、解析四個(gè)研究階段

在三角學(xué)萌芽期，三角學(xué)用于報(bào)時(shí)、歷法推算、航海、地理研究等人類實(shí)踐活動(dòng). 它作為一種對(duì)天體運(yùn)行路線和位置觀察推算的方法，慢慢演化為球面三角學(xué)知識(shí). 門內(nèi)勞斯（Menelaus，約70—140）的《球面幾何學(xué)》給出球面三角形的定義及相關(guān)基本概念，比較球面三角形與平面三角形的異同. 例如，球面幾何學(xué)中的大圓相當(dāng)于平面幾何中的直線，小于半圓的大圓圓弧就是其兩端點(diǎn)之間球面上所有路徑中的最短路徑. 又如，三角形是平面幾何研究的核心問(wèn)題，同樣地，球面三角形的研究也是球面幾何學(xué)研究的核心問(wèn)題. 門內(nèi)勞斯借鑒希帕霍斯的成果，用弦長(zhǎng)表示球面三角形邊長(zhǎng)的關(guān)系，進(jìn)行平面三角形定理在球面上的推廣，首次使三角學(xué)脫離天文學(xué). 另外，除了正弦和余弦的計(jì)算，阿拉伯學(xué)者引入正切和余切、正割和余割的概念，從算術(shù)和代數(shù)性質(zhì)上發(fā)展了球面三角學(xué)體系. 在三角學(xué)確立期，三角函數(shù)定義在直角三角形中，目的在于解三角形和進(jìn)行三角計(jì)算，體現(xiàn)在平面三角學(xué)的使用上. 在三角學(xué)成熟期，三角函數(shù)呈現(xiàn)真正意義上的函數(shù)解析性. 牛頓（Isaac Newton，1643—1727）和萊布尼茨（Gottfried Wilhelm Leibniz，1646—1716）給出三角函數(shù)的級(jí)數(shù)展開式. 約翰[?]伯努利（John Bernoulli，1667—1748）和托馬斯·范泰德·拉尼（Thomas Fantet de Lagny，1660—1734）等給出三角函數(shù)的和差公式. 德國(guó)數(shù)學(xué)家邁爾（Frederic-Christian Mayer，1697—1729）在此基礎(chǔ)上推導(dǎo)了解析三角的一般恒等式. 歐拉在《無(wú)窮分析引論》中對(duì)三角學(xué)進(jìn)行了解析的敘述，從基本公式推導(dǎo)出全部公式，并發(fā)現(xiàn)了三角函數(shù)的周期性.

二、從學(xué)科知識(shí)體系來(lái)看，三角函數(shù)的地位和作用也與圓有關(guān)

1. 三角函數(shù)是周期運(yùn)動(dòng)代數(shù)化的代表

由于任意角的三角函數(shù)具有周期性，可以刻畫具有周期變化規(guī)律的運(yùn)動(dòng)，在天文和物理中有大量應(yīng)用. 例如，物理中的單擺是一種簡(jiǎn)諧振動(dòng)，具有固定的頻率、周期和振幅，可以由三角函數(shù)近似計(jì)算單擺運(yùn)動(dòng)的周期. 單擺的問(wèn)題還密切聯(lián)系著地球形狀和萬(wàn)有引力定律的驗(yàn)證，同時(shí)推動(dòng)著牛頓對(duì)二體問(wèn)題和三體問(wèn)題的研究. 又如，歐拉在將三角函數(shù)應(yīng)用于天體運(yùn)動(dòng)的研究中，驗(yàn)證了牛頓在《自然哲學(xué)的數(shù)學(xué)原理》中提出的月球運(yùn)動(dòng)理論，從而引發(fā)了數(shù)學(xué)家們對(duì)三角級(jí)數(shù)的深入研究. 另外，1822年，傅里葉（Baron Jean Baptiste Joseph Fourier，1768—1830）在《熱分析理論》中提出任何函數(shù)不論連續(xù)與否，均可以展開為一系列正弦函數(shù). 這一思想為泛函分析、偏微分方程、計(jì)算數(shù)學(xué)等數(shù)學(xué)領(lǐng)域的發(fā)展提供了數(shù)學(xué)基礎(chǔ).

在物理領(lǐng)域，傅里葉級(jí)數(shù)被廣泛應(yīng)用. 自然界中的大多數(shù)運(yùn)動(dòng)或振動(dòng)表現(xiàn)為周期運(yùn)動(dòng)的疊加，如可見光、琴的和弦等，它們都可以用形如[fx=a0+][n=1∞ancosnπxL+bnsinnπxL]的傅里葉級(jí)數(shù)來(lái)刻畫，其中[L]表示周期.

由此可見，三角函數(shù)在自然科學(xué)和數(shù)學(xué)中的廣泛應(yīng)用使其成為反映現(xiàn)實(shí)世界運(yùn)動(dòng)的一種具有周期變化過(guò)程的重要函數(shù)，也使其成為周期運(yùn)動(dòng)代數(shù)化的代表.

2. 三角函數(shù)在微積分、幾何等領(lǐng)域中的作用

三角函數(shù)是解析幾何學(xué)和周期函數(shù)的分析學(xué)中最為基本和重要的函數(shù).

在微積分中，三角函數(shù)與指數(shù)函數(shù)、對(duì)數(shù)函數(shù)這兩個(gè)基本初等函數(shù)之間存在密切的聯(lián)系. 例如，圓弧下的面積[a2-x2dx]和雙曲線下的積分[x2-a2dx]，兩者相差一個(gè)符號(hào)，前者可以用三角函數(shù)表示，后者與對(duì)數(shù)函數(shù)有關(guān)，由此引發(fā)了三角函數(shù)與對(duì)數(shù)函數(shù)兩者之間關(guān)系的研究，以及對(duì)復(fù)數(shù)的對(duì)數(shù)的討論和歐拉公式特殊形式[eiπ=-1]的發(fā)現(xiàn).

在解析幾何和微分幾何中，借助三角函數(shù)將笛卡兒坐標(biāo)系轉(zhuǎn)換為極坐標(biāo)系，推動(dòng)了平面、空間曲線和曲面的研究工作. 例如，歐拉在《無(wú)窮分析引論》中利用坐標(biāo)變換將一般的三個(gè)變量的二次方程轉(zhuǎn)化成標(biāo)準(zhǔn)型，得到六種曲面. 歐拉在《固體或剛體的運(yùn)動(dòng)理論》中，推導(dǎo)出通常所用的沿一條平面曲線運(yùn)動(dòng)的質(zhì)點(diǎn)的加速度的徑向和法向分量的極坐標(biāo)公式.

在微分方程中，三角函數(shù)可以刻畫特定微分方程的解，從而研究方程所反映的周期現(xiàn)象.

另外，常微分方程理論中的一個(gè)基本問(wèn)題是解的性態(tài)，其中一個(gè)重要問(wèn)題是確定微分方程是否存在周期解. 例如，Massera周期解定理，給出了一維非自制周期系統(tǒng)的周期解存在的條件，建立了解的有界性和周期性之間的聯(lián)系.

借助李群和李代數(shù)的表示，也可以對(duì)微分方程進(jìn)行對(duì)稱性、穩(wěn)定性、周期解等性質(zhì)的分析. 例如，由微分關(guān)系式[xt+][xt=0]控制的簡(jiǎn)諧運(yùn)動(dòng)，通過(guò)定義新的坐標(biāo)[yt=][xt]，將這個(gè)二階方程轉(zhuǎn)化為由兩個(gè)一階方程構(gòu)成的方程組[xy=01-10xy]. 我們可以借助矩陣[01-10]的指數(shù)函數(shù)得到方程組的一個(gè)通解，從而得出結(jié)論[xtyt]是[x0y0]的一個(gè)旋轉(zhuǎn). 由此可知，簡(jiǎn)諧運(yùn)動(dòng)系統(tǒng)的相空間軌道圖是一系列圓心在原點(diǎn)的圓周. 其中，該通解中表示旋轉(zhuǎn)的變換矩陣[costsint-sintcost]是李群SO（2）的群元，相應(yīng)李代數(shù)元為[01-10]，它們反映了相空間軌道的對(duì)稱結(jié)構(gòu).

三、教學(xué)建議

基于前面的分析，我們得出如下結(jié)論.

一是三角函數(shù)產(chǎn)生與發(fā)展的過(guò)程始終與圓有關(guān). 三角函數(shù)的定義是在研究圓的半徑、半弦長(zhǎng)、半弧長(zhǎng)、弦長(zhǎng)、弧長(zhǎng)等量之間對(duì)應(yīng)關(guān)系的基礎(chǔ)上建立起來(lái)的. 之后，三角函數(shù)在微積分、微分幾何、微分方程等數(shù)學(xué)領(lǐng)域中的應(yīng)用也與圓緊密相連，即使是在球面三角學(xué)中，球面的“直線”就是圓，球面三角形由連接球面上三個(gè)頂點(diǎn)的大圓圓弧構(gòu)成，球面三角函數(shù)研究的對(duì)象也與圓有關(guān).

二是與其他基本初等函數(shù)相比，三角函數(shù)最重要的性質(zhì)就是周期性，而圓周運(yùn)動(dòng)是最簡(jiǎn)單也最具代表性的周期運(yùn)動(dòng)模型. 三角函數(shù)逐步發(fā)展為反映現(xiàn)實(shí)世界中具有周期變化過(guò)程的重要函數(shù)，也成為周期運(yùn)動(dòng)現(xiàn)象代數(shù)化的代表.

三是三角函數(shù)與圓都具有很好的對(duì)稱性. 對(duì)稱在數(shù)學(xué)中非常重要. 圓是對(duì)稱性最強(qiáng)的平面圖形，大圓與小圓有相同的對(duì)稱性. 正如畢達(dá)哥拉斯所言：“一切立體圖形中最美的是球，一切平面圖形中最美的是圓……正弦、余弦函數(shù)是一對(duì)用來(lái)描述單位圓的函數(shù). 而圓的本質(zhì)則在于其完美的對(duì)稱性，即其旋轉(zhuǎn)對(duì)稱性和對(duì)于每一個(gè)直徑的反射對(duì)稱性. 所以正弦、余弦函數(shù)的基本性質(zhì)，其實(shí)也就是圓的對(duì)稱性的解析表現(xiàn).”

另外，學(xué)生在初中階段“圖形與幾何”領(lǐng)域已經(jīng)系統(tǒng)地學(xué)習(xí)了圓的相關(guān)內(nèi)容，了解了圓的對(duì)稱性. 因此，在研究三角函數(shù)的概念、性質(zhì)，以及誘導(dǎo)公式、三角恒等變換等內(nèi)容的過(guò)程中，要充分發(fā)揮單位圓的模型作用，借助幾何直觀整體把握三角函數(shù)的內(nèi)容，提升數(shù)學(xué)抽象、數(shù)學(xué)建模等素養(yǎng).

1. 借助單位圓，從模型角度理解三角函數(shù)概念的數(shù)學(xué)化過(guò)程

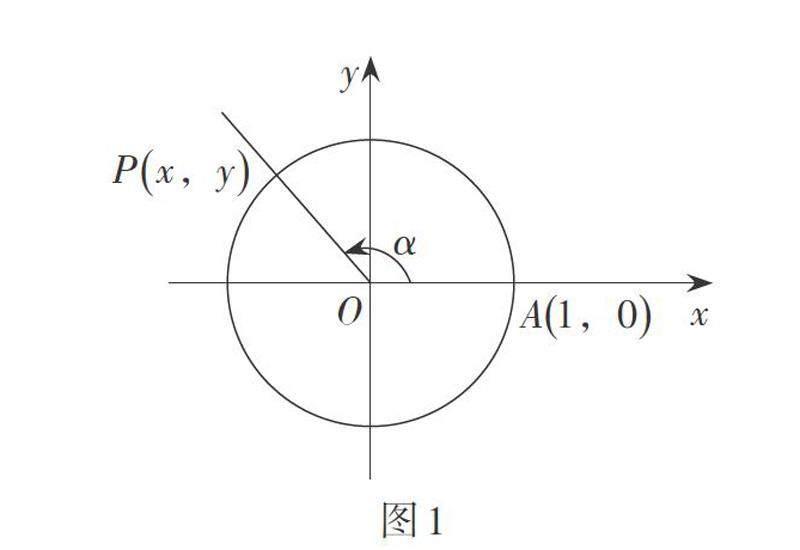
對(duì)于三角函數(shù)的定義，大體有兩種方式：一種是直接借助單位圓，用角的終邊與單位圓交點(diǎn)的坐標(biāo)下定義，稱為單位圓定義法；另一種是沿用銳角三角函數(shù)的定義方法，利用比值下定義，稱為終邊定義法. 兩種方法本質(zhì)上是一致的. 在實(shí)際教學(xué)中，常常從生活中的具體實(shí)例入手. 例如，摩天輪問(wèn)題. 摩天輪勻速旋轉(zhuǎn)過(guò)程中某位游客離地面的高度呈周期性變化，將實(shí)際問(wèn)題抽象成單位圓上點(diǎn)P做勻速圓周運(yùn)動(dòng)，如何刻畫點(diǎn)P的周期性呢？在實(shí)際問(wèn)題中，學(xué)生感受到點(diǎn)P的位置隨時(shí)間[t]的變化而變化，是關(guān)于時(shí)間[t]的函數(shù). 當(dāng)我們把單位圓放在平面直角坐標(biāo)系中研究（如圖1），自然會(huì)想到利用點(diǎn)P的坐標(biāo)刻畫點(diǎn)P的位置，但是選擇哪個(gè)量作為自變量呢？時(shí)間[t]在單位圓的模型中是如何體現(xiàn)的呢？如何建立時(shí)間[t]與點(diǎn)P的坐標(biāo)之間的關(guān)系呢？

前面學(xué)習(xí)其他函數(shù)時(shí)，具體實(shí)例中的自變量和對(duì)應(yīng)關(guān)系是比較容易理解的. 例如，在研究指數(shù)函數(shù)時(shí)，典型的實(shí)例是碳14衰減，此問(wèn)題以時(shí)間作為自變量，能明確寫出兩個(gè)變量之間的解析式. 而對(duì)于三角函數(shù)的概念，需要借助幾何模型，以角作為自變量，建立點(diǎn)的坐標(biāo)與角之間的對(duì)應(yīng)關(guān)系，學(xué)生不具備相關(guān)的學(xué)習(xí)經(jīng)驗(yàn). 因此，對(duì)于三角函數(shù)的概念，如何選擇自變量，以及如何構(gòu)建變量之間的對(duì)應(yīng)關(guān)系是教學(xué)的難點(diǎn).

結(jié)合實(shí)際情境，借助單位圓，我們以時(shí)間[t]作為關(guān)鍵量，研究周期運(yùn)動(dòng)變化. 首先，當(dāng)點(diǎn)P運(yùn)動(dòng)變化時(shí)，觀察單位圓中哪些量也發(fā)生了變化. 當(dāng)點(diǎn)P在單位圓上從點(diǎn)A開始運(yùn)動(dòng)時(shí)，點(diǎn)P旋轉(zhuǎn)的角度與點(diǎn)P經(jīng)過(guò)的弧、弦AP等都發(fā)生了變化. 其次，分析這些變量有什么變化規(guī)律，如何表示. 由于點(diǎn)P做勻速圓周運(yùn)動(dòng)，設(shè)角速度為[ω]，隨著時(shí)間[t]的變化，點(diǎn)P旋轉(zhuǎn)的角度[α=ωt]，點(diǎn)P經(jīng)過(guò)的弧長(zhǎng)l =[αr]. 特別地，在單位圓中，當(dāng)[ω]為單位速度時(shí)，l =[α]= t. 此時(shí)，將問(wèn)題歸結(jié)為對(duì)點(diǎn)P的坐標(biāo)與旋轉(zhuǎn)角[α]之間對(duì)應(yīng)關(guān)系的探索. 接下來(lái)，利用已有的研究函數(shù)的經(jīng)驗(yàn)，借助幾何模型（即單位圓），對(duì)于“幾何元素之間的對(duì)應(yīng)”給出三角函數(shù)的形式化定義.

為此，我們以時(shí)間[t]作為研究的切入點(diǎn)，通過(guò)分析在單位圓上的點(diǎn)的變化過(guò)程中相關(guān)量的變化規(guī)律，借助角速度和線速度的關(guān)系，構(gòu)建旋轉(zhuǎn)角和對(duì)應(yīng)點(diǎn)坐標(biāo)之間的對(duì)應(yīng)關(guān)系，抽象出三角函數(shù)的概念. 通過(guò)上述數(shù)學(xué)化的過(guò)程，達(dá)成以下效果.

（1）幫助學(xué)生進(jìn)一步理解函數(shù)是描述客觀世界中變量關(guān)系和規(guī)律的最為基本的數(shù)學(xué)語(yǔ)言和工具. 在現(xiàn)實(shí)情境中，時(shí)間[t]是常見的變量，通過(guò)經(jīng)歷三角函數(shù)定義的數(shù)學(xué)化過(guò)程，進(jìn)一步體會(huì)如何分析與建構(gòu)其他變量與時(shí)間[t]之間的對(duì)應(yīng)關(guān)系.

（2）幫助學(xué)生理解獲得三角函數(shù)定義與其他基本初等函數(shù)定義的抽象過(guò)程的不同. 前面提到，指數(shù)函數(shù)的定義是通過(guò)對(duì)具體實(shí)例進(jìn)行歸納、概括得到的，實(shí)例中兩個(gè)變量之間具有明確的運(yùn)算關(guān)系，而三角函數(shù)的定義主要是借助幾何模型，通過(guò)分析幾何元素之間的對(duì)應(yīng)關(guān)系得到的.

（3）幫助學(xué)生進(jìn)一步體會(huì)引入弧度制的必要性. 通過(guò)上述過(guò)程，讓學(xué)生直觀感受用弧度制來(lái)度量角，使得三角函數(shù)的研究明顯簡(jiǎn)化.

（4）激活學(xué)生已有的認(rèn)知基礎(chǔ)，幫助他們進(jìn)一步體會(huì)圓的作用，也為后續(xù)利用單位圓研究三角函數(shù)的其他內(nèi)容作好鋪墊.

2. 借助單位圓，從幾何直觀上理解三角函數(shù)的性質(zhì)和誘導(dǎo)公式

性質(zhì)是變化中的不變性和規(guī)律性. 相對(duì)指數(shù)函數(shù)和對(duì)數(shù)函數(shù)，三角函數(shù)的性質(zhì)更加豐富，包括周期性、單調(diào)性、對(duì)稱性、最值等. 三角函數(shù)是借助單位圓，利用幾何要素之間的對(duì)應(yīng)關(guān)系來(lái)定義的，而幾何中圓的對(duì)稱性是學(xué)生的認(rèn)知基礎(chǔ). 因此，借助單位圓的直觀，從運(yùn)動(dòng)變化的角度，利用數(shù)形結(jié)合，更能從整體上理解三角函數(shù)的性質(zhì).

例如，在平面直角坐標(biāo)系xOy中，角[x]的頂點(diǎn)與原點(diǎn)重合，始邊與[x]軸的非負(fù)半軸重合，終邊與單位圓交于點(diǎn)P. 當(dāng)角[x]的終邊繞原點(diǎn)從[x]軸正半軸開始，按照逆時(shí)針?lè)较蛐D(zhuǎn)，觀察運(yùn)動(dòng)變化過(guò)程，并思考以下問(wèn)題.

（1）點(diǎn)P的坐標(biāo)有什么變化規(guī)律？如何用代數(shù)符號(hào)表示？

（2）在角[x]的終邊旋轉(zhuǎn)一周的過(guò)程中，隨著角[x]的變化，點(diǎn)P的坐標(biāo)是如何變化的？利用（1）的結(jié)論，能否給出正弦函數(shù)、余弦函數(shù)的單調(diào)區(qū)間和最值？

（3）圓具有很好的對(duì)稱性，原點(diǎn)O是圓的對(duì)稱中心. 角x和角-x的終邊與單位圓交點(diǎn)的坐標(biāo)有什么關(guān)系？如何用代數(shù)符號(hào)表示？

（4）圓不僅是中心對(duì)稱圖形，也是軸對(duì)稱圖形，[y]軸是單位圓的對(duì)稱軸. 在運(yùn)動(dòng)變化過(guò)程中，存在角[x]的終邊關(guān)于[y]軸對(duì)稱的兩個(gè)位置. 此時(shí)，兩個(gè)位置對(duì)應(yīng)的角的大小有什么關(guān)系？分別對(duì)應(yīng)的正弦值有什么關(guān)系？余弦值呢？如何用代數(shù)符號(hào)表示？

（5）[x]軸也是單位圓的對(duì)稱軸，類比（4）的研究過(guò)程，能得到什么結(jié)論？如何用代數(shù)符號(hào)表示？

（6）直線[y=x]也是單位圓的對(duì)稱軸，能得到什么結(jié)論？

（7）利用圓的對(duì)稱性，還可以研究什么？

每個(gè)基本初等函數(shù)都具有獨(dú)特的性質(zhì)，三角函數(shù)是一類典型的周期函數(shù)，既具有單調(diào)性、奇偶性，又具有非常好的對(duì)稱性. 借助單位圓，通過(guò)觀察圖形，分析運(yùn)動(dòng)變化中的不變性和規(guī)律，用符號(hào)語(yǔ)言表達(dá)，能夠從直觀上理解三角函數(shù)性質(zhì)和誘導(dǎo)公式的本源，體會(huì)數(shù)形結(jié)合方法的作用.

3. 借助單位圓，從整體上理解三角恒等變換與三角函數(shù)的關(guān)系

三角恒等變換是對(duì)三角函數(shù)式進(jìn)行恒等變形. 很多學(xué)生感覺(jué)此內(nèi)容距離三角函數(shù)的概念與性質(zhì)比較遠(yuǎn)，相對(duì)獨(dú)立，又因?yàn)楣蕉嘤洸蛔。杏X(jué)難. 對(duì)于公式的理解，同樣可以發(fā)揮單位圓的作用，幫助學(xué)生建立三角恒等變換與三角函數(shù)的概念、性質(zhì)之間的聯(lián)系，體現(xiàn)三角函數(shù)研究?jī)?nèi)容和研究方法的一致性.

借助單位圓的中心對(duì)稱性，關(guān)于x軸、y軸、直線y = x的軸對(duì)稱得到誘導(dǎo)公式. 對(duì)于圓的任意一條對(duì)稱軸，可以得到什么結(jié)論？不妨以任意角[α]的終邊所在的直線[l]為對(duì)稱軸，在單位圓上任意取一點(diǎn)P. 設(shè)點(diǎn)P關(guān)于直線[l]的對(duì)稱點(diǎn)為點(diǎn)[P′]，角[α]的終邊交單位圓于點(diǎn)A. 連接[PP′]，交直線[l]于點(diǎn)B. 當(dāng)點(diǎn)B在角[α]的終邊OA上時(shí)，如圖2所示；當(dāng)點(diǎn)B在角[α]的終邊OA的反向延長(zhǎng)線上時(shí)，如圖3所示. 如圖2，設(shè)[∠AOP]=[β]，利用三角函數(shù)的定義和對(duì)稱性，得到點(diǎn)[Acosα，sinα]，點(diǎn)[Pcosα+β，sinα+β]，點(diǎn)[P′cosα-β，sinα-β]，點(diǎn)B[cosα+β+cosα-β2， sinα+β+sinα-β2]. 因?yàn)閇OB=OP ? cosβ=cosβ]，由三角函數(shù)的定義得到點(diǎn)[Bcosβcosα，cosβsinα]，所以[cosα+β+cosα-β2=][cosαcosβ]，[sinα+β+sinα-β2=sinαcosβ]. 變形即可以得到和差化積公式和積化和差公式.

另外，圓還具有旋轉(zhuǎn)對(duì)稱性. 以單位圓的圓心為頂點(diǎn)、x軸的非負(fù)半軸為始邊畫出角[α，β，α-β]，根據(jù)三角函數(shù)的定義寫出這三個(gè)角的終邊與單位圓交點(diǎn)的坐標(biāo)，然后利用圓的旋轉(zhuǎn)對(duì)稱性建立等量關(guān)系，再利用兩點(diǎn)間的距離公式得到兩角差的余弦公式. 這樣，以單位圓的幾何直觀為紐帶，將三角恒等變換與整個(gè)三角函數(shù)內(nèi)容融為了一體.

參考文獻(xiàn)：

［1］項(xiàng)武義，張海潮，姚珩. 千古之謎與幾何天文物理兩千年：紀(jì)念開普勒《新天文學(xué)》問(wèn)世四百周年［M］. 北京：高等教育出版社，2010.

［2］克萊因 M. 古今數(shù)學(xué)思想：第一冊(cè)［M］. 張理京，張錦炎，江澤涵，等譯. 上海：上海科學(xué)技術(shù)出版社，2014.

［3］克萊因 M. 古今數(shù)學(xué)思想：第二冊(cè)［M］. 石生明，萬(wàn)偉勛，孫樹本，等譯. 上海：上海科學(xué)技術(shù)出版社，2014.

［4］克萊因 M. 古今數(shù)學(xué)思想：第三冊(cè)［M］. 鄧東皋，張恭慶，譯. 上海：上海科學(xué)技術(shù)出版社，2014.

［5］章建躍. 為什么用單位圓上點(diǎn)的坐標(biāo)定義任意角的三角函數(shù)［J］. 數(shù)學(xué)通報(bào)，2007，46（1）：15-18.

［6］項(xiàng)武義. 基礎(chǔ)幾何學(xué)［M］. 北京：人民教育出版社，2004.

［7］梁宗巨. 世界數(shù)學(xué)通史：上冊(cè)［M］. 沈陽(yáng)：遼寧教育出版社，1995.

［8］VERDUN A. Leonhard Eulers early lunar theories 1725-1752［J］. Archive For History Of Exact Sciences，2013，67（5）：477-551.

［9］MASSERA J L. The existence of periodic solutions of systems of differential equations［J］. Duke Mathematical Journal，1950，17（4）：457-475.

［10］MIWA T，JIMBO M，DATE E. Solitons：Differential equations，symmetries and infinite dimensional algebras［M］. Cambridge：Cambridge University Press，1999.

［11］休森. 數(shù)學(xué)橋：對(duì)高等數(shù)學(xué)的一次觀賞之旅［M］. 鄒建成，楊志輝，劉喜波，等譯. 上海：上海科技教育出版社，2022.

［12］顧沛. 對(duì)稱與群［M］. 北京：高等教育出版社，2011.

［13］項(xiàng)武義. 基礎(chǔ)分析學(xué)之一：?jiǎn)卧⒎e分學(xué)［M］. 北京：人民教育出版社，2004.