“走”出提問誤區(qū)，“問”出課堂精彩

胡軍

[摘 要] 有效的課堂提問需具有明確的目標指向，反映恰當(dāng)?shù)乃季S容量，體現(xiàn)濃郁的學(xué)科特質(zhì)，確保預(yù)設(shè)的動態(tài)生成，從而營造民主和諧的教學(xué)氛圍，提升學(xué)生的學(xué)習(xí)興趣，激活學(xué)生的數(shù)學(xué)思維，激發(fā)學(xué)生主動思考，增進課堂有效性.

[關(guān)鍵詞] 課堂提問；初中數(shù)學(xué)；反思

課堂提問是在教學(xué)過程中，為實現(xiàn)教學(xué)目標，對課堂教學(xué)內(nèi)容設(shè)置問題提問學(xué)生的一種教學(xué)方式. 有效的數(shù)學(xué)課堂提問是激發(fā)學(xué)生在數(shù)學(xué)課堂上積極思維的動力，是開啟學(xué)生智慧之門的鑰匙，是信息輸出與反饋的橋梁，是溝通師生思想認識、產(chǎn)生情感共鳴的紐帶. 然而，目前，初中數(shù)學(xué)教學(xué)中的課堂提問普遍存在“空泛問”“回聲問”“套路問”和“機械問”等通病，這直接影響著數(shù)學(xué)課堂教學(xué)的質(zhì)量生態(tài)，影響著學(xué)生的數(shù)學(xué)思維品質(zhì)培養(yǎng)與素質(zhì)教育實施.

本文主要針對初中數(shù)學(xué)課堂提問中普遍存在的四大通病展開探討，并結(jié)合自己的教學(xué)經(jīng)驗與思考提出改進對策，以便提高初中數(shù)學(xué)課堂教學(xué)的有效性.

通病表現(xiàn)：“空泛問”——問題

籠統(tǒng)化，缺少數(shù)學(xué)問題設(shè)計的

核心關(guān)注

這類提問的具體表現(xiàn)是：問題設(shè)計大而空，目標指向不明確，隨心所欲，缺乏思維導(dǎo)向性，示范借鑒作用較弱. 這種提問產(chǎn)生的主要原因是提問時沒有找準角度，或教師未從系統(tǒng)的角度出發(fā)考慮問題設(shè)置的層級.

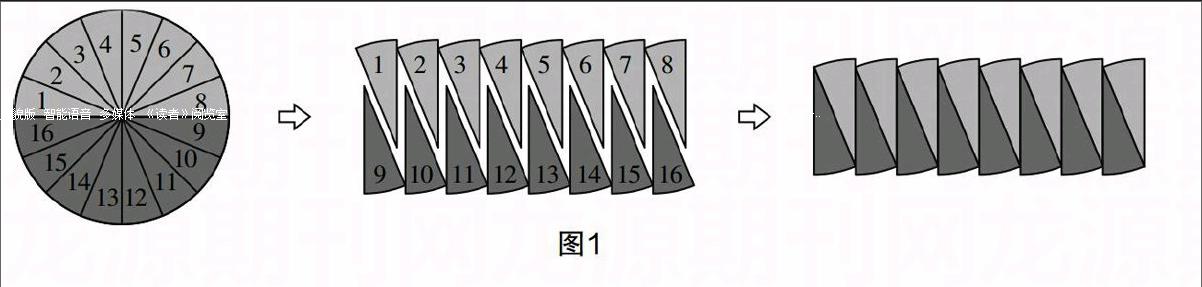
以“圓的面積”教學(xué)為例，某教師先讓學(xué)生分小組動手操作，實現(xiàn)轉(zhuǎn)化，將一個圓平均分成若干份，轉(zhuǎn)化成一個近似的長方形（如圖1）. 教師在“轉(zhuǎn)化”這一環(huán)節(jié)上處理得非常巧妙，通過四次轉(zhuǎn)化（分別把一個圓等分成4份、8份、16份、32份），向?qū)W生滲透極限的思想，接著，教師向?qū)W生提出這樣一個問題：你能推導(dǎo)出圓的面積嗎？

不難看出，該教師提出的這個問題過大、過于空泛，對學(xué)生的引導(dǎo)作用較弱.

對癥處方：數(shù)學(xué)課堂的有效提問——讓問題具有明確的目標指向

數(shù)學(xué)課堂上的課堂提問在設(shè)計問題時要有明確的問題解決指向，即，明確揭示課堂提問的目的所在：或為引入新課，或為教學(xué)前后聯(lián)系，或為突破教學(xué)難點，或為引起學(xué)生爭論，或為總結(jié)歸納等.

在有效的數(shù)學(xué)課堂提問中，強化問題設(shè)計的目標指向性，教師可從兩個方面入手——

一方面，教師要以簡潔明了的語言，讓學(xué)生明確教師提問后的具體任務(wù)，這樣，師生定向思考、聚焦發(fā)力，數(shù)學(xué)課堂就能實現(xiàn)高效. 例如，在“三角形邊的性質(zhì)”教學(xué)中，針對總結(jié)、歸納三角形邊的性質(zhì)，教師不妨設(shè)計這樣的問題：“如果任意給出三條線段，它們一定可以組成一個三角形嗎？”通過此設(shè)問，并組織學(xué)生進行討論及動手操作，便可以幫助學(xué)生理解三角形邊的性質(zhì)，開拓學(xué)生的思路，培養(yǎng)學(xué)生的分析能力和總結(jié)能力. 再回到本文前面提及的“圓的面積”教學(xué)例子上，如果教師在實現(xiàn)圖形轉(zhuǎn)化后，引導(dǎo)學(xué)生觀察、比較、分析，將原問題進一步細化，效果就會不一樣. 比如，教師提出的問題可分割成三個小問題：①圓的面積與拼成的近似的長方形的面積有什么關(guān)系？②拼成的近似的長方形的長相當(dāng)于圓的什么？③拼成的近似的長方形的寬相當(dāng)于圓的什么？改進后的課堂提問呈現(xiàn)了問題鏈式的提問特點，三個小問題由淺入深、由表及里，前一問是后一問的基礎(chǔ)，后一問是前一問的發(fā)展，既有益于大部分學(xué)生對問題的理解，有利于學(xué)生展開思維，又有利于培養(yǎng)學(xué)生分析與解決問題的能力.

另一方面，化大為小，化空泛籠統(tǒng)為具體系統(tǒng). 教師在問題設(shè)計時應(yīng)努力圍繞中心問題，抓住重點，按照先易后難、由淺入深的認識規(guī)律，形成步步深入的遞進系統(tǒng)，課堂提問應(yīng)具有較好的啟發(fā)誘導(dǎo)性、清晰的層次性. 例如，教學(xué)“多邊形的內(nèi)角和”時，教師可設(shè)計下列問題鏈：①三角形的內(nèi)角和是多少度？②你能求出四邊形的內(nèi)角和嗎？③n邊形的內(nèi)角和是否也可以用上面的方法？④你還有其他的方法嗎？這樣，前一個問題是后一個問題的前提，后一個問題是前一個問題的繼續(xù)，每一個問題都是訓(xùn)練學(xué)生思維發(fā)展的一層階梯，從而形成鏈式思考，提高分析、理解的能力. 通過這些問題的引導(dǎo)，明確了“轉(zhuǎn)化”的數(shù)學(xué)思想方法. 再如，在“圓的認識”教學(xué)中，為了引出“圓”的定義，教師可設(shè)計如下系列問題：①車輪是什么形狀？（生答1：圓形）；②是三角形、四邊形，行嗎？（生答2：不行，無法滾動）；③這種形狀（畫橢圓）行嗎？（生答3：不行，會忽高忽低）；④怎樣的圖形才不會忽高忽低？（生答4：輪上的點到軸心等距）. 這樣，教師在課堂提問中就比較自然地引出了學(xué)生對“圓”的定義的正確認識與概括.

通病表現(xiàn)：“回聲問”——問題

淺顯化，缺少數(shù)學(xué)問題思考的

價值內(nèi)涵

“回聲問”多見于學(xué)生或教師解題過程中或結(jié)束后，教師的本來目的是借問題提出（提問）判斷學(xué)生對解題過程、方法和結(jié)論的正確性認識狀態(tài)，含有引導(dǎo)學(xué)生思考其解題過程、方法、結(jié)論是否合理的成分，但由于缺少精致的提問設(shè)計，因此，問題設(shè)計顯得淺顯化，缺少能誘發(fā)學(xué)生進行數(shù)學(xué)問題思考的應(yīng)有價值和內(nèi)涵，該類提問的常見問法有：“對不對”“是不是”等.

例如，在探索“等腰三角形性質(zhì)”的證明過程中，當(dāng)有學(xué)生提出可以作底邊上的高，利用三角形全等證明等腰三角形的兩個底角相等，完成證明后，某教師提問：“作等腰三角形頂角的平分線或底邊的中線，能否也得到兩個全等的三角形呢？”學(xué)生異口同聲：“能！”顯然，該教師如此發(fā)問未能起到充分誘導(dǎo)或引發(fā)學(xué)生思考的作用. 探索等腰三角形性質(zhì)的證明方法，目的是讓學(xué)生發(fā)現(xiàn)常規(guī)輔助線的添加方法，初步提高學(xué)生構(gòu)造全等三角形的能力. 然而，本例中，教師的提問直接告訴了學(xué)生兩種輔助線的作法，只是問學(xué)生“行不行”“能不能”. 這樣的提問，顯得問題膚淺，缺少思維容量，使學(xué)生失去了主動思考“還有哪些輔助線添加方法”的寶貴機會，失去了獨立自主進行創(chuàng)造性思維的空間，最終淪為機械回答教師問題的“回聲筒”.

在日常教學(xué)中，類似的“回聲問”并不鮮見，而其在課堂教學(xué)中的影響無不表現(xiàn)為弊多利少，這主要因為：其一，回答者僅用“是”或“否”就能回答問題，盡管教師也在引導(dǎo)學(xué)生思考，但提問方式本身容易誤導(dǎo)學(xué)生不做思考，思維程度要求很低；其二，這類提問難以發(fā)現(xiàn)學(xué)生的真實水平，“是”或“否”的判斷常包含偶然因素，從概率來說，即使是猜，也有50%的正確率；其三，難以找到學(xué)生的錯誤癥結(jié)，教師一個判斷失誤，可由多種原因?qū)е拢徽业皆蚓蜔o法對癥下藥.endprint

對癥處方：數(shù)學(xué)課堂的有效提問——讓問題具有恰當(dāng)?shù)乃季S容量

從學(xué)生的學(xué)習(xí)認知水平、數(shù)學(xué)學(xué)科的學(xué)習(xí)特點及課堂教學(xué)的有效組織等出發(fā)，數(shù)學(xué)教師在課堂上應(yīng)精心設(shè)計有思考價值的問題. 在問題設(shè)計時，教師不僅要考慮提哪些問題，還要考慮為什么提這些問題，讓每一個問題既為活躍學(xué)生的思維服務(wù)，又成為完成本課教學(xué)任務(wù)的重要組成部分. 譬如，遇到上述需要學(xué)生判斷“是”或“否”的問題時，數(shù)學(xué)教師在該類提問后，可緊跟一些引導(dǎo)敘述算理或引導(dǎo)思考的提問，如“為什么”“有什么不同”“你是怎么想的”等.

為避免“回聲問”在數(shù)學(xué)課堂上不經(jīng)意地出現(xiàn)以及其產(chǎn)生的負面效應(yīng)，數(shù)學(xué)教師對于問題的設(shè)計可從培養(yǎng)學(xué)生的感知能力、綜合分析能力、比較能力、抽象概括能力和創(chuàng)造想象能力等方面入手，從發(fā)展學(xué)生的思維出發(fā)，設(shè)計一些具有一定思考空間、思考價值的問題. 例如，學(xué)生在“平行四邊形面積計算”等知識的學(xué)習(xí)后，三角形面積公式的推導(dǎo)應(yīng)從整體上視為一項重要的學(xué)習(xí)任務(wù). 學(xué)生已經(jīng)體會到在轉(zhuǎn)化的思想下運用“割”“補”的方法推導(dǎo)出平行四邊形的面積公式，在此基礎(chǔ)上，教師可設(shè)計提問：“如何運用推導(dǎo)出平行四邊形面積公式的方法來推導(dǎo)出三角形的面積公式”等，這種較高水平的提問既能突出重點、難點，更能從方法與過程的角度整體掌握知識，從而有效地促進學(xué)生思維的發(fā)展.

通病表現(xiàn)：“套路問”——問題

程式化，缺少數(shù)學(xué)問題解決的

專業(yè)點撥

“套路問”常見于數(shù)學(xué)教師在進行數(shù)式運算、解方程與不等式（組）和幾何論證等知識教學(xué)中. 由于該類數(shù)學(xué)題必須通過大量的、反復(fù)的訓(xùn)練才能達到要求，所以，在課堂教學(xué)中，教師為了讓學(xué)生熟悉這些規(guī)律，不惜不厭其煩地講解、示范，提問往往陷入模式化，難以形成有效的思維力度.

例如，在“一元一次方程的解法”教學(xué)中，不少數(shù)學(xué)教師習(xí)慣于照本宣科，按照“去括號—移項—合并同類項—系數(shù)化為1”的步驟提問，常見的語句有：“下一步該怎樣做呢”等. 學(xué)生在接下來的學(xué)習(xí)活動中，往往是按照教師規(guī)定的程式，“依葫蘆畫瓢”，然而，值得教師反思的是，在許多情況下，學(xué)生并未知其“所以然”，當(dāng)然就更難以有應(yīng)變思維了.

對癥處方：數(shù)學(xué)課堂的有效提問——讓問題具有濃郁的學(xué)科特質(zhì)

數(shù)學(xué)課堂問題要圍繞數(shù)學(xué)課的教育目標，為數(shù)學(xué)學(xué)科的教學(xué)服務(wù)，促進學(xué)生的發(fā)展，萬萬不能漫無邊際，隨意提問. 設(shè)計問題時，要密切創(chuàng)設(shè)數(shù)學(xué)問題與情境的關(guān)系. 數(shù)學(xué)情境的創(chuàng)設(shè)應(yīng)有利于提出的問題設(shè)計，必須處理好問題情境與問題的關(guān)系.

我們再回到前面所述的“一元一次方程的解法”課堂提問中來，如果教師按以下步驟設(shè)計提問：①方程的結(jié)果（解）的形式是怎樣的？②結(jié)果（解）的形式與原方程的形式有哪些差異？③如何消除這些差異？這樣的設(shè)問，在學(xué)生弄清括號、移項等是朝著解的形式轉(zhuǎn)化的目的后，對于解含有分母的方程，也能很清楚地知道第一步是“去分母”. 新的提問既有利于學(xué)生集中注意力，也有利于培養(yǎng)他們的創(chuàng)造性思維，我們便會收到與前面“套路問”截然不同的教學(xué)效果.

再如，在“可能性的大小”課堂教學(xué)中，數(shù)學(xué)教師通常會安排學(xué)生以小組為單位開展下面的游戲：每個小組有一個口袋，裝有若干粉色球和黃色球，教師要求學(xué)生每摸出一個球記錄一次，然后提出問題：一共摸了多少次？其中摸到粉色球多少次？黃色球多少次？教師希望學(xué)生通過動手實踐更好地體會可能性的“大”和“小”，再組織全班匯報，并以各個小組得出的數(shù)據(jù)為依據(jù)，得出結(jié)論：口袋里的粉色球越多，摸到粉色球的可能性就越大；口袋里的黃色球越多，摸到黃色球的可能性就越大. 顯然，教師設(shè)置的“摸球”游戲僅僅產(chǎn)生了學(xué)生在教師指令下機械、重復(fù)地操作，游戲并未真正激發(fā)學(xué)生對“為什么要連續(xù)摸球”這個數(shù)學(xué)問題展開自覺思考. 換句話說，以游戲為載體的課堂提問削弱了學(xué)生在操作過程中對數(shù)學(xué)問題本身的思考. 基于此，改進方案可以是，教師在學(xué)生摸球活動開展前，先告訴學(xué)生，口袋里的球總數(shù)一樣，其中一個口袋粉色球多，另一個口袋黃色球多，接著再提出問題：“能不能不打開口袋，就知道哪個袋里粉色球多？哪個袋里黃色球多”，以此淡化“游戲”成分，突顯學(xué)生對數(shù)學(xué)問題的思考.

■ 通病表現(xiàn)：“機械問”——問題

虛假化，數(shù)學(xué)問題導(dǎo)向缺乏探

究空間

“機械問”只注重問題的結(jié)論，而不追究其得出結(jié)論的過程，或在得到結(jié)論的過程中目的性不明……

例如，在“圓的周長”教學(xué)中，教師為了揭示圓的周長與半徑（直徑）有關(guān)，轉(zhuǎn)動系繩的小球形成一個圓，讓學(xué)生觀察小球運行的軌跡形成的圓的周長，然后縮短繩子的長度，再轉(zhuǎn)動，讓學(xué)生觀察. 教師演示后提問：“圓的周長與什么有關(guān)？”學(xué)生基本上不假思索，齊聲回答：“與半徑有關(guān)”.

上述課堂情景看似師生之間有問有答，其實，這樣的問題回答實際價值并不高. 這是由于，教師在提出問題的同時，實際上已經(jīng)暗示了結(jié)論，提問只是表面的提問，與“注入”沒有質(zhì)的區(qū)別，提問并未使學(xué)生感覺到有進一步思考的必要，所謂的“齊聲回答”其實是屬于機械性的回答. 這樣的提問，表面上看熱鬧活躍，實則流于形式，對啟發(fā)學(xué)生的思維無益.

對癥處方：數(shù)學(xué)課堂的有效提問——讓問題具有通幽的曲徑回旋

在數(shù)學(xué)課堂上，教師要善于提出具有探究趣味的問題，啟發(fā)學(xué)生開展積極的問題思考，而不能使提問顯得直白，以致問題一經(jīng)形成，答案便已告知學(xué)生.

讓數(shù)學(xué)課堂上的教師提問具有通幽的曲徑回旋之美，關(guān)鍵在于教師的課堂提問能夠引發(fā)學(xué)生的探究，能夠便于學(xué)生探究，學(xué)生需經(jīng)過一番“腦筋急轉(zhuǎn)彎”的探究歷程，才能接近和發(fā)現(xiàn)答案，到達勝利的彼岸.

一方面，教師課堂上所提出的數(shù)學(xué)問題應(yīng)具有一定的發(fā)掘價值，面對教師的提問，學(xué)生需在頭腦中經(jīng)過幾番回旋、思考，才能生成正確的結(jié)論. 仍以前面的“圓的周長”教學(xué)為例，教師在提問時注重啟發(fā)，而不是暗示結(jié)果，其效果明顯不一樣. 基于此，教師在課堂提問時不妨另換一種方式，可以讓學(xué)生先猜一猜：“圓的周長與什么有關(guān)？你能想辦法驗證嗎？”事實上，學(xué)生的想法多種多樣，可以是滾動法，也可以是繞繩法. 由于學(xué)生并不能從教師的提問中直接獲得答案，他們需要在動手操作中發(fā)現(xiàn)結(jié)論，因而，他們在操作時便會有明確的目的性，急于探求原因. 這樣的提問與接下來學(xué)生的深入思考以及動手操作緊密聯(lián)系在一起，因此，它們更能引起學(xué)生的探究興趣.endprint

另一方面，教師對提問的設(shè)計應(yīng)與動態(tài)的課堂學(xué)習(xí)緊密聯(lián)系在一起，教師動態(tài)生成問題，誘導(dǎo)學(xué)生動態(tài)探究、趣味學(xué)習(xí)，進而獲得數(shù)學(xué)探究性學(xué)習(xí)旅程中那份特有的曲徑尋幽之樂. 例如，在“特殊四邊形”的探究課教學(xué)時，學(xué)生在探究中點四邊形的過程中所生成的問題偏離了教師的預(yù)設(shè)，教師提出的問題是：“上節(jié)課，我們研究了一般四邊形的中點四邊形是平行四邊形（如圖2），那么，接下來大家說應(yīng)該探討哪些特殊四邊形的中點四邊形呢？”教師原初的預(yù)設(shè)是想讓學(xué)生最好先提出平行四邊形，然后依次把矩形、菱形、正方形和等腰梯形的中點四邊形逐一進行講解，但是，不少同學(xué)都先提出了“梯形的中點四邊形是什么”，這是由于學(xué)生剛學(xué)完“梯形”，見此現(xiàn)狀，教師立刻動態(tài)生成了一個引問：“好！那么我們先從梯形著手，看一下梯形的中點四邊形是哪種特殊四邊形，大家能否根據(jù)上一個例題自己判斷出來呢？”學(xué)生開始動手畫圖探究. 教師預(yù)想學(xué)生會說梯形的中點四邊形是平行四邊形，結(jié)果學(xué)生生成了三種答案：生1認為是平行四邊形（正如教師所愿），生2認為是矩形，生3認為是菱形（其實學(xué)生都是根據(jù)畫圖猜想的）. 此時，教師并沒有馬上做出評判，而是進行追問：“在這三種答案中，你們能夠肯定梯形的中點四邊形一定是什么圖形嗎？為什么？……矩形有可能嗎？菱形有可能嗎？到底是什么決定了中點四邊形的形狀呢？” ……

■

由此可見，教師找準時機引問、追問，并伴隨適時“點撥”，推動問題接近預(yù)設(shè)教學(xué)目標、激活學(xué)生思維非常重要. 因此，在課堂上，教師要善于“有所為”與“有所不為”，當(dāng)面對學(xué)生無法預(yù)知的問題時，可選擇順其自然、因勢利導(dǎo)、尊重生成的“有所不為”，這樣，既可以滿足學(xué)生的求知欲，又能促進課堂教學(xué)資源的生成. 然而，對生成選擇“有所不為”，并不意味著放棄“有所為”，相反，對“有所為”，即教師要在備課時充分預(yù)設(shè)學(xué)生的學(xué)習(xí)活動，推測學(xué)生在活動中可能生成的問題，提出更高的要求. 正是教師對問題設(shè)計、提出、解決的“有所為”與“有所不為”協(xié)奏，才使優(yōu)秀數(shù)學(xué)課堂的締造成為可能.

綜上所述，在初中數(shù)學(xué)課堂教學(xué)中，由于教師的提問通常存在不足，這直接導(dǎo)致課堂教學(xué)提問的效益低下，教學(xué)時常陷入僵局，學(xué)生的數(shù)學(xué)思維品質(zhì)難以有效提升、發(fā)展，因此，為扎實推進數(shù)學(xué)課堂的素質(zhì)教育，數(shù)學(xué)課堂中的有效提問應(yīng)努力從現(xiàn)有問題發(fā)現(xiàn)入手，對癥下藥，有“的”施治，這樣，我們才能讓數(shù)學(xué)課堂妙趣橫生，充分激發(fā)學(xué)生學(xué)習(xí)的積極性，才能使課堂提問有效地促進學(xué)生發(fā)展敏捷和靈活的思維，推進中學(xué)數(shù)學(xué)課堂的教學(xué)改革，推進素質(zhì)教育的深入實施.endprint