如何在平時教學中拿下基礎題

丁偉偉

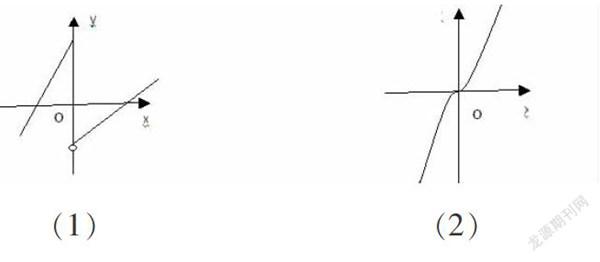
摘 ? ?要： 本文針對江蘇省高考數(shù)學19題（1）問中考生出現(xiàn)的主要問題，談談在平時教學中如何從理解概念和掌握一類問題的基本思路兩個方面真正拿下基礎題.

關鍵詞： 高考數(shù)學 ? ?概念教學 ? ?基本思路 ? ?單調(diào)性

筆者繼2011年高考閱卷后又有幸參加了江蘇省2015年數(shù)學高考閱卷，批閱的正好是19題.第（1）問是含參的三次函數(shù)單調(diào)性討論的基礎題，預測本問得分率應該不低.而實際批改時情況卻很糟糕，最終此問均分不過四點幾分.主要問題有：（1）求完導后無思路;（2）不知道a對進行分類討論;（3）單調(diào)區(qū)間亂放并.針對本小題出現(xiàn)的問題，筆者進行了反思，并結(jié)合平時教學中的措施和體會，談談如何從理解概念和掌握基本思路兩個方面讓學生不功虧于基礎題，以期拋磚引玉.

一、治療區(qū)間亂放并，理解概念是良藥

19題（1）問主要錯誤之一是單調(diào)區(qū)間亂放并.教師在平時教學中對此問題已是苦口婆心，然而盲點依然“逍遙法外”.是學生笨嗎？這個問題真的很難？都不是.是學生沒有真正理解單調(diào)性定義中的“任意”.而“數(shù)學根本上是玩概念的，不是玩技巧.技巧不足道也！”——中國科學院李邦河院士（數(shù)的概念的發(fā)展.《數(shù)學通報》，2009，8）.因此，重視概念教學毋庸置疑.筆者針對單調(diào)性定義的理解作了如下習題教學設計：

例1：畫出下列函數(shù)圖像，并寫出單調(diào)區(qū)間：

（1）y=-x+2; （2）y=（x≠0）

設計意圖：本例來源于課本，旨在反映單調(diào)性是局部性質(zhì)：即函數(shù)在某個區(qū)間上是單調(diào)函數(shù)，但在整個定義域上不一定……