初中數學運用化歸思想解題初探
朱衛星

摘 要: 中學數學知識中蘊含著許多思想方法,就解決問題而言,化歸思想是解決問題的基本思想方法.利用已有知識經驗,化生為熟;應用思維策略,化繁為簡;運用逆向思維,化正為反;借助數學圖形工具,化抽象為具體.通過化歸思想,提高學生綜合應用數學思想的意識與能力.
關鍵詞: 化歸思想 解題能力 初中數學教學
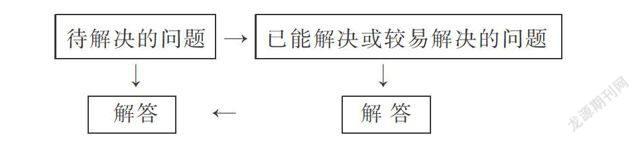
在中學,就解決問題而言,化歸方法是解決問題的基本思想方法.所謂化歸,就是把待解決的問題通過某種轉化過程,歸結到一類已經能解決或者比較容易解決的問題中,借此獲得原問題解決的一種思想方法.在初中生的數學知識體系中,貯藏了一定量的數學公理、性質、定理等基礎知識,通過化歸方法,把所要解決的問題轉化為學生比較熟悉、比較容易的問題,方便求解.化歸的基本模式:
以下是我結合教學過程中的體會,對初中數學運用化歸思想解題的初探.
一、利用已有知識經驗,化生為熟
學習是一個在已有知識經驗體系基礎上不斷積累的過程,后續新知識的學習與解決問題的策略方法,都離不開學生原有的知識體系和數學素養.化歸之“化”,即是將面臨的新問題“轉化”為比較熟悉的問題,在陌生中努力尋找熟悉的因素,以便將問題向著我們熟悉的方向轉化,努力尋找與問題比較接近而又是相對熟悉的問題,化生為熟,運用已知結論或已有解題經驗,使問題得到解決.
例1:蘇科版九年級上冊中,證明圓周角定理:圓周角的度數等于它所對弧上的圓心角度數的一半.
分析:經過操作與思考,學生認識到一條弧所對的圓周角有無數個,這些圓周角對于圓心的位置有3種.如圖,①圓心在圓周角的一邊上;②圓心在圓周角的內部;③圓心在圓周角的外部.對于第一種情形,①圓心在圓周角的一邊上,利用等邊對等角、外角性質,學生能證明其余兩種情形.引導學生自主探索,通過添加輔助線,轉化成第一種情形來證,從而總結出一般規律,圓周角的度數等于它所對弧上的圓心角度數的一半.
解:如圖1,①當圓心在圓周角的一邊上
設∠A=x
∵OA=OB
∴∠OBA=∠OAB=x
∵∠BOC是∠OBA的外角
∴∠BOC=∠OBA+∠OAB=2x
∴∠BAC=∠BOC
如圖2,②當圓心在圓周角的內部:
作直徑AD,轉化成①的情形,圓周角∠BAC=∠BAD+∠CAD;
③當圓心在圓周角的外部:
作直徑AD,轉化成①的情形,圓周角∠BAC=∠BAD-∠CAD.
上述例題中,在學生已解決問題①:當圓心在圓周角的一邊上的前提下,采用迂回的手段將要解決的問題②:圓心在圓周角的內部;③:圓心在圓周角的外部,通過添設輔助線,作直徑AD,變換成熟悉的第一種情形,使問題得以解決.
二、應用思維策略,化繁為簡
當所遇問題結構比較復雜,對于一般學生來講很難直接求解時,我們通常可思考盡可能將問題轉化為比較簡單的易于確定解題方向的問題,從而使新問題得到解決.
∴原方程的解為:-2和1.
通過恰當換元,對問題做形式上的轉換,這樣就容易揭示出問題的內在聯系,化繁為簡,化難為易,使問題輕松獲解,有利于后進生樹立學習信心.
三、運用逆向思維,化正為反
我們在解決問題時,一般從分析題目中的已知條件入手,層層推理,得出所需要求證的結論,有時我們也可以運用逆向思維,化正為反,從與常規思維相反的方向認識問題,從對立的角度思考問題,尋求解題途徑,提高學生分析思維能力和解決復雜問題的能力.
例3:判斷命題“在一個三角形中,至少有兩個銳角,最多有一個鈍角”的真假.
分析:假設三角形中銳角的個數少于2個,那么三角形中就會出現兩個或兩個以上的角是鈍角或直角,兩個鈍角或兩個直角的和加上第三個角的度數一定大于180°,這就違背了三角形內角和是180°的性質,所以一個三角形至少有2個銳角,最多有1個鈍角,從而得出原命題是假命題.
例4:二次函數y=x+bx+c的圖像向左平移三個單位,再向上平移2個單位,得二次函數y=x-2x+1的圖像,求b、c的值.
分析:將二次函數y=x-2x+1的圖像沿著反方向平移,即向右平移3個單位,再向下平移2個單位得到二次函數y=x+bx+c的圖像,就能輕松求出b、c的值.
我們在解決一些問題時,可以運用逆向思維,從問題的對立面入手,化正為反,易于問題的解決.
四、借助數學圖形工具,化抽象為具體
數學學科具有高度的抽象性,為了便于理解問題,平時引導學生根據題意,把涉及的各個數量及數量之間的關系用圖形表示出來,化抽象為具體,增強直觀性,有利于問題的求解.
例5:如圖1,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=2,DE=1,BD=8,設CD=x.
(1)用含x的代數式表示AC+CE的長;
(2)請問點C滿足什么條件時,AC+CE的值最小;
(3)根據(2)中的規律和結論,請求出代數式的最小值.
分析:在解決問題(3)時,我們可以模仿圖1,并由(1)(2)的結果可作BD=12,過點B作AB⊥BD,過點D作ED⊥BD,使AB=2,ED=3,連接AE交BD于點C,如圖2,則AE的長即為代數式的最小值,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質可求得AE的值.借助數學圖形工具,把求形如的代數式的最小值,化為直角三角形,利用勾股定理求解.把“數”的問題,通過“形”使之直觀化,使原問題易于獲得解決.
在列方程解決應用題中,我們常常通過畫線段或畫圖表等方法,將問題直觀化,這樣就容易理解問題中相關數量之間的關系.
例6:某種商品以8元購進,若按每件10元售出,每天可銷售200件,現采用提高售價,減少進貨量的辦法來增加利潤,已知這種商品每漲價0.5元,其銷售量就減少10件.
(1)當售價提高多少元時,每天利潤為700元?
(2)設售價為x元,利潤為y元,請你探究售價為多少元時,利潤最大,最大利潤是多少?分析:設應漲價x元,每天利潤為700元.
在此銷售問題中,涉及漲價前、后的進價、售價、利潤和銷售量,數量較多,引導學生用畫圖表的方法,把這些相關的數量列出來,增強直觀性,方便學生表達漲價后銷售量的代數式,有利于本題的解決.
化歸思想是數學學習中的一種重要思想,是數學解題中普遍使用的方法,平時在教學中引導學生充分審題,仔細觀察,挖掘題意中隱藏的化歸思想方法,充分調動和運用我們已有的知識、經驗和方法,有利于問題的解決,不斷總結應用化歸方法解決問題的規律,提高學生綜合應用數學思想的意識與能力.
參考文獻:
[1]孫高傳.淺談運用化歸思想解題的策略.
[2]曹曉梅.如何在初中數學解題中運用化歸思想.

