試論初中數(shù)學(xué)直覺思維的培養(yǎng)

高慶青

【關(guān)鍵詞】初中數(shù)學(xué) 直覺思維 培養(yǎng)策略

【中圖分類號】G 【文獻(xiàn)標(biāo)識碼】A

【文章編號】0450-9889（2015）10A-0028-01

直覺思維和邏輯思維都在初中數(shù)學(xué)教學(xué)中占有重要地位，一直以來教師對學(xué)生邏輯思維能力的培養(yǎng)都非常重視，但對學(xué)生直覺思維能力的培養(yǎng)不夠，導(dǎo)致學(xué)生思維能力全面、整體的發(fā)展欠缺。筆者經(jīng)過多年探索、實(shí)踐，認(rèn)為在初中數(shù)學(xué)教學(xué)中培養(yǎng)學(xué)生的直覺思維，可以從培養(yǎng)學(xué)生的整體思考、大膽猜想、美學(xué)審視以及數(shù)形結(jié)合這四方面的能力著手。

一、培養(yǎng)學(xué)生整體思考的能力

歸納和猜想，是直覺思維的重要構(gòu)成要素，其水平受整體思考能力的影響。要提高學(xué)生整體思考的能力，就要樹立整體數(shù)學(xué)觀，對數(shù)學(xué)材料的完整結(jié)構(gòu)進(jìn)行全面把握，對問題實(shí)質(zhì)進(jìn)行認(rèn)真理解、消化，對數(shù)學(xué)關(guān)系進(jìn)行細(xì)致概括、總結(jié)，從全局的角度把解題思路確定下來，進(jìn)一步激發(fā)學(xué)生的直覺思維意識，實(shí)現(xiàn)思維創(chuàng)新。

如在教學(xué)人教版七年級數(shù)學(xué)上冊《一元一次方程》時，以方程x-x

-x-9=x-9的求解為例，一般按照“去括號—移項(xiàng)—合并同類項(xiàng)”的常規(guī)思路進(jìn)行求解，但這樣的解題過程比較繁瑣，教師可以探究更為簡便的解題方法。如教師可以引導(dǎo)學(xué)生從整體上認(rèn)真觀察，對方程x-x

-x-9=x-9進(jìn)行詳細(xì)分析，不難發(fā)現(xiàn)方程左邊去中括號后會出現(xiàn)x

-，而方程右邊也有x

-，故可整體合并。合并后可以得出x-x=0，即x=0。實(shí)踐證明，教師要積極培養(yǎng)學(xué)生的整體思考能力，引導(dǎo)學(xué)生在解題過程中透過現(xiàn)象看本質(zhì)，不要僅僅局限于對問題表面的簡單觀察，還要深入內(nèi)部對問題實(shí)質(zhì)進(jìn)行詳細(xì)研究。

二、培養(yǎng)學(xué)生大膽猜想的能力

學(xué)生解決難題時大多會有兩種處理方法：一種是按部就班，立即進(jìn)行計(jì)算、推導(dǎo)；另一種是在計(jì)算、推導(dǎo)前先進(jìn)行初步估測，也就是對問題基本范圍進(jìn)行大膽猜想。因?yàn)楹笳呖梢宰寣W(xué)生更快、更好地解題，因此“大膽猜想”這種教學(xué)手段在初中數(shù)學(xué)教學(xué)中使用甚廣，這就要求教師要有意識地培養(yǎng)學(xué)生大膽猜想的能力，訓(xùn)練學(xué)生不僅要敢于猜想，而且要善于猜想。

如在教學(xué)人教版八年級數(shù)學(xué)上冊《三角形》時，教師可以先引導(dǎo)學(xué)生對多邊形內(nèi)角和進(jìn)行觀察，然后通過提出問題引導(dǎo)學(xué)生思考：一個四邊形減去一角，還剩幾個角？變成什么形狀？學(xué)生進(jìn)行大膽猜想，有3個角的，也有4個角的，還有5個角的，學(xué)生眾說紛紜……之后，教師讓學(xué)生動手實(shí)際操作，學(xué)生就會發(fā)現(xiàn)可以是3個，也可以是4個，還可以是5個。這樣的教學(xué)，讓學(xué)生感受到數(shù)學(xué)的神奇，進(jìn)一步增強(qiáng)他們學(xué)習(xí)數(shù)學(xué)的興趣。因此，教師要積極培養(yǎng)學(xué)生的大膽猜想的能力，引導(dǎo)學(xué)生善于從問題中發(fā)現(xiàn)規(guī)律，進(jìn)而歸納、猜想出結(jié)果，再通過實(shí)際操作來論證自己的猜想。

三、培養(yǎng)學(xué)生美學(xué)審視的能力

簡潔、和諧、對稱等美學(xué)因素一直存在于數(shù)學(xué)領(lǐng)域之中，是引發(fā)數(shù)學(xué)直覺思維的直接動力。教師要善于運(yùn)用數(shù)學(xué)的美學(xué)因素來培養(yǎng)學(xué)生的直覺思維，掌握解題技巧。

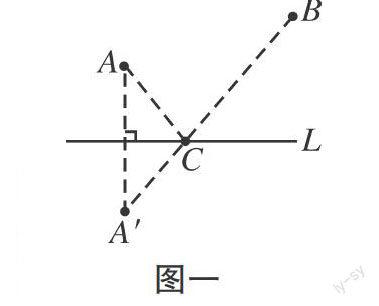
如在教學(xué)人教版八年級數(shù)學(xué)上冊《軸對稱》時，教師可以引導(dǎo)學(xué)生利用軸對稱構(gòu)建數(shù)學(xué)模型，以此來解決生活中的數(shù)學(xué)問題。如：在道路L同側(cè)有兩棟樓A、B（圖一），現(xiàn)要在道路旁建一個公共廁所，要求到A、B的距離之和最短，這個公共廁所應(yīng)建在哪里？教師引導(dǎo)學(xué)生利用軸對稱的知識在直線L上找到唯一點(diǎn)C，使C到A、B兩點(diǎn)的距離之和最小（根據(jù)“兩點(diǎn)間線段最短”），引導(dǎo)學(xué)生建立“軸對稱可解決距離之和最小”的數(shù)學(xué)模型，即“軸對稱數(shù)學(xué)模型”，培養(yǎng)學(xué)生的美學(xué)審視能力。

四、培養(yǎng)學(xué)生數(shù)形結(jié)合的能力

數(shù)與形，是數(shù)學(xué)研究的基本對象，它們之間可以依據(jù)一定條件互相轉(zhuǎn)化，它們之間的這種聯(lián)系稱之為數(shù)形結(jié)合。培養(yǎng)學(xué)生數(shù)形結(jié)合的能力，就是從直覺思維著手，把抽象的數(shù)學(xué)語言、數(shù)量關(guān)系與直觀的幾何圖形、位置關(guān)系結(jié)合起來，從而起到優(yōu)化解題途徑的目的。

如在教學(xué)人教版八年級數(shù)學(xué)下冊《一次函數(shù)》時，教師在講解“函數(shù)的性質(zhì)”時，由于函數(shù)圖象中的點(diǎn)與函數(shù)解析式中的實(shí)數(shù)是相互對應(yīng)的，可以通過引導(dǎo)學(xué)生研究函數(shù)圖象來促進(jìn)其對函數(shù)性質(zhì)的認(rèn)識，實(shí)現(xiàn)直觀與抽象的結(jié)合。可見，通過培養(yǎng)學(xué)生數(shù)形結(jié)合的能力，就能夠把復(fù)雜問題簡單化、抽象問題具體化，可以讓學(xué)生掌握快速有效的解題方法。

總之，教師有意識地培養(yǎng)學(xué)生的直覺思維，可以促進(jìn)學(xué)生創(chuàng)造力、想象力的提升，從而增強(qiáng)學(xué)生直覺思維能力，實(shí)現(xiàn)學(xué)生思維能力的整體、全面發(fā)展。

（責(zé)編 林 劍）