巧借“圖語”策略 豐盈直觀思考力

李銀嵐

【摘要】 數學語言是數學知識的重要組成部分，它既是數學思維的載體，又是數學思維的具體體現(xiàn). 圖形語言具有鮮明的直觀性與形象性，與自然語言與符號語言相互輝映、相得益彰. 在教學中重視并滲透圖形語言，對優(yōu)化小學生數學思維品質，提高直觀思維能力大有裨益.

【關鍵詞】 圖形語言；思維品質；直觀思考力

在數學中，圖形也像文字那樣具有記錄作用，而且比文字更形象、更直觀，有利于人們探索解題途徑和形象記憶，同時又可以交流思想，進行數學思考. 因此，作為語言來使用的圖形，是一種特殊的數學語言即“圖形語言”，簡稱“圖語”.

數學“圖語”是一種視覺語言，通過相關條件畫出圖形，直觀、易懂、明晰，作為文字語言與符號語言的補充，易引起清晰的視覺形象，為抽象的數學概念、原理、定理、法則及數學思維活動和數的計算問題等提供豐富直觀的背景材料，變抽象為具體. 數學“圖語”不只是簡單的文字語言的一種形象表示， 更多的是詮釋其他語言所不能表達的內容. 它包括函數圖像、幾何圖形、圖式、表格、集合的韋氏圖等. 在小學中年級，學生剛從低年級的形象思維階段逐步轉換到具體運算的階段，更需要借助幾何直觀的信息技術手段，培養(yǎng)用“圖語”思考問題的能力.

一、化零為整，勤思畫圖策略

課堂教學上，教師有時需要將一些零散的、個體性的問題看成一個整體來研究，并注意已知條件及問題在這個“整體”中的地位、作用，然后通過畫出相對應的圖形加深對整體結構的理解，并運用轉化使問題獲解，這種對數學問題的整個系統(tǒng)或整個過程進行研究的思維方式稱之為化零為整的思維.

在小學中年級，教師要有意識地培養(yǎng)這種思維，需從直觀教學開始，引導學生勤思畫圖的策略，將直觀圖形與數學語言、符號語言進行合情轉換，在解決數學問題的過程中感悟數與形、形與數之間的轉化，讓幾何直觀能力的培養(yǎng)貫穿在數學學習過程中，以便幫助學生更好地理解數學、學習數學.

首先，教師要借助電子畫板來畫圖理解，通過畫圖使一些題目簡明、直觀，讓學生感受到畫圖解題更加容易理解. 其次，教師要培養(yǎng)學生的畫圖意識，通過純文字做題與轉化成示意圖后解題的比賽，使他們認識到畫圖在解決有關問題時的簡捷實用，從而慢慢習慣并喜歡畫圖. 通過引導學生用數學的語言讀懂圖意，將局部的問題通過適當的增添，使之成為一個整體，讓問題中的局部與整體的關系顯露出來，成為答疑解惑的支點.

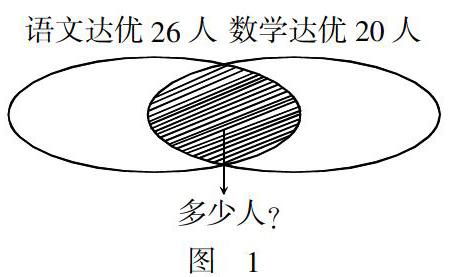
在集合圖中就很容易體現(xiàn)化零為整的數學思想. 例如：三（1）班共有 40 人，在一次檢測中語文達優(yōu)的有26人，數學達優(yōu)的有 20 人，語文、數學都達優(yōu)的有多少人？如果通過電子白板用畫集合圖的方法來理解，問題就迎刃而解了. 如圖1所示.

通過畫集合圖，學生就會發(fā)現(xiàn)圖中重疊部分就表示語文、數學都達優(yōu)的人數，即26 + 20 - 40 = 6（人）.

畫圖固然是一種很重要的解題策略，且方法很多，但在解決實際問題中要靈活應用，應根據需要進行整合，畫出相應的圖來幫助自己分析、理解數量關系，從而解決實際問題.

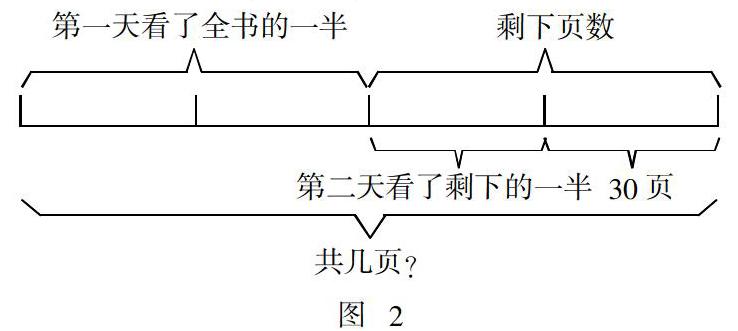
又如，“小東看一本書，第一天看了全書的一半，第二天看了剩下的一半，還剩30頁. 這本書有多少頁？”對于三年級的學生來說，這里的數量關系較為復雜，對兩次“一半”的意義理解是解題的關鍵. 因此，可以借助圖形或線段圖幫助理解：把整本書看成一個整體，第一天、第二天看的頁數可以清晰地在圖上表示出來（如圖2）.

從圖2中可以看出，第二天看的頁數與剩下的30 頁是一樣多的，兩個30頁相加的和又與第一天看的頁數是同樣多的，所以整本書的頁數是：30 × 2 = 60 （頁），60 × 2 = 120（頁）；或者30 × 4 = 120（頁）. 正因為有了直觀圖示的輔助，將零散的一段放在整體圖中思考，使抽象復雜的數量關系變得清晰簡單，便于學生分析與解答.

畫圖是解決問題時經常使用的策略，這個策略能直觀地顯示題意，有條理地表示數量，便于發(fā)現(xiàn)數量之間的關系，從而形成解題的思路. 課堂教學中，教師要根據學生的實際需要、知識經驗、思維發(fā)展水平，讓他們掌握“畫圖策略”的數學技能，逐漸具有應用有效策略的能動性，培養(yǎng)其用圖形語言學習數學知識、理解數學概念的自覺性，形成良好的思維習慣，進而提高學生的思考力、理解力和表達能力.

二、化難為易，慎思析圖策略

數學教學中，經常會碰到條件與條件之間數量關系不是很明確的狀況，有些學生無法直接解題；有時，即使有直觀圖形，學生對圖形的分析能力較弱，也無法順利找出其中的數量關系. 這時就需要通過電子畫板將圖形分解，化難為易，謹慎思考，明晰題意，培養(yǎng)學生的析圖能力，再根據不同的直觀圖進行思考轉換，逐步形成巧妙的解題思路.

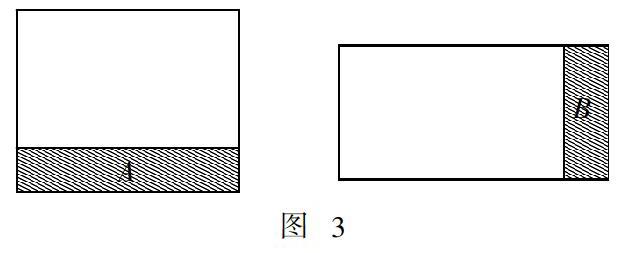
如在講解“一個長方形的周長為 48 米，如果它的寬和長各增加 4 米，面積增加多少平方米？”問題時，可先讓學生分析問題所需的條件及要求，引導學生發(fā)現(xiàn)由長方形的周長是48米這一條件，容易求得長和寬之和為 24米，但題目中未給出長和寬之間的關系，此時有些學生就比較容易卡殼，思路無法展開. 這時，可引導學生分步觀圖，尋找靈感. 如圖3

如果只是寬增加4米，則增加的面積為4與長的積（即為陰影部分A）；如果只是長增加4米，則增加的面積為4與寬的積（即為陰影部分B）；如果長和寬各增加4米，則除了增加面積A和B，還增加了面積C. （如圖4）所以增加的面積為4 × 長 + 4 × 寬 + 4 × 4 = 4 × （長 + 寬 + 4） = 28 × 4 = 112平方米；在討論與交流中，有些學生又經過思考和分析，發(fā)現(xiàn)可以將陰影部分B倒下來移到C的右邊形成一個大的長方形（圖5），只要求出大長方形面積即為增加的面積，而大長方形的長即為長、寬與4的和，寬為4米，所以很快可以求出增加的面積為112平方米.

在此基礎上，要訓練學生的析圖能力，還可以變換題型. 如一個長方形的長增加6米或寬增加4米，面積都增加了48平方米. 求原來長方形的面積？學生在電子畫板上可以清楚直觀地進行割補和分析，從而分別求出長和寬，再求出原長方形的面積.

可見，學生通過謹慎思考，認真分析圖形，將復雜的題型分解成簡單的圖形，然后循序漸進、逐步分析、理出思路，有利于形成用“圖形語言”思考和分析問題的能力.

三、化異為同，廣思串圖策略

如何讓學生在數學學習中自主建構知識，關鍵取決于教師是否創(chuàng)設學生喜聞樂見的認知活動，以學生感興趣的直觀圖形將所學習的基本原理、基本關系凸現(xiàn)出來，通過電子畫板使他們能對串聯(lián)后的圖形中蘊含的基本原理、基本關系進行聚焦性的、反思性的探究，從而在不同中尋找共性，達到研中學，學中悟.

以蘇教版三年級下冊的《認識分數》一課為例：在學生已經初步認識了將一些物體組成的整體平均分成若干份，其中的一份也就是這個整體的幾分之一后，教師依次出示若干幅圖形. 首先出示圖6，問學生陰影部分占整個圓的幾分之幾？學生回答陰影部分占整個圓的，因為整個圓平均分成了5份，而陰影部分占了其中的1份. 接著出示圖7，問學生陰影部分可用幾分之幾表示？學生說也用表示. 師追問，現(xiàn)在是一個完整的圓片，怎么也是呢？學生說因為這里是將5個圓片平均分成5份，陰影部分是其中的1份，所以是這5個圓片的. 為了使同學們對一些物體平均分的理解更深入，老師出示圖8再問陰影部分還可以用表示嗎？學生這時出現(xiàn)兩種答案，一種是認為用表示，因為這里有10個圓片，而陰影部分占了2個；另一種認為還是用表示，因為雖然這里是10個，但還是把它們平均分成了5份，陰影部分占了其中的1份，與里面具體的個數沒關系. 當學生有不同的看法時，教師引導學生分析兩人的判斷：一名同學是看具體分的個數，另一名同學看的是平均分的份數和占的份數. 觀察分數時，到底看什么？讓學生通過電子畫板在不同中尋找共性，通過辨析和比較，認識到分數的本質. 于是教師趁勢在畫板中分別出示芭拉拉魔棒變出的面包圖，如圖9和圖10，讓學生觀察陰影部分可以用幾分之幾來表示，再出示開放題（圖11）讓學生自創(chuàng)分數，來加深對分數本質的理解.

本課教學始終將分數意義的核心“總數量平均分成了幾份——分母， 表示其中的幾份——分子”貫穿于學習的始終， 作為全課的知識“主線”. 無論是從分1個圓片的“舊知”開始， 還是到分5個、10個圓片的跳躍， 最后到48個面包、288個面包的挑戰(zhàn)練習和平均分24個面包的自創(chuàng)分數嘗試， 始終將所有圖形串成一條“主線”展開， 層層推進，環(huán)環(huán)相扣，進行高度聚焦，化異為同，強化對分數意義的直觀理解， 實現(xiàn)了對分數認識的新跨越.

圖形語言是現(xiàn)實生活與數學的絕佳結合點，更是適合小學生年齡特點與心理活動的切入點. 正如我國著名的數學家華羅庚感嘆：“數形本是兩相依，焉能分作兩邊飛. 數缺形時少直觀，形缺數時難入微. 切莫忘，幾何代數統(tǒng)一體，永遠聯(lián)系莫分離. ” “一圖抵萬語”正是華羅庚名言的精確詮釋與實踐過程中的具體操作. 在教學中恰當、及時滲透圖形語言有利于學生理解和掌握數學的基礎知識、基本技能和基本思想，有助于學生順利表達、邏輯思考，會用數學的思考方式解決問題，有利于提高學生直觀思考能力，有利于優(yōu)化學生思維品質. 正如波利亞所說，“畫一張圖，引入適當的符號”. 在解決問題時，可以從已知條件中找到相應的數字特征和代數式的特點、特定的數量關系等，從而充分挖掘幾何意義，引導學生借助電子畫板，通過圖形語言豐盈幾何直觀，從而激發(fā)學習興趣，有效訓練邏輯思考力.

【參考文獻】

[1]何軍. 發(fā)揮圖形語言在數學教學中的作用[J]. 教學與管理，2011（7）.

[2]波利亞. 怎樣解題[M]. 上海：上海科技教育出版社，2007.