教學(xué)“連減的簡(jiǎn)便計(jì)算”磨課有感

王紅妙

[摘 要]連減的簡(jiǎn)便計(jì)算的理論依據(jù)是減法的運(yùn)算性質(zhì)，教師只有引導(dǎo)學(xué)生真正理解減法的運(yùn)算性質(zhì)，在生活實(shí)際中構(gòu)建數(shù)學(xué)模型，總結(jié)出計(jì)算規(guī)律，學(xué)生才能在千變?nèi)f化的題型中做到怎樣簡(jiǎn)便怎樣計(jì)算，從而立于不敗之地。

[關(guān)鍵詞]猜想 驗(yàn)證 理解 轉(zhuǎn)化 應(yīng)用 簡(jiǎn)便計(jì)算 算理

[中圖分類號(hào)] G623.5 [文獻(xiàn)標(biāo)識(shí)碼] A [文章編號(hào)] 1007-9068（2016）23-024

有幸聆聽了特級(jí)教師朱德江《讀懂課堂》的報(bào)告，讓我感觸頗深。為此，我對(duì)“連減的簡(jiǎn)便計(jì)算”的教學(xué)重新思考，在磨課中不斷感悟“我們老師要明白‘教什么‘想教什么‘實(shí)際在教什么‘學(xué)生實(shí)際學(xué)到了什么”，從而打造了高效的數(shù)學(xué)課堂。

案例回放：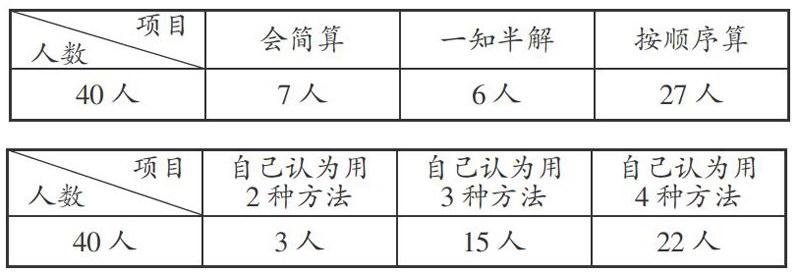

題目：在○里和 上填寫相應(yīng)的運(yùn)算符號(hào)與數(shù)。

（1）868-52-48=868○（52+ ）；

（2）1500-28-272= -（28○272）；

（3）545-167-145= ○ ○ ；

（4）415-74-26= ○（ ○ ）。

交流匯報(bào)到第（3）小題時(shí)，一生回答：“545-167-145=545-167+145。”話音剛落，立即有學(xué)生反對(duì)：“這樣不行。”師隨即加了一個(gè)小括號(hào)，算式變成547-（167+145），追問：“那么，這樣行嗎？”刷地一下，有許多學(xué)生舉起手來，然而一生回答：“這樣也不行！”學(xué)生聽到這樣的回答都把手放下了，師追問：“為什么這樣不行？”這個(gè)學(xué)生理直氣壯地回答：“167+145不能湊成整百數(shù)。”……

思考：

在“連減的簡(jiǎn)便計(jì)算”教學(xué)中，學(xué)生的思維一直停留在“湊成整百就能先相加，再從被減數(shù)里減去，其他的就不行”的層次上，導(dǎo)致出現(xiàn)上述案例中的情況。我突然明白，是我們教師“牽”著學(xué)生去找湊整，為湊整而相加，導(dǎo)致學(xué)生形成547-167-145=547-（167+145）是不對(duì)的一種錯(cuò)誤認(rèn)識(shí)。對(duì)于為什么可以這樣算，學(xué)生沒有真正理解減法的運(yùn)算性質(zhì)，只是知道要這樣算、這樣算簡(jiǎn)便。所以，學(xué)生才會(huì)認(rèn)為把不湊整的兩數(shù)先加起來，再從第一個(gè)數(shù)里減去是不行的，因?yàn)檫@樣計(jì)算不簡(jiǎn)便。

改進(jìn)：

1.了解學(xué)生的認(rèn)知起點(diǎn)

課堂教學(xué)中，教師應(yīng)了解學(xué)生已有的知識(shí)經(jīng)驗(yàn)，把學(xué)生已有的知識(shí)經(jīng)驗(yàn)作為新知識(shí)的生長(zhǎng)點(diǎn)。要想真正了解學(xué)生學(xué)習(xí)的實(shí)際情況，教師不能僅僅靠經(jīng)驗(yàn)，更不能想當(dāng)然，而是需要一定的調(diào)研。為此，我針對(duì)“連減的簡(jiǎn)便計(jì)算”一課教學(xué)設(shè)計(jì)了前測(cè)。如下：

計(jì)算：237-48-52 134-67-34 364-51-64

（選取不同學(xué)習(xí)層次的40個(gè)學(xué)生進(jìn)行前測(cè)，結(jié)果如下表）

我再改變前測(cè)題型，把連減融入問題之中：“王老師有134顆糖，先分給女孩66顆，再分給男孩34顆，現(xiàn)在王老師還剩多少顆糖？”（用不同的方法解決問題）

（依舊選取40個(gè)不同學(xué)習(xí)層次的學(xué)生進(jìn)行前測(cè)，結(jié)果如下表）

40個(gè)學(xué)生全部都能想到66+34=100、134-100=34和134-66-34這兩種方法，只有5個(gè)學(xué)生沒想到用134-34-66這種方法。

通過兩次前測(cè)對(duì)比，發(fā)現(xiàn)學(xué)生在具體情景中基本都能理解并運(yùn)用多種方法解決連減問題，但為什么在純計(jì)算中，學(xué)生不會(huì)用這些方法了呢？這是我們教師應(yīng)該深入思考的問題。其實(shí)，學(xué)生對(duì)減法的運(yùn)算性質(zhì)在頭腦中都有自己的理解，只是沒能用完整的數(shù)學(xué)語言來表述，導(dǎo)致不同方法的算式之間不能順利地進(jìn)行轉(zhuǎn)化。

2.引領(lǐng)學(xué)生理解算理

在前測(cè)中發(fā)現(xiàn)在具體情境下，有將近90﹪的學(xué)生會(huì)用不同的方法解決連減問題。那么，算理應(yīng)如何理解呢？在純計(jì)算中如何根據(jù)數(shù)據(jù)的特點(diǎn)選擇不同形式的轉(zhuǎn)化，達(dá)到簡(jiǎn)算的目的呢？簡(jiǎn)單地說，就是先理解再應(yīng)用，這個(gè)應(yīng)用不是簡(jiǎn)單的記憶模仿，而是在重現(xiàn)知識(shí)形成的過程和理解算理的基礎(chǔ)上。

在新授課中，聯(lián)系具體情境，學(xué)生得出三種計(jì)算方法，并能從計(jì)算結(jié)果相同這一外在形式上的聯(lián)系把連減的三種形式用等號(hào)連接起來，分別比較出左右算式的異同。至此，學(xué)生更多的是停留在對(duì)運(yùn)算規(guī)律外在形式的認(rèn)可上。我認(rèn)為，教學(xué)中應(yīng)讓學(xué)生從生活實(shí)際出發(fā)，引導(dǎo)學(xué)生把重點(diǎn)放在對(duì)問題本質(zhì)的理解上，使學(xué)生能夠真正理解所學(xué)的知識(shí)。只有真正理解減法的運(yùn)算性質(zhì)，才能正確運(yùn)用到連減的簡(jiǎn)便計(jì)算中。如理解“一個(gè)數(shù)連續(xù)減去兩個(gè)數(shù)就等于這個(gè)數(shù)減去后兩個(gè)數(shù)的和”這一性質(zhì)時(shí)，教師可利用數(shù)形結(jié)合的方法，引導(dǎo)學(xué)生從減法意義上理解這兩個(gè)算式為什么相等。同時(shí)，教師可在大屏幕上出示234個(gè)方格，讓學(xué)生借助這些方格說說這兩個(gè)算式為什么會(huì)相等。通過小組交流，學(xué)生很快得出結(jié)論：在234-66-34這個(gè)算式中，234-66是從234個(gè)方格里減去66，再減34是從剩下的方格里面減去34；第二個(gè)算式是先算出一共要減多少個(gè)方格，然后從234里一起減去。這里，第一個(gè)算式是把要減的數(shù)分兩次去減，第二個(gè)算式是把要減的數(shù)加起來后一起減。理解了算理后，學(xué)生對(duì)于a-b-c和a-（b+c）這兩個(gè)算式之間的轉(zhuǎn)化就水到渠成了。

又如，理解“三個(gè)數(shù)連減，可以先減第三個(gè)數(shù)，再減第二個(gè)數(shù)”這一性質(zhì)時(shí)，教師應(yīng)及時(shí)讓學(xué)生列舉現(xiàn)實(shí)生活中的事例，如買東西要付錢的時(shí)候、老師分書本的時(shí)候等。在此基礎(chǔ)上，讓學(xué)生充分舉出一些連減的算式，進(jìn)行形式的轉(zhuǎn)化練習(xí)，辨析不同形式的異同，使學(xué)生由里及表地掌握連減的幾種不同算法。學(xué)會(huì)轉(zhuǎn)化后，教師再引導(dǎo)學(xué)生結(jié)合數(shù)字的特點(diǎn)，進(jìn)行純計(jì)算的簡(jiǎn)便算法練習(xí)。

3.體驗(yàn)感悟所學(xué)知識(shí)

《數(shù)學(xué)課程標(biāo)準(zhǔn)》指出：“數(shù)學(xué)教學(xué)中，要讓學(xué)生親身經(jīng)歷將實(shí)際問題抽象成數(shù)學(xué)模型并進(jìn)行解釋與應(yīng)用的過程。”基礎(chǔ)教育發(fā)生的一個(gè)重大變化，就是教育重心的轉(zhuǎn)移，即把過去單純對(duì)知識(shí)能力的關(guān)注，轉(zhuǎn)向?qū)W(xué)生發(fā)展更全面的關(guān)注。這說明學(xué)生知識(shí)的獲得不是靠教師的傳授，而是在數(shù)學(xué)活動(dòng)中，靠自己去悟、去做、去經(jīng)歷、去體驗(yàn)獲得的。

例如，學(xué)習(xí)加法運(yùn)算定律后緊接著來教學(xué)“連減的簡(jiǎn)便計(jì)算”，這樣是否可以調(diào)動(dòng)學(xué)生已有的學(xué)習(xí)經(jīng)驗(yàn)和方法，通過對(duì)減法運(yùn)算性質(zhì)的猜想進(jìn)行引入？教師教學(xué)中可讓學(xué)生大膽地猜想減法有沒有像加法那樣的運(yùn)算定律，然后讓學(xué)生以小組為單位進(jìn)行自主學(xué)習(xí)，舉例驗(yàn)證減法是否有交換律和結(jié)合律。驗(yàn)證減法是否有交換律時(shí)，經(jīng)過小組討論，有的學(xué)生認(rèn)為沒有，有的學(xué)生舉出三個(gè)數(shù)連減，可以交換后面兩個(gè)減數(shù)的位置的例子。這時(shí)教師可讓學(xué)生加以驗(yàn)證，再舉例。或許會(huì)有學(xué)生寫出35-15-10和15-35-10等算式，教師可引導(dǎo)學(xué)生從中發(fā)現(xiàn)只能交換后面兩個(gè)減數(shù)的位置，第一個(gè)數(shù)的位置不能變，并及時(shí)總結(jié)：“正因?yàn)槿绱耍瑴p法中交換數(shù)的位置是有條件的，和加法的交換律不同，所以我們不叫減法的交換律，而是統(tǒng)稱為減法的運(yùn)算性質(zhì)。”然后繼續(xù)引導(dǎo)學(xué)生利用“猜想——舉例——驗(yàn)證——總結(jié)”的方法，證明第二猜想“一個(gè)數(shù)連續(xù)減去兩個(gè)數(shù)也可以用這個(gè)數(shù)減去后面兩個(gè)減數(shù)的和”。課堂教學(xué)中，教師要始終將學(xué)生推到臺(tái)前，自己充當(dāng)觀眾，并適時(shí)給予引導(dǎo)，使學(xué)生真正理解所學(xué)知識(shí)。

總之，連減的簡(jiǎn)便計(jì)算的理論依據(jù)是減法的運(yùn)算性質(zhì)，教師只有引導(dǎo)學(xué)生真正理解減法的運(yùn)算性質(zhì)，在生活實(shí)際中構(gòu)建數(shù)學(xué)模型，總結(jié)出計(jì)算規(guī)律，才能使學(xué)生在千變?nèi)f化的題型中做到怎樣簡(jiǎn)便怎樣計(jì)算，從而立于不敗之地。

（責(zé)編 杜 華）