淺析小學數學利用線段圖解應用題的方法

姚建忠

摘要：小學數學應用題主要考查學生綜合運用數學知識的能力，是小學數學教學中的重要內容。對于教師來說，如何提高小學數學應用題的教學效果是值得探索的的問題。對于小學生來說，應用題的難度較大。為了幫助教師提高教學效果，使小學生能夠從容應對數學應用題，筆者在文中就如何利用線段圖法解應用題的問題進行分析討論。關鍵詞：小學數學；線段圖；應用題；教學策略

在初次接觸應用題的時候，部分小學生往往會感到很棘手，不知道從哪里入手。這主要是因為部分學生對于基礎概念理解得不透徹，沒有厘清題目中的各項關系，所以無法依據題目中給出的條件進行解答，而運用線段圖可以將抽象的數學概念形象化，幫助學生找出題目中的有價值的信息，從而降低應用題的解答難度。

一、線段圖概述及作用

所謂線段是指位于直線上的兩點之間的最短距離。根據線段圖的定義，我們可以看出，線段圖最明顯的特點就是形象直觀，其次是演示性。因為圖像很容易讓人理解，所以利用線段圖可以直觀地表示數量關系。當需要厘清應用題中的數量關系時，我們可以利用不同長度的線段來表示不同的數量，這其實就是用線段來演示數量，體現了線段圖的演示性。例如小學低年級數學中比較數字的大小問題，如果單純地比較，小學生可能覺得難，但是拿實物來比，學生就很好理解。線段的長短學生們在生活中都經常見到，于是就可以利用線段圖對比大小的問題進行轉換。例如10和7這里兩個數字誰大的問題，可以在一張紙分別畫出10厘米和7厘米的平行線段，線段更長的數字就越大，可知10>7，一目了然。線段圖不單能直觀地展示數字大小，還能幫助學生找出應用題中的隱藏條件，線段圖的主要作用如下：

（一）簡化問題表述

線段圖可以簡化問題表述，尤其是在解決包含比較復雜的數量關系的應用題時。例如這個題目：商店采購了300 公斤大米，第一個月賣掉了180公斤，第二個月賣掉了100公斤，請問還剩多少公斤大米？本來解答這個應用題需要多個步驟，但如果用線段圖來表示這個應用題，解答步驟就變得簡單了。只要引導學生畫一條表示大米總量的線段，然后劃去賣掉的部分，再用總量減去賣掉的部分，答案很容易就知道了。

（二）讓問題更加直觀

小學生對于題目中的語句理解能力不夠，尤其是低年級的學生，這時教師利用線段圖可以將題目的意思直觀地表示出來，例如這個題目：小明有8顆糖，小紅有6顆糖，請問誰的糖更多？多多少？ 在解這道題時，教師可以指導學生畫出線段圖，再根據線段圖來進行講解，引導學生思考，哪條線段表示小明的糖，哪條線段表示小紅的糖，哪條線段更長呢？長出來的那部分是多少呢？學生在教師的引導下來比較兩條線段的長短，問題簡化成了線段的長短。

因為小學生對于抽象概念的理解能力有限，教師在很多時候沒辦法用相關的數學概念讓學生理解清楚數學規律。借助線段圖，引導學生畫線段圖來表示數學概念，可以幫助學生加深對數學概念的理解。此外，在解決數學問題的時候，利用線段圖也能簡化題目，降低解題難度，提高學生們的學習興趣，使學生的動手能力得到提高。

二、線段圖在數學應用題解答中的應用

由上可知，在數學應用題的解答過程中，線段圖的作用很大，下面通過具體例子來分析一下線段圖在數學應用題解答中的應用分類。

（一）線段圖可用來表示總數和份數的關系

總數和份數的關系，主要出現在小學二年級階段，教師在教學中可以借助線段圖來幫助學生系統地理解份數、總數等相關數學概念。

例1：假如有6條小魚，每只小貓2條，可以分給幾只小貓？

教師引導學生用尺子畫出線段圖，并將線段平均分成6等份，告訴學生每等份線段就等于是一條小魚，每只小貓2條，意思就是每只小貓占了2等份的小魚，此時2等份的線段表示一只小貓可以分到的魚，線段總共有6個等份，答案自然是3只，問題得到解決。

（二）借助線段圖表示數字間的倍數關系

在解決數字間的倍數問題時，利用線段圖可以表示得更加清晰，使學生能直觀地感受到倍數關系。

例2：已知紅球的數量是黑球數量的2倍，假如知道黑球的數量為2，問紅球的數量是多少個？

同樣，我們可以用“1”單位長度的一條線段來表示黑球的數量，根據題目條件就可以畫出分別表示黑球和紅球的線段圖。根據線段圖，從而得到以下數量關系

黑球：

紅球：

（1）紅球的數量等于黑球數量乘以2。

（2）黑球的數量等于紅球的數量除以倍數。

（3）紅球的數量除以黑球的數量等于倍數。

因此，這個問題可以衍生出3個不同的問題：

（1）已知黑球的數量和倍數，求紅球的數量。

（2）已知紅球的數量和倍數，求黑球的數量。

（3）已知紅球的數量和黑球的數量，求兩者數量的倍數。

很顯然，借助線段圖不僅可以簡化問題，還能對題目進行擴展，這可以培養學生的發散思維，提高學生的數學綜合能力。

（三）借助線段圖進行數量比較

數量的比較是比較常見的小學數學應用題，其中最最常見的就是數值大小的比較，數量的和與差。我們同樣可以借助線段圖來解決數量比較問題。

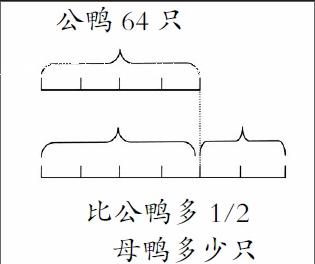
例3：小明的爸爸養鴨子，公鴨總共64只，已知母鴨比公鴨多二分之一，問小明的爸爸總共養了多少只母鴨？

這個題目中的公鴨和母鴨之間的數量關系比較是 比較抽象的，教師可以引導學生利用線段圖來將抽象問題具體化，可以根據題目畫出如下線段圖：

教師引導學生觀察線段圖，學生發現母鴨的數量是在公鴨數量的基礎上加上公鴨數量的二分之一，因此可以得知母鴨的數量=公鴨的數量+公鴨數量的1/2”，從而列出計算式：64+64×1/2。接著，教師再引導學生繼續觀察線段圖，假設公鴨數量的線段長度為1，進一步總結出母鴨的數量=（1+1/2）×公鴨的數量這個規律，當然這里“1/2”是個變量，依據具體的題目改變數字，教師要使學生明白知道確定了線段長度單位“1”，就可以圍繞題目中的信息進行解題。

（四）利用線段圖獲取題目的隱藏信息

教師可以引導學生在解題前比較分析題目，利用線段圖找出題目中隱藏的信息，將文字有效地轉化為圖形語言。

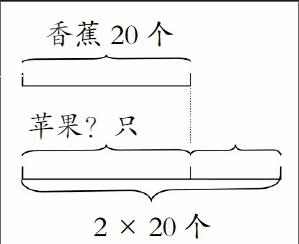
例4：有20根香蕉，已知蘋果的數量是香蕉的2倍，問蘋果比香蕉多多少個？

可以用線段圖將這道題目的信息轉化成圖形：

通過觀察線段圖可知，蘋果的數量是2個20，而香蕉的數量是1個20，因此可以列出計算式：20×（2-1）=20或者20×2-20=20，得出答案。利用線段圖可以找出題目中隱藏條件，蘋果比香蕉多1個20。從而找出數量之間的關系。在引導學生畫線段圖時，教師要鼓勵學生自己思考，培養學生畫線段圖分析題目的良好習慣。

（五）利用線段圖豐富學生的解題思路

在解應用題時，解題思路非常重要，教師應該利用線段圖來引導學生運用發散思維，多角度地分析解決問題，使學生跳出思維定式，形成豐富多樣的解題思路，而不再局限于單一的形式。

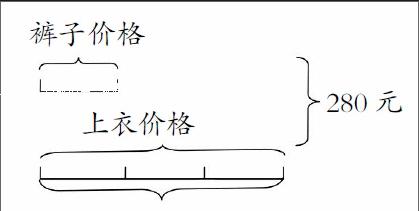
例5：假設一套服裝價格280元，上衣價格是褲子的3倍，問衣服和褲子的價格分別是多少？

教師首先問學生，讓大家想想可以用什么樣的線段來表示這道題目。

學生畫出的線段圖：

教師：大家應該對分數的概念和運算規則都很熟練了，請大家根據線段圖說說這道題的解題思路。

學生1：可以假設褲子的價格為單位“1”，根據上衣與褲子的倍數關系和服裝的總價，得出褲子的價格+3×褲子的價格=280，計算出褲子的價格，然后總價減去褲子的價格就是上衣的價格。

學生2：可以將上衣的價格設為單位“1”，根據題目條件，列出算式：上衣價格+1/3×上衣的價格=280進行計算。

教師：兩位同學回答得很好，其他同學還有新的思路嗎？大家可以結合我們之前學過的列方程知識思考一下。

學生3：可以假設褲子價格為a，根據數量關系列出計算式3a+a=280，這樣計算起來更加方便。

由以上例題可見，在教學中運用線段圖來培養學生的“數形結合”思維，可以讓學生將應用題目中的具體情境轉換成數量與數量之間的關系，數量與問題的關系。

三、結束語

總而言之，運用線段圖來解決小學數學應用題，可以培養學生的數學思維，拓展學生的解題思路，還能鍛煉學生的動手能力。將復雜的數學應用題化繁為簡，使問題迎刃而解。參考文獻：[1]許國華， 楊焱.淺析小學數學利用線段圖解應用題[J].教育界：基礎教育研究， 2014（23）：84-84.[2]張曉華.小學數學利用線段圖解應用題探析[J].中國校外教育：基教版， 2011（12）：48-48.