初中數學數形結合教學要點探究

唐永蓮

摘 要：隨著社會的不斷進步和經濟的快速發展，人們的物質生活水平不斷提高，教育教學也變得越來越重要。初中數學作為一門基礎性學科，數形結合可以把代數問題幾何化，幾何問題代數化，從而幫助初中生更好地學習數學。

關鍵詞：初中數學；數形結合；教學要點

數形結合作為數學研究過程中的一種重要思想方法，在初中數學教學中加以應用，能夠很好地培養學生的創新能力，幫助學生形成數形結合的思維方式，進而為學生的自主學習和發展奠定堅實的基礎。對初中數學數形結合教學要點進行了分析與探討。

一、代數教學中數形結合思想的應用

從初中一年級開始，實數逐漸走進學生的視野，其中以有理數的學習為主體。在有理數的學習中，經常用數軸來表示數，這個過程就已經用到了數形結合思想。可以這樣說，對于每一個實數，在數軸上都有唯一確定的點與之對應。因此，比較兩個實數的大小，就可以通過這兩個數在數軸上對應點的位置關系反映出來。與實數大小比較類似，相反數、絕對值是數軸上的點通過與原點的位置關系定義的。盡管我們教給學生的是（實）數，但不能忽略它的形，也就是與數軸的關系。下面舉一個簡單的例子來說明。

例1.如圖1所示，在數軸上有A，B兩點分別對應實數a，b，下列正確的是（ ）

A.|a|>|b| B.a+b>0 C.ab<0 D.|b|=b

分析：觀察A、B在數軸上的關系，不難得到以下結論，b<0，a>0，且b<-1，a<1，進一步可得，a+b<0，所以B項錯誤；B離原點的距離比A離原點的距離遠，因此|b|>|a|，所以A項錯誤；A、B兩點分別在原點兩側，因此ab<0，所以C項正確；B點在原點左側，絕對值等于其相反數，也就是|b|=-b，所以D項錯誤。故選擇C

選項。

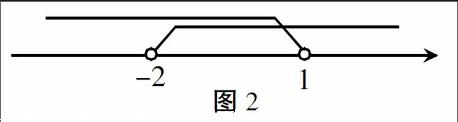
當然，不等式教學也離不開數形結合思想的滲透，比如求解不等式組2（x+2）2x ② ，解不等式①得x<1，解不等式②得x>-2，通過在數軸上分別表示出不等式①、②的解集（如圖2），不難得出原不等式組的解集為-2

二、幾何教學中數形結合思想的應用

在幾何教學中，為了使得所有學生都能學好幾何知識，教師應該給學生滲透數形結合的思想。通過數的精確性以及嚴密性精確表明形的一些屬性，使幾何問題代數化。

例2.如圖3，半圓O上有A，D，G，M四點，四邊形ABOC，DEOF，HMNO均為矩形，設BC=a，EF=b，NH=c，則下列說法哪項是正確的（ ）

A.a>b>c B.a=b=c C.c>a>b D.b>c>a

此題用數的方法難以下手，不妨考慮數形結合的方法，先做出一個半圓，然后分別作出矩形ABOC，DEOF，HMNO，因為BC=OA，EF=OD，NH=OM，而OA，OD，OM都為圓的半徑，所以線段BC=EF=NH，即a=b=c，選擇B選項。

三、概念教學中數形結合思想的應用

要想真正學好數學，就必須徹徹底底吃透數學概念，把握概念核心本質。數學概念是建立數學定理、法則、公式的基礎，同時也是數形結合思想方法的出發點，它反映了事物在數量關系和空間形式方面的本質屬性。初中數學數形結合教學過程中，教師一定要深入分析數學概念，引導學生找出事物之間的共同本質屬性，讓學生通過數形結合相互轉化，體會數學思想和方法。

例如，在講解圓與圓之間的位置關系時，教材上只有文字性的敘述，學生理解起來比較困難，如果引入數形結合思想就可以很好地解決這個問題。設圓心距為d，兩圓的半徑分別為R，r（R>r），那么圓與圓之間的位置關系就可以用圖4明確表現出來。

綜上所述，數形結合思想方法對于學生學好數學起著至關重要的作用，初中數學教師應該結合學生實際生活情況，潛移默化地給學生滲透數形結合的思想方法，讓學生在解決實際問題時能夠有效應用數形結合思想方法，養成良好的學習習慣，從而有效提升學生的數學學習能力。

參考文獻：

[1]肖前英，劉志杰.數形結合思想在初中數學教學中的滲透探究[J].教育，2015（42）：27.

[2]章南海.“數形結合”思想在初中數學教學中的滲透探究[J].讀寫算（素質教育論壇），2014（21）：43-44.

編輯 趙飛飛