基于MATLAB和學科競賽構建高等數學研究性教學課堂

曹玉松+邱穎豫+鄢靖豐

摘 要：文章分析了MATLAB和學科競賽的特點。以研究性教學為目標，以學科競賽為依托，將MATLAB和學科競賽引入到高等數學課堂，從而構建高等數學的研究性教學課堂，為高等數學的研究性教學提供了參考建議。

關鍵詞：學科競賽；研究教學；教學改革；高等數學

一、 概述

高等數學是理工科各專業的基礎課，它所提供的數學思想、數學方法是理工科各專業學生學習其后續課程的基礎，但是傳統的教學方法重理論，輕應用，使得學生對高等數學的應用能力不強，從而不能很好地為專業課服務，為學科競賽服務。高等數學自身具有理論嚴謹抽象，內容繁雜的特點，傳統的教學模式重理論，輕應用，使得學生對涉及的部分理論知識沒有一個直觀的認識，相應地會產生危難情緒，久而久之學習興趣下降，因此有必要對現有的高等數學教學模式進行改革。

MATLAB具有強大的數值計算功能，可以方便地處理矩陣計算，進行圖形繪制，符號運算，程序設計，仿真應用，將MATLAB引入到高等數學教學中，可以有效地激發學生的學習興趣和動手能力，是一種具有實踐意義的教學方法。

近年來，學科競賽在各大高校開展得轟轟烈烈，學科競賽是培養大學生創新實踐能力和動手能力的重要途徑，通過學科競賽可以鍛煉學生的動手能力，學生的團隊合作意識，學科競賽的重要載體就是研究性教學模式的構建。

基于MATLAB 和學科競賽的以上特點，我們可以把學科競賽和MATLAB引入高等數學課堂教學中，構建高等數學的研究性課堂，把傳統的僅靠板書的課堂改為與計算機相結合，提高學生學習高等數學的興趣，本文從下面幾個方面說明如何將MATLAB和學科競賽相關內容引入到高等數學課堂構建研究性教學模式。

二、 將MATLAB引入到高等數學課堂構建研究性課堂案例

理工科的學科競賽會大量應用到高等數學的相關知識，各類模型的構建都離不開高等數學知識，若直接利用高等數學解決相關問題會帶來許多不便，MATLAB提供的數值運算、圖像繪制、程序設計和系統仿真等功能，可以利用簡單的命令函數命令實現，可以將使用者從繁瑣的運算中解放出來，方便快捷地實現相關問題的求解。

（一） 利用MATLAB擬合曲線

根據輸入數據X和Y生成一個N階的擬合多項式。D=polyval（p，x），根據數據X，用擬合多項式p生成擬合好的數據。

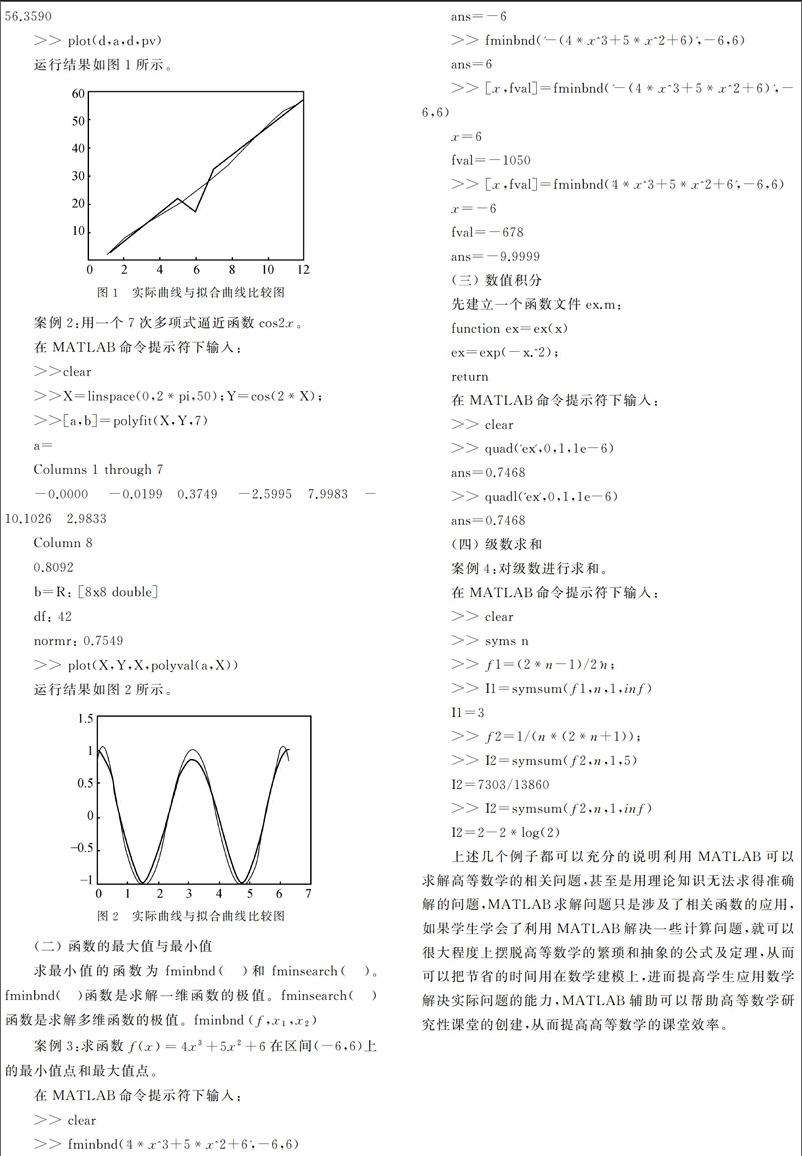
案例1：下面這組數據為檢測儀器采樣結果：2，7，12，17，22，17，32，37，42，47，52，57，求這組數據的擬合方程。

方法：在MATLAB命令提示符下輸入：

>> clear

>> d=1：12；

>> a=[2 7 12 17 22 17 32 37 42 47 52 57]；

>> p=polyfit（d，a，4）；

>> px=poly2str（p，x'）；

>> pv=polyval（p，d）；

>> p，pv

p=-0.0102 0.2561 -2.0158 10.1771 -6.5354

pv=

Columns 1 through 6

1. 8718 7.6410 11.9417 15.6985 19.5913 24.0552

Columns 7 through 12

29.2805 35.2129 41.5532 47.7576 53.0373 56.3590

>> plot（d，a，d，pv）

運行結果如圖1所示。

案例2：用一個7次多項式逼近函數cos2x。

在MATLAB命令提示符下輸入：

>>clear

>>X=linspace（0，2*pi，50）；Y=cos（2*X）；

>>[a，b]=polyfit（X，Y，7）

a=

Columns 1 through 7

-0.0000 -0.0199 0.3749 -2.5995 7.9983 -10.1026 2.9833

Column 8

0.8092

b=R：[8x8 double]

df：42

normr：0.7549

>> plot（X，Y，X，polyval（a，X））

運行結果如圖2所示。

（二） 函數的最大值與最小值

求最小值的函數為fminbnd（ ）和fminsearch（ ）。fminbnd（ ）函數是求解一維函數的極值。fminsearch（ ）函數是求解多維函數的極值。fminbnd（f，x1，x2）

案例3：求函數f（x）=4x3+5x2+6在區間（-6，6）上的最小值點和最大值點。

在MATLAB命令提示符下輸入：

>> clear

>> fminbnd（'4*x^3+5*x^2+6'，-6，6）

ans=-6

>> fminbnd（'-（4*x^3+5*x^2+6）'，-6，6）

ans=6

>> [x，fval]=fminbnd（'-（4*x^3+5*x^2+6）'，-6，6）

x=6

fval=-1050

>> [x，fval]=fminbnd（'4*x^3+5*x^2+6'，-6，6）

x=-6

fval=-678

ans=-9.9999endprint

（三） 數值積分

先建立一個函數文件ex.m：

function ex=ex（x）

ex=exp（-x.^2）；

return

在MATLAB命令提示符下輸入：

>> clear

>> quad（'ex'，0，1，1e-6）

ans=0.7468

>> quadl（'ex'，0，1，1e-6）

ans=0.7468

（四） 級數求和

案例4：對級數進行求和。

在MATLAB命令提示符下輸入：

>> clear

>> syms n

>> f1=（2*n-1）/2^n；

>> I1=symsum（f1，n，1，inf）

I1=3

>> f2=1/（n*（2*n+1））；

>> I2=symsum（f2，n，1，5）

I2=7303/13860

>> I2=symsum（f2，n，1，inf）

I2=2-2*log（2）

上述幾個例子都可以充分的說明利用MATLAB可以求解高等數學的相關問題，甚至是用理論知識無法求得準確解的問題，MATLAB求解問題只是涉及了相關函數的應用，如果學生學會了利用MATLAB解決一些計算問題，就可以很大程度上擺脫高等數學的繁瑣和抽象的公式及定理，從而可以把節省的時間用在數學建模上，進而提高學生應用數學解決實際問題的能力，MATLAB輔助可以幫助高等數學研究性課堂的創建，從而提高高等數學的課堂效率。

三、 將MATLAB引入到學科競賽

學科競賽是在課堂教學的基礎之上，考查學生利用所學的基礎知識和專業知識解決實際問題的能力。當前，越來越多的學校都花費了大量的人力物力投入到學科競賽中，學科競賽對學習的促進效果已經顯現出來，開展學科競賽可以培養學生的動手能力和團隊協作能力，提高理工科學生的工程能力，學科競賽的成績已成為衡量教學水平和教學質量的重要指標。但在學科競賽中常常會面臨一些無法用理論求得精確解的問題，但是MATLAB提供的強大的計算功能卻可以給出其數值解，從而解決學科競賽中的實際問題，另外，即使對于一些可以用理論知識求解的問題，利用MATLAB也可以大大地節約運算時間，因此MATLAB引入到學科競賽解決相應的數學模型具有較強的現實意義，這就要求在高等數學課堂上需要將MATLAB和學科競賽相結合，利用案例教學，構建高等數學的研究性教學課堂。

四、 結束語

基于MATLAB和學科競賽構建高等數學研究性教學課堂，旨在將MATLAB和學科競賽中的部分案例教學引入到高等數學課堂教學中去，MATLAB強大的數值計算功能大大增加了高等數學的實用性，弱化了高等數學的抽象程度，學科競賽案例的引入可以使得高等數學與專業問題結合起來，提高學生分析問題、解決問題的能力。

參考文獻：

[1] 林海濤.MATLAB在《高等數學》教學中的輔助功效研究 [J].開封教育學院學報，2016，36（5）：133-134.

[2] 李小梅，葉賽英.重探究、重應用、重體驗——研究性學習法的具體舉例——以高等數學課程為例.數學教學研究，2014，33（2）：45-49.

[3] 徐永梅.高等數學實施探究性教學模式教學效果評價模型分析.價值工程，2016， 35（16）：188-190.

[4] 陳瑩，肖依，趙中.高等數學研究性學習教學法.洛陽師范學院學報，2015（2）：124-126.

[5] 湯永龍，黃錦，唐云華.高等數學教學改革之研究.課程教育研究，2014（30）：54-55.

[6] 曹玉松，邱穎豫.基于學科競賽的高等數學研究性教學的構建.吉林省教育學院學報，2016，32（6）：75-77.endprint