芻議初中數學“問題解決”

沈春梅

[摘? 要] 在核心素養培育的背景下，對問題解決的理解需要緊扣“問題”“問題解決”等幾個核心概念來進行. 其中，問題不是生硬的，是“認知困難”與“情感”相互作用的產物，問題解決需要重點突出試錯意味.

[關鍵詞] 初中數學;問題解決;教學論視角

初中數學教學中，問題解決被視為具有高度綜合性的過程，學生在問題解決中需要利用已有的知識或經驗，對面臨的問題進行抽象、建模，以實現問題的解決. 在核心素養被提出之后，研究者對問題解決進行了進一步理解與拓展，并將之放到了教學論的視角下進行研究，這樣的研究過程與結果給了一線教師很大的啟發，在此筆者試結合自己的教學經驗，談談教學論視角下對問題解決的進一步理解.

初中數學教學視角下的“問題”

問題在數學教學中無處不在，在學生的生活中也無處不在，當在教學的視角下觀照這些“問題”的時候，可以發現問題有著超越經驗的意義. 今天的數學教學強調生活與數學的聯系，而問題在這個聯系過程中也起著非常重要的作用. 于是就可以得出一個重要的結論，那就是學生在數學學習中，問題可以從生活中來. 當然，這里的問題是指數學問題，于是從生活中抽象出數學問題，就是數學教師的一個重要任務（這里所涉及的數學抽象，實際上就是數學學科核心素養的重要組成部分之一）. 問題除了從生活中來之外，自然也可以從邏輯推理中來. 很多時候我們在課堂上通過對前面知識的復習提出新的問題，實際上就是沿襲的這一教學思路.

從教學論的視角來看，我們仍然認為問題不能是學生直覺性的反應，而應當是“認知困難”與“情感”相互作用的產物.

我們可以通過“多邊形的內角和”的例子來理解這一闡述：學生在學習多邊形的時候，一個重要的知識基礎就是對三角形的認識. 學生理解多邊形本身并沒有困難，但在尋找多邊形內角和公式的時候會出現困難，這個困難主要體現在學生可以推出四邊形、五邊形的內角和，但對于普遍規律卻難以把握——這就是認知困難. 在產生這個認知困難之后，由于問題解決動機的驅動，學生的情感自然會處于一種疑惑、焦躁甚至是急躁的狀態，這種狀態對于問題解決來說并非完全是壞事，因為其極有可能轉化為學生解決問題的動力.

進一步研究表明，問題反映的是學習者“理想與現實的差距”，當一個問題出現在學生面前時，“理想”就是問題的答案，而“現實”就是問題的題設，題設與答案之間的距離，反映著理想與現實之間的差距. 從教學論的視角來看，當這個差距的縮短在學生的能力范圍之內時，學生解決問題的動機是最為強烈的，而這一認識與“最近發展區”理論又是異曲同工的，所以說教師在分析并幫學生厘清問題的時候，一個最基本的原則，就是要在把握學生認知的基礎上，判斷學生的現實與理想之間有多大的距離.

譬如上例中，學生的認知“現實”是對三角形內角和的認識，是知道多邊形可以“拆”成三角形，而“理想”則是如何尋找到一個一般性公式來描述多邊形的內角和. 其中的距離在于學生通過逐步列舉四邊形、五邊形等圖形的基礎上，猜想多邊形內角和表達式的共性，然后表述為（n-2）×180°. 這個猜想與論證的過程，對于大多數學生來說都不是太大的困難，因而這個理想與現實之間距離縮短的過程，就是學生可接受的，進而問題解決的過程通常就是成功的.

這里特別需要指出的是，數學學習的過程中，當學生能夠用數學語言來描述問題時，實際上已經經歷了一個從自身的經驗走向理性的過程，因此有人界定問題為“從經驗走向理性的橋梁”，筆者以為這樣的界定，也能夠給數學教學帶來很多有益的啟示——譬如這個橋梁如何搭成，又如何才能牢固等.

教學論視角下理解“問題解決”

目前對問題解決的普遍認識是，問題解決不是一個運用固定理論方法或固定程序，去實現從題設到結論的方法. 也就是說嘗試建立一套固定的、普適的問題解決的模式，是不可行的. 更多的時候，問題解決帶有“現象學”的意味. 在問題解決的過程中，由于學習者思維方式、經驗基礎的不同，具體的解決問題的心理過程是有著一些差異的. 但是，這并不意味著問題解決真的毫無規律可循，否則也就沒有教育、心理方面的專家對這一領域實施研究了.

研究表明，從教學的角度看問題解決，其具有試錯的特性. 應試形態下的初中數學教學，總追求學生在解題的時候思路正確且迅捷，這從應試的角度來說是必需的，而從學生思維發展尤其是核心素養培育的角度來看，則是不合適的. 因為學生在真正的問題（非完全指數學領域）解決過程中，總會經歷對問題的分析、判斷等過程，此過程中總有失誤的時候，關于這一點，問題解決研究者提出了“可錯性學說”，該學說認為“錯誤是件好事情”. 而在學生的學習過程中，錯誤其實也是難以避免的，作為數學知識、數學思想方法與數學思維綜合性很高的問題解決，避免出錯也是不可能的事情. 因此，在問題解決教學中吸納“可錯性學說”，將試錯當成問題解決的重要思路，也是可取的.

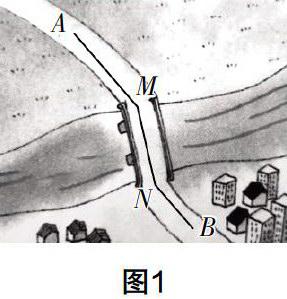
最具說服力的例子來源于教材上的一些“課題學習”，如人教版教材中的“最短路徑問題”，這是利用軸對稱知識來解決的一個問題，在對其中的“造橋選址問題”（如圖1）的分析中，筆者發現好多學生難以利用軸對稱知識建立直接的模型. 在建立模型的過程中，學生試圖通過軸對稱來尋找到最短的路徑，結果在畫圖的時候因為有“橋必須與河垂直”的要求，導致在草稿紙上畫出的圖形錯誤、修正、再錯……

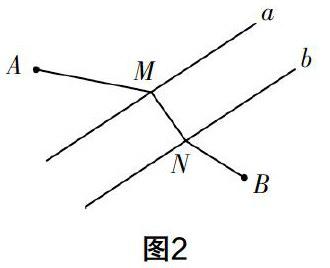
這種試錯在筆者看來是有益的，因為學生在試錯的過程中，必須完成數學抽象的過程，即將實物圖轉換為幾何圖形（如圖2），這實際上是在不斷地嘗試軸對稱知識在其中可以發揮什么樣的作用，同時也是對圖中AM+MN+NB最小值的不斷摸索. 當學生發現此問題解決的過程中不僅需要軸對稱，還需要平移，進而最終將問題轉換為：N點在直線b的什么位置時，所求距離是最小的？

這樣的試錯，實際上將學生的思維整個進行了一次梳理，學生所猜想的所有情形都出現了一遍，學生不僅知道了正確方法對在何處，也知道了錯誤方法錯在哪里. 這樣，學生思維中就既有對的認識，又有錯的認識，這樣學生的思維是全面完整的，問題解決的思路是全面清晰的. 教師在教學的過程中，只要重點強調一下正確思路，讓學生形成解題思路即可. 這樣的試錯過程，不僅不會影響學生的應試能力，還會因為其經歷了完整的、由錯到對的探究過程，從而保證學生的數學學科核心素養可以得到有益提升.

當然，問題解決的重心不只在試錯上，在問題解決的過程中，培養學生的創新思維、批判思維，讓學生在問題解決之后總結自己的思維過程，提取其中有益的那部分，讓學生從自己知識結構與方法完善的角度去思考問題解決的過程有哪些收獲，都是可以提升學生的問題解決能力的，都是可以培養學生的數學學習品質的. 這些方面其實都是問題解決研究的主題內容，而筆者在此重點強調試錯，是因為看到在傳統研究中這個話題有些薄弱，故重點強調.

“問題解決”之于教學的意義

問題解決能力無疑是學生應當具備的關鍵能力，這就是說在核心素養指引教育教學改革的背景下，問題解決將成為通過數學教學提升學生核心素養的重要途徑.

但這樣的表述仍然顯得過于籠統，從教學論的視角來看問題解決的意義，應當建構這樣的幾點認識：其一，問題解決可以讓教師更好地反思初中數學教學. 數學教學不是純粹地教數學知識，還要教會學生數學思想方法，讓學生學會用這些方法，而這個目標，只有在問題解決的具體過程中才能實現. 著名哲學家亞里士多德說過，“對于要學習才會做的事情，都是通過那些學會后應當做的事情來學習的”，這與中國常說的“在游泳過程中學會游泳”是一個道理，只有在問題解決的過程中才能培養問題解決能力，從而讓數學教師更好地認識到數學教學的價值. 其二，問題解決可以促進教師重構數學學科教學體系. 問題解決引導下的數學教學，可以讓教師形成問題解決導向的教學思路，從而讓學生的數學學習圍繞問題解決來進行，這樣可以讓學生的數學學習具有一個完整的問題解決情境，從而促成學生的問題解決過程.

總之，在教學論視角下，初中數學本著問題解決的思路去教學，可以促進教師更好地建立數學教學的思路，促進學生數學知識體系的建構，最終促進核心素養的養成.