根據(jù)歷史，重構(gòu)課堂

陳孝珍

摘 要：發(fā)生教學(xué)法的重點(diǎn)并不是對(duì)歷史的談?wù)摚窃趯W(xué)生具備足夠心理動(dòng)機(jī)時(shí)，適時(shí)對(duì)某個(gè)主體的精心講授。發(fā)生教學(xué)法在數(shù)學(xué)教學(xué)中進(jìn)行應(yīng)用時(shí)，教師應(yīng)注重學(xué)生對(duì)未知事物獵奇心理的保護(hù)，并在此基礎(chǔ)上引導(dǎo)學(xué)生對(duì)數(shù)學(xué)知識(shí)發(fā)生過程的經(jīng)歷與體驗(yàn)。

關(guān)鍵詞：發(fā)生教學(xué)法；實(shí)施；案例分析

個(gè)體發(fā)育史重蹈種族發(fā)展史這一觀點(diǎn)是德國(guó)生物學(xué)家海克爾（E.Haeckel）（1843—1919）于1866年提出的生物發(fā)生律。個(gè)體知識(shí)的發(fā)生過程遵循人類知識(shí)的發(fā)生過程這一教育教學(xué)中的規(guī)律也是海克爾生物發(fā)生律進(jìn)行應(yīng)用推理而得到的。將這些客觀的原理運(yùn)用于數(shù)學(xué)教學(xué)中，則個(gè)體對(duì)數(shù)學(xué)知識(shí)的理解過程遵循數(shù)學(xué)知識(shí)的發(fā)生發(fā)展過程這一規(guī)律也就不難理解了。

依賴歷史作為教學(xué)線索并使之對(duì)教學(xué)產(chǎn)生啟示的作用就是我們通常所說的發(fā)生教學(xué)法，發(fā)生教學(xué)法的重點(diǎn)并不是對(duì)歷史的談?wù)摚窃趯W(xué)生具備足夠心理動(dòng)機(jī)時(shí)適時(shí)對(duì)某個(gè)主體的精心講授。發(fā)生教學(xué)法應(yīng)注重學(xué)生對(duì)未知事物獵奇心理的保護(hù)，并在此基礎(chǔ)上引導(dǎo)學(xué)生對(duì)知識(shí)發(fā)生過程的經(jīng)歷與體驗(yàn)。本文以“有理數(shù)”第一章節(jié)中“正數(shù)和負(fù)數(shù)”這一知識(shí)點(diǎn)為例進(jìn)行發(fā)生教學(xué)法具體實(shí)施過程的討論與研究。

一、創(chuàng)設(shè)情境，引入新知

1. 舊知回顧

師：表示物體個(gè)數(shù)和事物順序而產(chǎn)生的諸如1、2、3、4……這些數(shù)叫作什么數(shù)呢？

生：自然數(shù)。

師：什么數(shù)被用來表示“沒有”？

生：自然數(shù)0。

師：對(duì)物體進(jìn)行分割或者測(cè)量時(shí)結(jié)果不是整數(shù)，又出現(xiàn)了什么數(shù)？

生：分?jǐn)?shù)（小數(shù)）。

師：這些數(shù)總共有多少個(gè)呢？

生：無數(shù)個(gè)。

師：請(qǐng)同學(xué)們觀察以下情境。

2. 課件出示情境

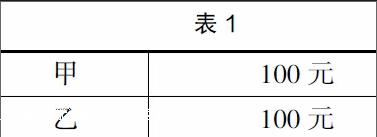
甲、乙兩人做買賣，甲賺了100元，乙虧了100元。

師：老師將兩人做買賣時(shí)的贏利與虧損用表格（表1）進(jìn)行表示，你們覺得合理嗎？

生：不合理。

師：雖然贏利與虧損的數(shù)額都是100元，但其所代表的含義是相反的，對(duì)于這樣一組相反意義的量，我們不能這么簡(jiǎn)單地表示。

3. 課件出示情境

請(qǐng)運(yùn)用以前所學(xué)的知識(shí)來解決以下問題。

（1）文具盒價(jià)值15元，李銘給營(yíng)業(yè)員20元，應(yīng)找回幾元？

（2）文具盒價(jià)值15元，李銘只準(zhǔn)備了10元，能買回這個(gè)文具盒嗎？為什么？

請(qǐng)列算式解答。

學(xué)生很快給出答案：20-15=5，15-10=5。

引導(dǎo)學(xué)生思考：第一個(gè)算式是李銘準(zhǔn)備的錢數(shù)減去文具盒的價(jià)格，第二個(gè)算式我們能否也這樣表達(dá)呢？結(jié)果會(huì)怎樣？

學(xué)生列出算式：10-15，但無法解答，很多學(xué)生表示“不夠減”。

數(shù)學(xué)相關(guān)歷史引申：

這樣類似的事情在生活中早就發(fā)生過，歷史上很多數(shù)學(xué)家也曾在這個(gè)問題的解答上表示過困惑。

歷史問題：早在公元3世紀(jì)，希臘數(shù)學(xué)家丟番圖就在自己的著作《算術(shù)》一書中表達(dá)過方程4x+20=4是不具備什么意義的。另外，斐波拉契（1170—1250）這位意大利著名的數(shù)學(xué)家在《花朵》中也表達(dá)了方程x+36=33沒有存在的依據(jù)，除非x所代表的這個(gè)數(shù)是人們欠下的3枚錢幣。

這些顯然都是不夠減的問題。

教師提問：對(duì)于情境（1）和情景（2）中所表達(dá)的賺100元、虧100元以及（20-15），（10-15），你用什么方式對(duì)它們進(jìn)行區(qū)分呢？

二、經(jīng)歷過程，自主探索

1. 大膽交流想法

（1）學(xué)生想出用不同的數(shù)字顏色、不同方向的箭頭、正負(fù)號(hào)等多種方法來表示“賺”與“虧”。

（2）對(duì)于錢數(shù)不夠時(shí)的表達(dá)，學(xué)生想出了用不同顏色、在5這個(gè)數(shù)字上做記號(hào)或者索性在5后面添上“不足”等字樣的諸多辦法。

2. 人類對(duì)負(fù)數(shù)表示方法的探索

數(shù)學(xué)家們?cè)诿鎸?duì)相反意義的量、不夠減這些問題結(jié)果的表示時(shí)也是頗費(fèi)周折的，他們也像學(xué)生們一樣想出了很多的辦法。魏晉時(shí)期的數(shù)學(xué)家劉徽提出了“正算赤，負(fù)算黑；否則以邪正為異”的做法，也就是說在遇到這類問題時(shí)采用紅色小棍代表正數(shù)、黑色小棍代表負(fù)數(shù)的表示方法，某些特殊的時(shí)候也可以用正放的小棍表示正數(shù)、斜放的小棍表示負(fù)數(shù)。不同顏色表示正負(fù)數(shù)的方式一直沿用至今，現(xiàn)在還經(jīng)常有經(jīng)濟(jì)出現(xiàn)赤字等表示收入小于支出的表達(dá)。另外，還有13世紀(jì)數(shù)學(xué)家李冶在《測(cè)圓海鏡》中將斜畫一杠用來表示負(fù)數(shù)的歷史事實(shí)記載等。除此以外，還有很多用文字表達(dá)負(fù)數(shù)的形式在古算中出現(xiàn)過，如不足、出、賣、付、弱等。

印度學(xué)者婆羅摩笈多在公元7世紀(jì)提出了用畫小點(diǎn)或小圈來表示負(fù)數(shù)的做法。荷蘭數(shù)學(xué)家吉拉爾在17世紀(jì)第一個(gè)提出了用“-”來表示負(fù)數(shù)的做法并得到了數(shù)學(xué)界的一致肯定，負(fù)數(shù)的表示方法到此時(shí)才算得到統(tǒng)一。

師：大家從歷史上數(shù)學(xué)家們的探索可以看出，他們的很多想法與同學(xué)們的表達(dá)方式是相似的，表達(dá)方式雖然各有不同，但其最終的目的都是為了可以區(qū)分正負(fù)數(shù)，都是為了新數(shù)的表示方法的探尋。現(xiàn)在大家來發(fā)表一下看法，你覺得哪種方式最好？

生：用加減號(hào)表示最好，簡(jiǎn)潔且意義分明。

師：對(duì)，17世紀(jì)荷蘭數(shù)學(xué)家吉拉爾提出的這個(gè)方式之所以得到大家的認(rèn)同，正是有這些方面的原因。以前人們更多的是把“+”“-”作為運(yùn)算符號(hào)來表示，后來因?yàn)橛辛诵再|(zhì)上的區(qū)別，“+”“-”也因此有了正號(hào)和負(fù)號(hào)的專屬稱謂。

師：投影練習(xí)——

（1）如果某店今日贏利300元用+300元來表示，那么虧損300元應(yīng)該用（ ）元表示。

（2）在行走時(shí)，若將向南走30米記作 +30米，則向北走30米應(yīng)該記作（ ）米。

三、抽象歸納，重新建構(gòu)endprint

1. 定義

諸如5、2.9%、4.8這些大于0的數(shù)都是正數(shù)，而像-5、-2.9%、-4.8這類在正數(shù)前加上“-”的數(shù)都是負(fù)數(shù)。有時(shí)我們?cè)诒硎菊龜?shù)時(shí)，為了強(qiáng)調(diào)這些數(shù)字所表達(dá)的意義，即使是正數(shù)，也會(huì)在這些數(shù)字的前面加上“+”。比如+5、+3.9其實(shí)就是5、3.9，“+”讀作“正”，但因?yàn)槠涮匦钥梢允÷圆粚憽６?”讀作“負(fù)”，是具備明確的意義與作用的，不能省略。

2. 教師任意寫出幾組正負(fù)數(shù)讓學(xué)生讀寫練習(xí)

3. 相反意義的量

師：具備相反意義的量在我們的實(shí)際生活中會(huì)經(jīng)常遇到。（投影）

（1）汽車向南與向北各駛出20千米；

（2）氣溫從零上3攝氏度下降至零下3攝氏度。

請(qǐng)學(xué)生根據(jù)自己的生活經(jīng)驗(yàn)舉出一些類似的例子。

和學(xué)生一起歸納小結(jié)：用來表示相反意義的量的詞一般有收入和支出，增加和減少，上升和下降等。

4. 找相反意義的量

師：與零上5攝氏度意義相反的量是什么？這個(gè)零上與零下是以什么來區(qū)分的？如何用正負(fù)號(hào)分別對(duì)它們進(jìn)行表示？

5. 學(xué)生動(dòng)手操作

師：現(xiàn)在老師為每位同學(xué)提供一個(gè)空白的溫度計(jì)表，每根刻度線之間相差1攝氏度，如果我們將最下面一根線表示為0攝氏度，請(qǐng)問這根線往上2格式是多少攝氏度呢？

生：2攝氏度。

師：請(qǐng)同學(xué)們依此往上標(biāo)到5攝氏度。

師：+5°C應(yīng)該在哪里？

在學(xué)生找到+5°C的位置之后，教師追問：-5°C呢？

師：根據(jù)我們之前的操作和觀察，可以發(fā)現(xiàn)這個(gè)空白的溫度計(jì)圖表上是沒有記錄零下溫度的，那么零度以下的溫度該怎么辦呢？可以在這個(gè)圖表中進(jìn)行表示嗎？如果可以，你覺得應(yīng)該怎樣表示呢？請(qǐng)同學(xué)們重新設(shè)計(jì)一下刻度，要使你最終設(shè)計(jì)的刻度既能顯示零上溫度，又能顯示零下溫度。

6. 交流和總結(jié)

當(dāng)學(xué)生對(duì)零上溫度、零下溫度以及0攝氏度的對(duì)應(yīng)刻度的位置確定以后，教師引導(dǎo)學(xué)生一起總結(jié)：零上溫度與零下溫度的位置應(yīng)該在0攝氏度的位置確定以后才能確定，0只是正數(shù)與負(fù)數(shù)的一個(gè)分界，所以0°C并非代表“沒有”，它也是一個(gè)確定溫度的表示。

四、 拓展延伸，鞏固內(nèi)化

1. 相反意義的量

師：如果一種意義的量規(guī)定為正并用“+”表示，那么另一種與之相反意義的量就可以為負(fù)并用“-”來表示。

師：比如，如果將往前走30米記作+30米（讀作正30米），那么往后退30米便可記作-30米（讀作負(fù)30米）。同理，請(qǐng)同學(xué)們回答以下問題：如果將火車向西行進(jìn)10千米記作+10千米（讀作正10千米），那么火車向西行進(jìn)-10千米的意義是什么呢？

生：向東行進(jìn)了10千米。

師：正負(fù)數(shù)前面的正號(hào)和負(fù)號(hào)都可以省略不寫嗎？為什么？

生：正號(hào)可以，負(fù)號(hào)不可以。正號(hào)省略后，其意義不會(huì)改變，而負(fù)號(hào)省略后就變成相反的意義了。

例題：張?zhí)m的體重一個(gè)月之內(nèi)增加了2kg，林華的體重在這個(gè)月內(nèi)減少了1kg，李剛的體重沒有變化。請(qǐng)分別寫出張?zhí)m和林華在這個(gè)月中的體重增長(zhǎng)值。

解：張?zhí)m、林華、李剛在這個(gè)月中的體重增長(zhǎng)值分別為：2kg、-1kg、0kg。

正負(fù)數(shù)在生活中的應(yīng)用十分廣泛，比如地形圖中某地區(qū)海拔高度的表示，我們可以將海平面的高度記作0 m，然后將該地區(qū)的高度與海平面進(jìn)行比較后用正負(fù)數(shù)表示。

2. 練習(xí)

假如一只動(dòng)物向南移動(dòng)了30米，我們將之記作-30m，那么+12m表達(dá)的是什么含義呢？如果這只動(dòng)物原地不動(dòng)，我們應(yīng)該怎樣用數(shù)字做標(biāo)記呢？

總之，教師在教學(xué)時(shí)要了解學(xué)生的原有學(xué)習(xí)基礎(chǔ)，采用新穎多樣的教學(xué)方法，開發(fā)學(xué)生的思維，充分發(fā)揮學(xué)生的主體作用，讓學(xué)生能夠主動(dòng)地學(xué)習(xí)。教師應(yīng)在課上及時(shí)檢查學(xué)生的學(xué)習(xí)情況，優(yōu)化學(xué)生的知識(shí)結(jié)構(gòu)和思維方式，以達(dá)成課堂教學(xué)目標(biāo)。endprint