小學五年級學生問題解決中幾何直觀能力的水平研究

唐平 付天貴

[摘 要]問題是數學的心臟，問題解決是數學學習的本質特征，幾何直觀是解決數學問題的重要方式，利用圖形去分析和描述問題，實現問題的直觀化表示是問題解決的重要途徑。由問題解決和幾何直觀的含義入手，分析得出小學五年級學生運用幾何直觀進行問題解決時存在感知、理解、把握和推理四個水平。

[關鍵詞]問題解決；幾何直觀；存在性

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）08-0010-03

一、問題解決的含義

數學家哈爾莫斯說：“問題是數學的心臟。”數學之所以成為鍛煉人們思維的“體操”，就是因為它總是不斷地提出問題和解決問題。數學問題解決（Problem Solving）或稱解決問題，是指利用某些方法和策略，使個人從初始狀態情境達到目標狀態情境的過程。數學問題解決過程是一個連續進行數學思維的過程：首先是引發問題，問題是在一定的情境中引發的，并且對學生來說要具有一定的思考價值；其次是解決問題，情境所引發的問題按照一定的目標，應用各種認知，經過一系列的思維操作，使問題得以解決。

問題解決是數學學習的本質特征。我國基礎教育數學課程改革非常重視學生問題解決能力的培養，把問題解決（解決問題）作為義務教育階段數學課程目標之一，并提出要培養學生發現問題、提出問題、分析問題和解決問題的能力，即通常所說的“四能”。數學問題解決的宏觀過程為：問題情境→轉換→尋求解法→求得解答。在轉換和尋求解法環節，幾何直觀被認為是常用的方法和手段。

二、幾何直觀的含義

直觀是指人用感官直接接受的、直接觀察的，即人們接觸事物時，借助于經驗、觀察、想象等產生的對事物及其關系直接的感知與認識。從狹義上理解，直觀是視覺化、形象化的，是通過對客觀事物的直接接觸而獲得的感性認識。幾何直觀主要是利用圖形來描述和分析問題，也就是通過圖形獲得的對所研究問題的數量關系和空間形式的視覺化的、形象化的認識。

20世紀最偉大的數學家希爾伯特在名著《直觀幾何》一書中說道：“圖形可以幫助我們發現和描述研究問題，能幫助我們尋求解決問題的思路，可以幫助我們理解和記憶得到的結果。”幾何直觀是數形結合思想的體現，通過圖形的直觀性質，可以闡明數與數之間、形與形之間、數與形之間的關系，實現代數問題與圖形之間的互相轉化和相互滲透，把抽象的數學問題具體化和形象化，是探求數學問題的重要途徑。正如荷蘭數學教育家弗賴登塔爾所言：幾何直觀能告訴我們什么是可能重要、可能有意義和可接近的，并使我們在課題、概念與方法的荒漠之中免于陷入歧途之苦。

三、幾何直觀能力水平的劃分

布魯姆（B.Bloom）、克拉斯沃爾（D.R.Krathwohl）等是較早研究教學目標分類的學者，他們在借鑒生物學動植物分類方法的基礎上，創立了目標分類理論。其中，認知目標分成識記、領會、應用、分析、綜合及評價六種水平。我國義務教育數學課程標準將課程目標分為知識與技能、過程與方法、情感態度與價值觀三個維度；另外，從學習角度出發，課程標準又將課程目標分為結果性目標和過程性目標。結果性目標分為了解、理解、掌握、運用四個水平；過程性目標用體驗、經歷、探索等動詞來描述，顯然也存在水平差異。

艾倫·霍弗（Alan Hoffer） 研究了幾何課程中的認知情況，指出其中存在5方面技能：視角方面技能、語言方面技能、繪圖方面技能、邏輯方面技能、應用方面技能。這5方面技能對應著5種能力，即視角技能→直觀能力、語言技能→口頭表達能力、繪圖技能→畫圖能力、邏輯技能→邏輯能力、應用技能→運用能力。顯然，Hoffer 所提出的幾何中的技能既是從不同角度去認識的，同時又有水平劃分。

幾何直觀是學生運用實物、符號、圖形描述問題，以及認知數學問題的能力。幾何直觀存在不同的形式，可以劃分為不同水平。以布魯姆認知分類目標理論和我國義務教育階段性結果目標水平的劃分為基礎，根據幾何直觀的內涵，結合Hoffer 對幾何中的技能水平的劃分，可以將幾何直觀能力水平劃分為感知、理解、把握、推理四個水平，建構如下分析框架。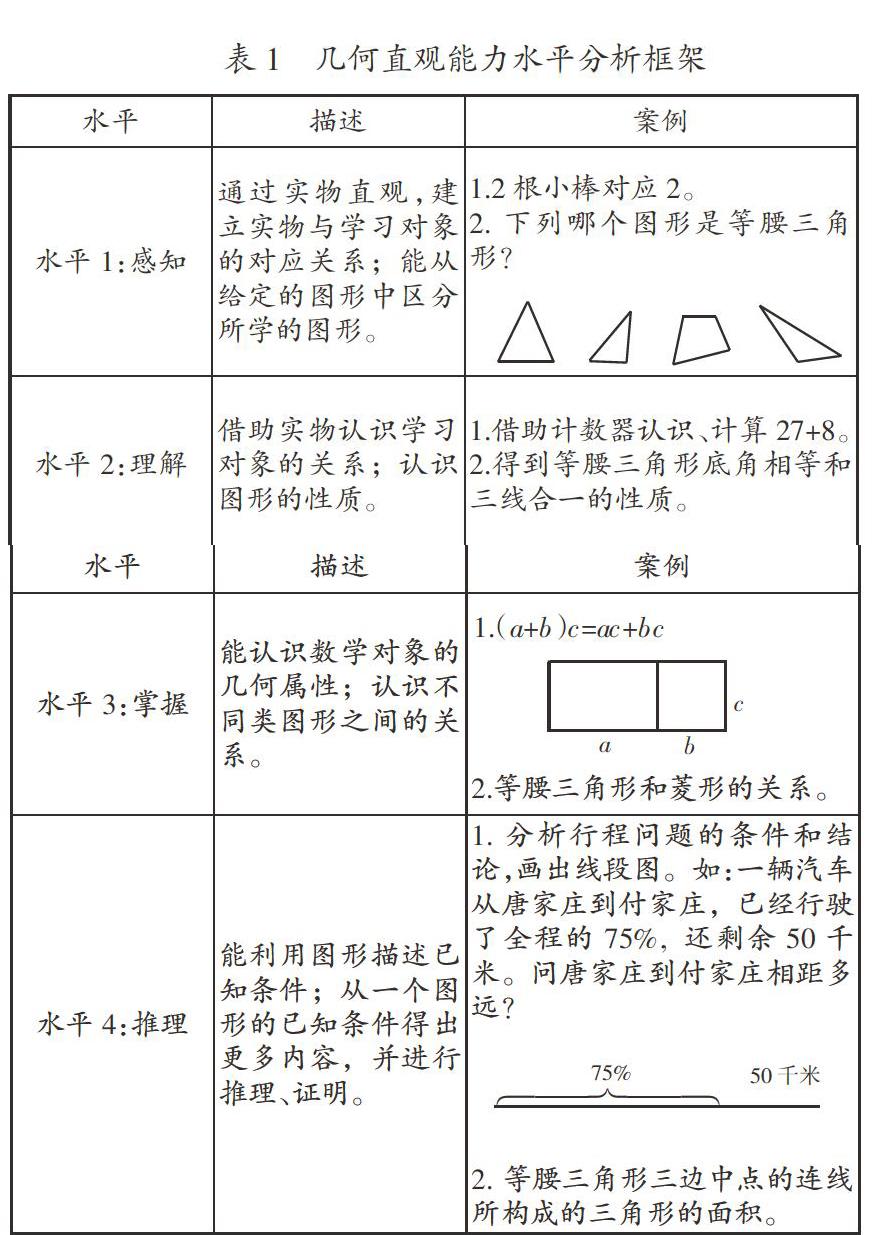

四、問題解決中幾何直觀能力水平的存在性

1.測試工具

自編《幾何直觀能力水平測試卷》，對問題解決中幾何直觀能力水平的存在性進行分析。初試卷由4個問題組成，每題5分，共20分，要求學生在20分鐘內完成。第1題是通過畫圖理解實際問題中的分數，第2題是通過圖形模式去描述整數的運算，第3題是對運算法則的深入理解，第4題是對數據的分析與描述。前三題是數與代數領域的內容，明確要求畫圖說明，第4題是統計與概率內容，要求用統計圖表去描述和解決問題。試卷編制過程中，特別邀請了一線教師和研究員進行編制和修改，以確保試題的效度。

2.工具的信度

試卷編制完成后，對重慶市某區小學五年級60名學生進行預測，并邀請參與試卷編制的一位小學數學教師統一評分，然后利用SPSS.20對數據進行分析處理。各測試題中，學生的平均得分和對應的標準差見表2。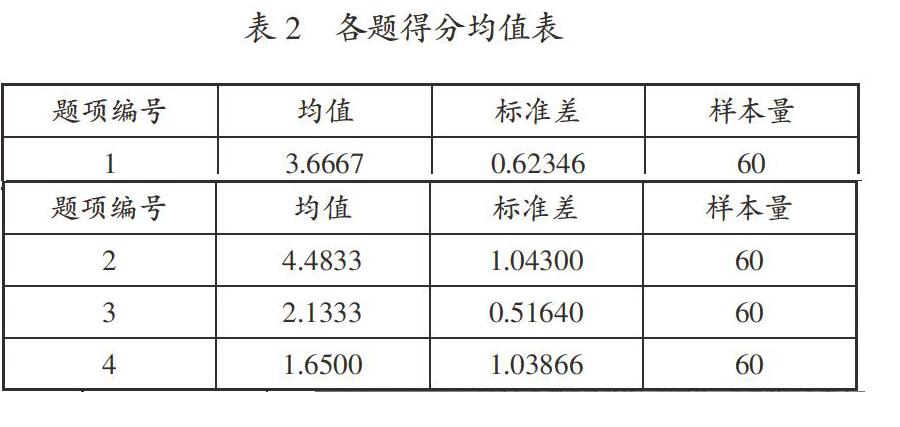

在利用SPSS.20進行信度分析時，先在模型框選擇Cronbach's Alpha系數，即α系數，然后在各題項之間選擇相關系數，置信區間和檢測值選擇系統默認值，就得到各題項的相關系數（如表3）：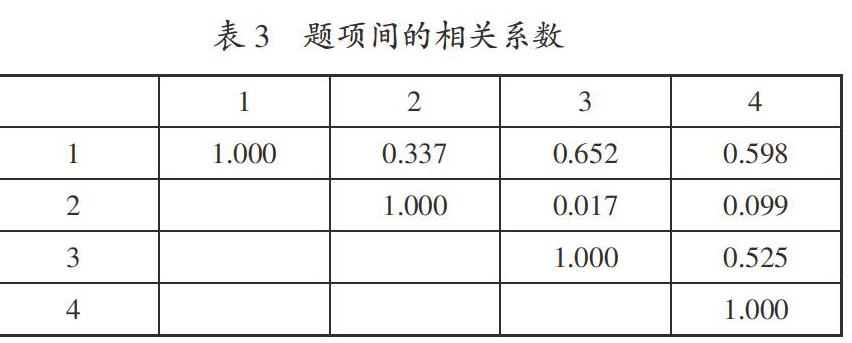

測試卷的Cronbach′s Alpha系數為0.670，基于標準化項的Cronbach′s Alpha系數為0.693。從表3可以看出，第2題與第3、4題的相關性較低。第2題是有關分數的認識，測試學生運用圖形直觀描述分數的能力。從初試情況看，學生都能通過實物直觀建立實物與學習對象的對應關系，說明學生都能達到幾何直觀的感知水平，把該題編入測試卷意義不大。刪去該題，重復上述過程，計算出由第1、3、4題組成的測試卷的系數為0.788，基于標準化項的系數為0.818，這樣的測試卷信度較好。

3.測量結果

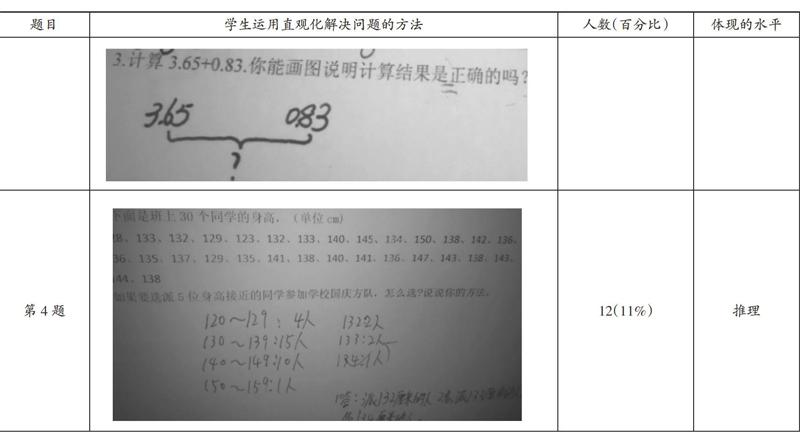
正式測試對象為重慶某區小學五年級學生（105人），其中城市學生60人，鄉鎮學生45人。為了減少測試卷對學生的影響，我們把測試內容編入學生的單元測試中，讓學生在正常的課堂狀態下進行測試，測試題在單元測試卷中處于計算題的第2、3、4題。學生運用直觀化策略解決各問題的主要方法統計如下：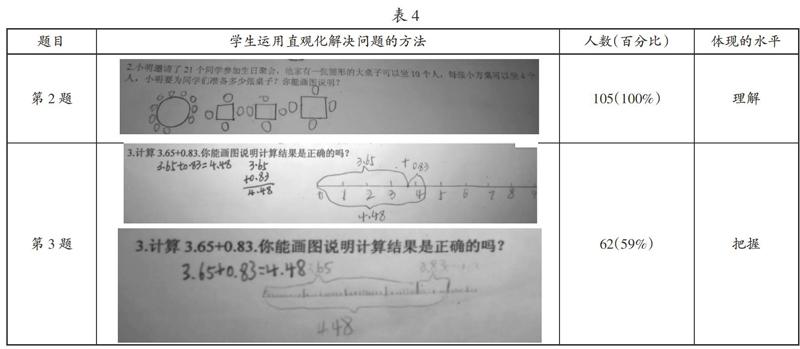

4.分析與討論

問題解決時必須理解問題情境中的具體關系，才能選擇適合的圖形去表示，這一能力水平稱為幾何直觀的理解水平。例如第2題是考查學生對整數及運算法則的理解，通過畫圖，把客人數和所需要的不同的桌子數直觀表示出來，體現了學生的思維過程。從統計情況看，小學5年級學生基本上都能達到這一水平。

第3題是考查學生對小數和小數運算法則的理解和描述。分析測試結果后發現，主要存在兩種情況：第一種是只運算，沒能畫圖，這樣的學生有43人，占41%；第二種是通過畫線段圖來表示，這樣的學生有62人，占59%。畫線段圖時，有的學生能畫出整數部分，也有的學生能畫出小數部分，但都沒能正確用線段圖表示運算法則。在問題解決中，必須把握具體情境中數學對象的幾何屬性，只有掌握了對象的幾何屬性，問題解決時才能正確進行直觀表示，這一能力水平我們稱之為幾何直觀的掌握水平。從測試情況看，只有一半的學生達到該能力水平，造成這個現象有兩個方面的因素：一是小學數學教材通常是讓學生通過單位換算去認識小數的，如人民幣1元5角可以表示為1.5元，從而引入小數，缺乏引入小數必要性的介紹以及怎么理解小數的直觀表示；另一方面是由于學生之前已經學習了分數，教師往往只強調運算而忽視對算理的直觀表示。

統計與概率這一題沒有明確要求學生用畫圖的方式對問題進行描述，但學生必須運用統計表或是統計圖對數據進行描述，然后回答問題。學生解決問題的方法主要有三種：一是放棄回答，有20人，占19%；二是通過觀察數據，選擇身高比較接近的5人作為答案，采用這種方式回答的有73人，占69%；三是沒有列表，但進行了分段統計，具備用統計表描述問題的思想，采用這種方法描述問題的有12人，占11%。運用幾何直觀進行推理，是幾何直觀的推理水平。從測試結果看，雖然學生已經學習了統計表和條形統計圖，但缺乏運用統計表和統計圖描述數據、分析問題的意識，主要是因為課程標準對該部分的要求是給定統計表和統計圖后能完成相應的問題，因此教材都是直接給出統計表和統計圖，這讓學生難以體會到運用統計表和統計圖去描述問題的必要性。

在范希爾（Van Hiele）夫婦提出幾何思維模式后，學者們對幾何思維從不同層面進行了研究，雖然不同學者對幾何思維水平的劃分不盡相同，但都證實了幾何思維水平層次的存在性。布格（Burger）和桑尼斯（Shaughnessy）認為“數學思維既是連續的，也是動態變化的，每一個水平都取決于對前一個水平的掌握”，證實了小學生問題解決中幾何直觀水平的存在性，學生運用幾何直觀進行問題解決時存在感知、理解、掌握和推理四個水平。

[ 參 考 文 獻 ]

[1] 喻平.數學教學心理學[M].北京：北京師范大學出版社，2010.

[2] 教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[3] 安德森著.布盧姆教育目標分類學：分類學視野下的學與教及其測評[M].蔣小平譯，北京：外語教學與研究出版社，2009.

[4] Alan Hoffer著，宗岳譯.幾何不僅限于證明[J].教學與研究，1982（3）.

[5] 史寧中，孔凡哲.關于幾何直觀的含義與表現形式[J].課程.教材.教法，2012（32）.

【本文系基金項目“2015年教育部人文社會科學研究青年基金項目——小學生幾何直觀能力的形成與發展研究”（項目編號：15YJC880076）的研究成果之一。】

（責編 金 鈴）