“易數學”：哲學視域中的實踐創生

摘要：在“易思想”的哲學視域中提出“易數學”的教育主張，引領學校數學課程的創新與發展。“易數學”課程在目標建構上立足學科本體、實踐主體、能動個體，在內容創生上注重資源的融通匯合、教材的融會貫通、練習的融為一體，在課堂實施中關注個體學習、同伴學習、社群學習，建構了“易數學”的“學習-對話”模型。

關鍵詞：易數學；目標；內容；實施；數學教學

中圖分類號：G420 文獻標志碼：A 文章編號：1673-9094（2018）04A-0017-05

在中國傳統文化中，易是一種哲學思想。“易”者三義，一曰簡易，二曰變易，三曰不易。簡易是樣態，變易是方式，不易為核心。變易與不易，看似矛盾對立，實則有無相生、缺一不可，可謂相輔相成、辯證統一。

以“易”作為數學教育哲學，一是基于對中華優秀傳統文化的傳承，二是基于對教育教學規律、學科教學本質、兒童成長規律的把握，既具有文化傳承性又具有時代發展性。

以“易思想”審視數學教育教學，我們可以清晰地感受到：“變易”直觀表達了萬事萬物的運動與變化屬性，也蘊含著教育的發展性與兒童的生長性；“不易”集中體現了規律的確定性與恒常性；“簡易”含蓄道出了“大道至簡”的追求。

在“易思想”的視域中，“易數學”之“易”意為：一為簡易，刪繁就簡、化繁為簡，解決結構與流程的問題；二為變易，改良升級、變革優化，關注過程與結果的創新；三為不易，聚焦核心素養的提升、基于兒童主體的立場、立足數學學科的本質不易，遵循教育與兒童成長的規律。

我們所理解的“易數學”課程，是有根（源于兒童生活，基于學生實際）、有魂（聚焦學科本質，指向核心素養）、有趣（不僅有意義，而且有意思）的數學課程，是易學（易于主動學習）、易用（易于推廣應用）、易創（易于師生創生）的數學課程。

一、目標建構：立足三個“體”

在“易思想”的觀照下，我們從“學科本體”“實踐主體”“能動個體”三個層面對“易數學”課程目標體系進行了整體解讀。

對于數學這一“學科本體”而言，就小學來說，無論是基本概念還是基本法則，無論是自然數、整數、負數、分數、小數還是點、線、面、體，無論是加減乘除還是運算定律、面積體積計算公式，都需要把握住最基礎、最本質的核心內容進行目標建構。辯證看待變易與不易的關系，尋找到知識的生長點、經驗的遷移點與結構的連接點，進行根目標的建構，進而在根目標的基礎上延展出可生長的枝干目標群。

對于教師這一“實踐主體”而言，在“易數學”的課程目標設定時需要進行四個方面的立體思考與整體建構。第一個方面是教育哲學，解答“為什么培養人”這一核心問題；第二個方面是學科哲學，回答“數學究竟是什么”這一本源問題；第三個方面是核心素養，重點解決“培養什么樣的人”這一基本問題；最后一個方面是學科素養，研究“學科核心素養是什么”這一焦點問題。從教育哲學、學科哲學、核心素養及學科素養四個方面進行探問與追索，從而形成關于教育、數學、數學教育、數學教學的自我回答。

對于學生這一“能動個體”而言，“易數學”的目標需要從群體到個體進行結構化思考。對于學生群體來說，“易數學”目標應該是一個系統的目標集合群。既有基于全局視野的數學課程標準整體目標的校本化解讀，也有基于全程視線的各個學期目標的系列化建構。對于學生個體來講，“易數學”目標則是一條動態的目標生長線：既有基于學生當下基礎目標的適切建構，也有指向學生未來發展目標的長程設計；既有基于普適目標的個別化調整，也有基于進步曲線的超越式更新。

通過廣泛的學習與調研、研究與對話，我們將“易數學”的課程總體目標確定為培養數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析六大核心素養，引導學生培育數學的理性精神與嚴謹態度，會用數學的眼睛觀察現實世界，會用數學的語言描述現實世界，會用數學的思維思考現實世界，會用數學的方法探索現實世界，會用數學的技術改變現實世界。根據整體目標框架，逐步建構起各個年段、各個學期、各個單元，進而到各個課時的目標群與目標鏈。

二、內容創生：用好三種“鏡”

“易數學”的課程內容在設計與實踐時借鑒“二八原則”進行，約80%的蘇教版教材基礎內容加上約20%的各類資源拓展內容，既保證了基礎性內容的達標，又實現了拓展性內容的增能。

1.用好“廣角鏡”：資源可以“融通匯合”

一是對不同版本教材進行優勢組合。對于數學教學而言，“一標多本”給教師提供了多視角、可借鑒的教材資源庫。每一個版本的教材編寫都有其特點與優點。同一內容，各個版本的編寫思路可能就完全不同。如：《乘法分配律》的編排，蘇教版教材是在學生熟悉的跳繩情境中進行的，關注的是情境中幾個幾的乘法意義；北京師大版教材是圍繞生活中墻面貼瓷磚這一實際問題展開的，求長方形面積的兩種不同思路直觀而可視。當教師具有多版本視野時，就能引領學生跳出教材學數學。在多變的呈現方式背后，更清晰地感受到數學的核心與本質，從而抓住關鍵與根本，對不同版本的內容進行適度融合，形成更為適合本班學生的數學內容表達。

二是對數學繪本、故事進行優選融合。數學教師可以借助教研組的力量，在海量的繪本與故事資源中，進行優選組合，形成與教材配套的數學繪本故事資源庫，從而將適宜的數學繪本與數學故事引入課內學習與課外閱讀。如：在四年級教學《角》這一單元時，認識角時可以引入《兩條射線手牽手》這一數學繪本；而在探索角的大小與邊的長短無關而與兩邊叉開的大小有關時，可以加入《角兄弟》這一數學故事。

三是對自編數學童話進行優創整合。童話是兒童耳熟能詳且非常喜歡的文學體裁，當它與數學相遇時，往往就能發揮出1+1>2的作用。自2014年起，王嵐數學名師工作室的全體成員，合作共同完成了與最新版蘇教版小學數學教材配套的《小羅庚》《叮當歷險記》《古城西安游記》《魔法森林》等12本數學童話故事。這些數學童話故事一經使用，立刻受到了學生們的熱捧。這些數學童話故事，既可以作為課前預習的材料，又可以作為課中指引的讀本，還可以作為課后復習的資料，為學生提供了學習的導航圖與研究的預覽圖。

四是對數學實驗手冊進行優化結合。強調具身學習的重要性，引導學生在“做中學”中“做數學”。重視教材中配套數學實驗的組織與實施，同時加入“義務教育數學實驗資源開發與建設”總課題組，共同開發并運用與蘇教版教材配套的12冊《數學實驗手冊》。引導學生自主提出實驗猜想、合作進行實驗驗證，并最終得出實驗結論。在借助實物進行操作實驗的同時，也可以引入技術手段進行模擬實驗。如：驗證三角形的內角和是180°。傳統教學中，往往是通過測量三角之和相加，或將三個角拼成平角進行驗證。而借助幾何畫板這一軟件進行模擬操作實驗，學生通過點擊鼠標拖拽三角形的任意一個頂點，就可以直觀地看到無論三角形的形狀發生什么改變、三角形的三個內角度數如何發生變化，三角形的三個內角的和始終是180°。這樣的模擬實驗，因其實驗數據的隨機性與可變性、實驗結果的穩定性與具象性，更具說服力。

2.用好“透視鏡”：教材可以“融會貫通”

一是主題塊的橫向銜接。對于蘇教版教材中橫向的兩個或多個知識點進行整體連接，形成集約化的結構化設計，從而溝通看似不同知識點之間的內在聯系，引導學生發現“變易”中的“不易”。如：數學教材中，關于數的加減，有整數的加減法、分數的加減法和小數的加減法。這些加減計算，外在的形式看似并不完全相同，整數加減法是數位對齊也就是末位對齊，分數加減法需要轉化為同分母后進行計算，小數加減法是數位對齊也就是小數點對齊。這三者之間，整數加減法與小數加減法，聯系似乎更為緊密。然而在進行小數加減法計算時，仍然有部分學生受整數加減法末位對齊這一經驗的干擾而形成負遷移。進行主題塊的橫向銜接之后，整數、小數及分數加減法都可以統一到“相同計數單位才可以直接相加減”這一更為上位的規則之中。在此上位規則的統領下，整數加減法、小數加減法需要數位對齊后再相加減，異分數分數需要通分后轉化為同分母分數再進行加減，對于學生而言就不再僅僅是一種規定的算法，而是合乎基本算理的變式表達。這樣的尋根求源，經歷了化散為聚，實現了以一抵多。

二是主題鏈的縱向承接。同樣，對于教材中縱向的兩個或多個內容知識點，也可以通過其內在的邏輯關系，尋找到鏈接點與生長點，引導學生發現“不易”中的“變易”。如：認識整萬數和認識整億數，在教材中是兩個不同課時的內容。在“易思想”的指導下來關注這兩個內容，我們會發現其縱向上有著明顯的承接關系。認識整萬數，對于學生而言，是一次認識上的飛躍，從“一個一個數、十個十個數……”進而到“一萬一萬地數”，需要學生在“滿十進一”這一十進制計數法則的基礎上，聯系“個、十、百、千”，對應地創造出“萬、十萬、百萬、千萬”這四個計數單位。并且在此基礎上，完成對“個級”和“萬級”的認識。而認識整億數與認識整萬數，其方法論與知識體都是一脈相承的。完全可以通過整萬數的建構經驗，自主衍生出“億、十億、百億、千億”這四個計數單位，進行完成對“億級”的認識。而這樣的滿十進一、四位一級的經驗型創造，還會引領學生繼續探究，比千億更大的計數單位是什么？億級左邊還有什么數級？進而自主在課外拓展研究與學習“兆”“京”等等的計數單位。主題鏈的縱向承接，承接的不僅是知識、是內容，更是結構、是方法，是數學思想的生本化表達。

三是主題群的立體對接。主題群超越了單一維度的主題塊及主題鏈的概念，既可以橫向發生聯系，又可以縱向加以推進。在主題群的立體對接中，既可以是基于教材的整體內容進行系列設計，也可以是基于學生的生活實際進行項目推進。如“運算律”這一內容就可以進行主題群的整體設計。首先設問：加減乘除這四則運算，是否都有交換律？進而通過系列化的提出猜想、舉例驗證、得出結論，最終發現在小學范圍內加法和乘法具有交換律，而關于減法和除法提出的猜想與實際例證并不相符。同時，在此基礎上，發現兩個數具有加法交換律、乘法交換律，在三個數、四個數、五個數……中，加法交換律與乘法交換律仍然成立，進行縱向延伸。換一個角度進行思考，還可以進行橫向推廣，思考三個數相加、相減、相乘、相除是否具有結合律，再次經歷猜想與驗證、結論與運用的過程。又如：在學校組織郁金香節系列活動時，我們數學老師就可以根據這一主題組織學生開展項目化學習，將體積的測量、質量的測量、高度的測量、時間的記錄、數據的收集與整理、統計圖的繪制與分析等內容巧妙對接。學生通過對多個郁金香種球進行跟蹤研究，比較郁金香種球的體積或質量，在同樣的光照、土壤、天氣、水、肥料等條件下，提出系列猜想。對比這些郁金香的發芽時間、植株高度、開花時間等，制作復式折線統計圖，回看當初提出的猜想是否具有普遍意義。通過標準化的對比實驗與大樣本的數據采集，形成屬于自己的理解。

3.用好“顯微鏡”：練習可以“融為一體”

一是立足細微，深度解讀。將教材的某一個習題，深讀、精讀、反復讀，用足、用好、用到位，以極簡代替繁復，就能達到以一當多的效果。如蘇教版教材中有一道練習題，主要內容是：一枚1元的硬幣大約重6克，1億枚1元的硬幣大約重多少噸？如果僅僅將目標鎖定在學生通過計算選擇正確的答案，那就真可謂一葉障目而不見整片森林。如果教師能夠用好“顯微鏡”，深度解讀并改良優化，就能把簡單的計算、枯燥的數據與鮮活的經驗、豐富的體驗對接起來。在學生選擇600噸后，不妨繼續追問：“如果用載重量為5噸的卡車來運輸這些硬幣，需要多少輛？”當120輛卡車這一數據形象化地呈現在學生頭腦中時，遠比600噸的數據來得真切與實在，以致學生都不由自主地發出驚嘆：“1億枚硬幣真重呀！”這時候，再來一次適時追問：“一枚一元硬幣大約厚2毫米，猜一猜，1億枚一元硬幣疊加起來有多高？可以試著與珠穆朗瑪峰的高度進行比較。”又會引發學生驚異不已的感嘆：“1億枚硬幣疊放太高啦！”這樣的體驗與感悟，看似乃題外之意，實則乃數學核心素養的應有之義。

二是聚焦變式，廣度拓展。一個好的練習，往往不是孤立的，而是立于系統之中的。因此，在解讀各類練習時，往往需要一組一組對比著觀察與思考。在教材現有的編排中，這樣的以“組”為單位呈現的練習可謂比比皆是，如乘法數量關系與除法數量關系的比較、單位1已知與單位1未知的題組等等。同樣，在設計與組織練習時，也需要教師甚至師生共同進行變式創造，從而引導學生在萬變中尋找其宗。如：教材中，對于平面圖形與立體圖形的關系，就可以借助平面圖形進行系統建構。一個長方形，既可以通過平移，形成長方體。也可以一邊為軸旋轉360°，形成圓柱。一個圓形，同樣也可以通過平移，形成圓柱體。也可以直徑為軸旋轉180°，形成球。一個三角形、一個等腰梯形也可通過平移或旋轉形成立體圖形。在這一過程中，學生就在不同的介質中，尋找到了開啟平面圖形與立體圖形通道的基本方式——平移與旋轉。平移與旋轉前后，數據的聯系與變化，平面圖形與立體圖形之間的溝通與聯系，就在多樣的變式、廣度的拓展中，不斷清晰與明朗起來。

三、課堂實施：關注三種“學”

課堂的本源意義，在于學生主動學習與深度學習的真實發生。需要教師從關注“這個班”到關注“這一類”，進而走向關注“這一個”。因此，我們著力研究學習共同體中“人與自我”“人與他人”“人與社群”的關系。提出了三種“學”，聚焦“個體學習”“同伴學習”“社群學習”三大維度中每一位學生的學習與發展。

“個體學習”也稱“個學”，強調自我學習。引導學生關注自身，與自我對話，倡導自我反思。每一個人都需要正確認識自我，并借助自我的力量實現不斷自生長。個體學習，恰恰是給學生提供了足夠的自我認識、自我提升、自我反思的時間與空間，從而培養獨立學習、獨立思考、獨立表達的意識與能力。事實上，教育與學習的真正意義就是讓每一個人成為“自己”，成長“自己”，成就“自己”。

“同伴學習”也稱“互學”，強調從游學習。引領學生協同學習，與同伴對話，相互引領啟發。梅貽琦先生曾經形象地描述“從游”關系：“大魚前導，小魚尾隨，是從游也。”同伴學習、同桌互學，是學習階段發生頻率最高的協同式學習。有成果相互分享，有疑惑相互啟迪，有收獲相互碰撞，真正讓同學成為“同學”。這樣的追從、師從的過程，正是同伴間互為榜樣、共生同長的過程。

“社群學習”也稱“合學”，強調合作學習。指導學生小組學習，與團隊對話，實現差異引領。建構4人或6人異質小組，小組分工根據需求進行，組長可以輪值，根據學習任務的不同設立觀察員、操作員、記錄員或辯題的正反方陳述者等。通過指向共同目標的任務合作、議題討論、疑難會診等，提升每一個成員的學習力、思考力、表達力以及對于組織的貢獻力。

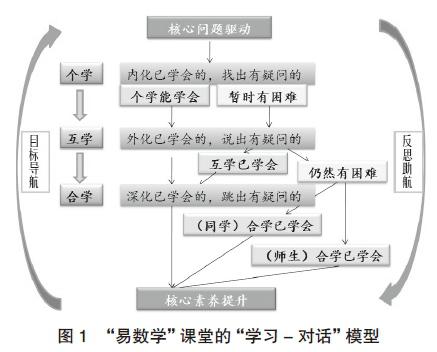
在這樣的背景下，我們提出了“易數學”的“學習-對話”模型（如圖1），以核心問題驅動為特征，以核心素養提升為導向，以對話交流為方式，以主動學習為樣態，即“個學：與自我對話；互學：與同伴對話；合學：與團隊對話”，借助學與教的對換、學與學的互助，實現課堂教學的轉型。

個學：內化已學會的，找出有疑問的。互學：外化已學會的，說出有疑問的。合學：深化已學會的，跳出有疑問的。“個學”自主能學會的，在“互學”中充分分享，“個學”自主有疑問的，在“互學”中充分交流。“合學”環節，由組長組織開展系統性交流，整體對核心問題進行不同維度、多種方式的個性解讀，對于互學中有疑問的部分重點開展交流。合學展示環節，由不同組的同學進行主題性介紹與補充性分享。對于仍然有分歧、有疑問的部分，教師主動介入，進行指導性交流。最終，形成對于該核心問題的整體認知。

而在聚焦“三學”的過程中，“學”——多樣的學、豐富的學、可變的學、真正的學，成為了核心與關鍵。教師成為了導學者、助學者，學生成為了自學者、互學者。在這樣的課堂中，每個人的學習起點是有差異的，每個人的學習方式是有差異的，每個團隊的表達是有差異的，……但這樣的差異成為了最可寶貴的資源。導學與助學的一個重要關鍵點就是關注差異背后的相同。學生能夠在不同中尋找相同，也就是在多樣的變化尋找到了不變的數學的規律、方法與思想。

責任編輯：楊孝如

“Yi-Mathematics”： Practical Creation in the Perspective of Philosophy

WANG Lan

（Primary School Attached to Changzhou University， Changzhou 213161， China）

Abstract： In the philosophical perspective of “Yi-thoughts”， “Yi-mathematics” is proposed as an educational idea， which can guide the innovation and development of mathematics in school. The goal of “Yi-mathematics” is based on courses themselves， practical subjects and enabling individuals. Also， its creation of contents attaches importance to confluent infusion of resources， integration of teaching materials， and unity of exercises. Meanwhile， it focuses on individual learning， peer learning and group learning in class， finally having constructed the model of learning and dialogue in “Yi-mathematics”.

Key words： Yi-mathematics； goal； content； implementation； mathematics teaching