“問題引領”下的課例研究

武前煒

摘要：在旋轉(zhuǎn)問題的教學中，著眼于概念課教學，以概念形成過程的介紹、數(shù)學思想方法的滲透、學生核心素養(yǎng)的培養(yǎng)為主線，用適當?shù)膯栴}引領學生共同思考，為學生提供更多動手操作的機會;借助于操作引導學生主動參與探索，并及時抽象概括，培養(yǎng)學生積極探究，主動獲取知識的素養(yǎng)和能力。

關鍵詞：旋轉(zhuǎn)?概念教學?動手操作?問題引領

近日，筆者執(zhí)教了一節(jié)九年級校際公開課——滬科版《24.1旋轉(zhuǎn)》第一課時，在教學過程中，著眼于概念課教學，以概念形成過程的介紹、數(shù)學思想方法的滲透、學生核心素養(yǎng)的培養(yǎng)為主線，用適當?shù)膯栴}引領學生共同思考，圓滿完成本節(jié)課教學目標。下面筆者就結合課堂實踐談談“問題引領”的概念教學。

一、教學簡錄

1.問題情境，引入旋轉(zhuǎn)

問題1：“假如世界沒有了轉(zhuǎn)動，我們的生活會有什么影響？”

眾生指出日常生活中存在轉(zhuǎn)動：水龍頭、電風扇、汽車輪子、雨刮器、鐘表、汽車方向盤。

學生：如果沒有旋轉(zhuǎn)，我們的生活會有很多不便。

教學分析：利用學生日常生活情景，激發(fā)學生興趣，點燃其求知欲，讓學生經(jīng)歷在現(xiàn)實生活情境中抽象出的數(shù)學問題，讓學生們認識到現(xiàn)實生活中蘊含著大量與數(shù)學有關的問題。

2.觀察交流，歸納旋轉(zhuǎn)

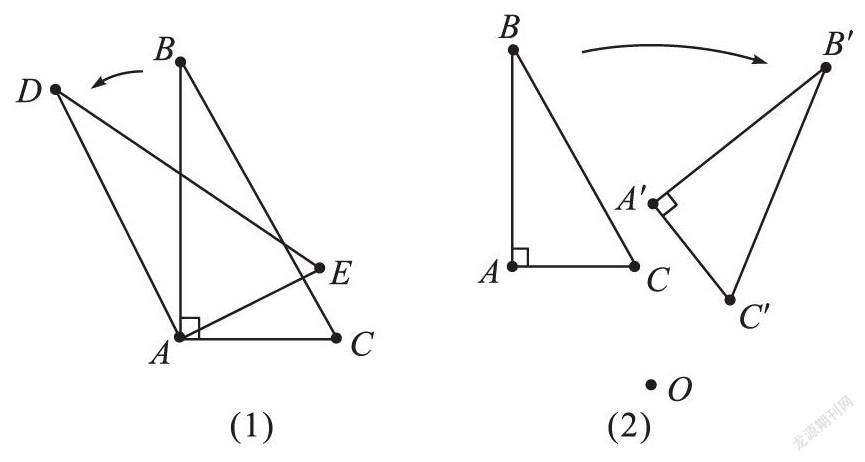
問題2：幾何畫板展示了兩組圖形的變換，觀察兩次作圖有什么共同特點。

都有一個定點：第一個圖A點，第二個圖O點;都有特定方向：第一個圖逆時針，第二個圖順時針;角度不一樣：第一個圖轉(zhuǎn)角度小點，第二個圖轉(zhuǎn)動角度大點。

旋轉(zhuǎn)三要素（板書）：定點→旋轉(zhuǎn)中心，方向→旋轉(zhuǎn)方向，角度→旋轉(zhuǎn)角度。

問題3：你能根據(jù)剛才的觀察交流歸納出旋轉(zhuǎn)的定義嗎？

生1：“一個圖形圍繞定點，轉(zhuǎn)動一個角度得到一個圖形叫旋轉(zhuǎn)。”

生2：“一個圖形繞著一個定點，按一定方向，轉(zhuǎn)動一個角度得到一個圖形叫旋轉(zhuǎn)。”

問題4：大家都同意他們的說法嗎？

剛才老師的圖形變換是在黑板平面演示的，所以定義要加上在“平面內(nèi)”。

定義板書：在平面內(nèi)，一個圖形繞著一個定點，按照一定方向，旋轉(zhuǎn)一定角度得到另一個圖形的變換叫旋轉(zhuǎn)。

問題5：圖（1）中的三角形誰是旋轉(zhuǎn)角？

∠BAD，∠CAE，可以用量角器測量出角度。

問題6：圖（2）中的三角形旋轉(zhuǎn)了多少度？哪個是旋轉(zhuǎn)角？

∠AOA′，∠BOB′，∠COC′，可以用量角器測量出角度。

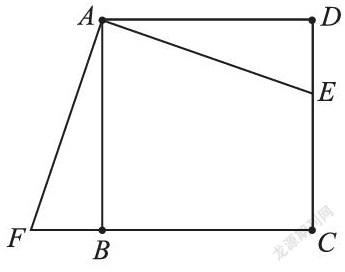
（幾何畫板展示）正方形ABCD邊長為3，且DE=1;△ABF是△ADE的旋轉(zhuǎn)圖形。

（1）旋轉(zhuǎn)中心是哪一點？

（2）旋轉(zhuǎn)了多少度？

（3）連接EF，△AEF是什么三角形？

問題7：圖（2）中有幾個旋轉(zhuǎn)角？怎么找到的？

“三個，找到對應點后與旋轉(zhuǎn)中心連接所成的角。”

問題8：圖（2）中能找到幾個對應點？

學生議論紛紛，有說三個，有說很多……

三角形在轉(zhuǎn)動中每個點都在轉(zhuǎn)動，也都有對應點，所以有無數(shù)對應點，那他們與旋轉(zhuǎn)中心所成的角會是多少呢？我們用幾何畫板驗證一下，得出結論：這些角度也等于旋轉(zhuǎn)角。

教學分析：通過學生直觀判斷和同學交流，歸納、概括和深刻理解旋轉(zhuǎn)角概念，通過老師富有深意的問題，學生的學習熱情很快被點燃，其已有的知識經(jīng)驗與活動經(jīng)驗被充分喚醒。

3.分析類比，認識旋轉(zhuǎn)

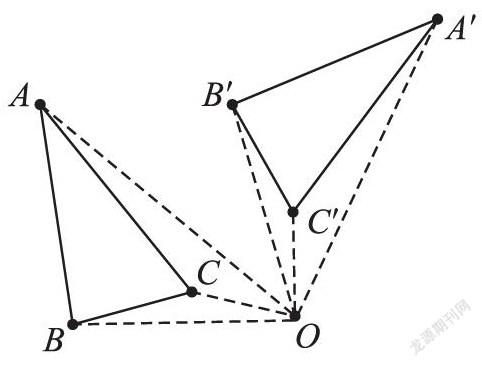
幾何畫板演示△ABC繞點O轉(zhuǎn)動，觀察有什么共同的特征。

教師提出問題9：從形的角度看;從線段的角度看;從角的角度看。

學生根據(jù)問題，紛紛交流，充分討論，順利完成旋轉(zhuǎn)性質(zhì)的歸納。

（學生合作交流展示）

“旋轉(zhuǎn)前后全等”“對應點與旋轉(zhuǎn)中心所成線段相等”;

“對應點與旋轉(zhuǎn)中心所成的角度相等;都是等于旋轉(zhuǎn)角”……

教師演示：已知點A，O，畫出點A繞著點O順時針方向旋轉(zhuǎn)90°后的圖。

“問題引領”下的課例研究

問題10：老師剛才如何畫出這個點的旋轉(zhuǎn)？

眾生：連線，畫角，截取。

問題11：線段的旋轉(zhuǎn)怎么畫？三角形的旋轉(zhuǎn)怎么畫？

（學生交流）

學生：轉(zhuǎn)為點的旋轉(zhuǎn)，因為線段可以由兩個特征點確定，三角形可以由三個特征點確定形狀。

教學分析：通過由淺入深分層次、有梯度的問題，學生充分交流思考，數(shù)學思維被充分調(diào)動。在線段、三角形的轉(zhuǎn)化活動中明確特征點的旋轉(zhuǎn)，通過老師的示范、問題的引領、同學思想交流的碰撞，大部分同學能夠在問題中用概念作出判斷，用概念解決問題，實現(xiàn)概念的鞏固應用。學生在不斷分析、思考中經(jīng)歷新知內(nèi)化的過程，逐步加深對旋轉(zhuǎn)概念的認識，漸次發(fā)展其轉(zhuǎn)化、分析問題等重要數(shù)學核心素養(yǎng)與能力。

4.拓展延伸，運用旋轉(zhuǎn)

已知Rt△ABC，∠BCA=90°，∠ABC=30°，AC=2，P為三角形內(nèi)一點，

（1）請作出△APB繞著A點順時針旋轉(zhuǎn)60°后的圖形△AP′B′;

（2）請根據(jù)你的作圖提出一個數(shù)學問題。

（學生在學案上鞏固作圖，并根據(jù)圖形積極提出問題）

“連接BB，求四邊形ACBB的面積。”

“求證ΔABB′為等邊三角形。”

“連接PP，求證ΔAPP′為等邊三角形。”

……

問題12：當P為三角形內(nèi)任一點，求PA+PB+PC最小值。

（學生議論紛紛）

5.課堂小結，展望旋轉(zhuǎn)

今天你有什么收獲？明天會學什么？回頭看這節(jié)課，你經(jīng)歷了什么？

“認識了旋轉(zhuǎn)，會畫旋轉(zhuǎn)。”

“明天會學什么？用旋轉(zhuǎn)解決最后老師留下的思考題。”

“從生活實例抽象出旋轉(zhuǎn)定義，研究旋轉(zhuǎn)性質(zhì)，總結了旋轉(zhuǎn)的作圖。我真切地感受到，類比與歸納是數(shù)學學習的重要方法。”

“以后我們還會學習利用旋轉(zhuǎn)解決問題。”

教學分析：作為本章的起始課，通過生活實例，仿照以前的平移、軸對稱的特征，根據(jù)已有經(jīng)驗，讓學生感受到知識學習的“相似性”，增強新知識學習的信心。數(shù)學思想方法始終滲透學習的每一環(huán)節(jié)。引導學生學會提煉數(shù)學思想方法——類比、轉(zhuǎn)化、歸納等，也對后面內(nèi)容作了展望，通過設置思考題激發(fā)欲望，為后續(xù)學習打開思路。

二、教學反思

1.遵循認知規(guī)律，經(jīng)歷概念學習

波利亞指出：“教材呈現(xiàn)在學生面前的大多是嚴格的系統(tǒng)的描述，他們是直截了當?shù)貙懗鼋Y果，隱去了發(fā)現(xiàn)的過程。”本節(jié)課教材內(nèi)容只有不到一頁，所以在安排本節(jié)課內(nèi)容時，讓學生跟著問題探究、發(fā)現(xiàn)、總結、歸納，形成概念，理解性質(zhì)，運用知識。

其實概念既是數(shù)學思維的基礎，又是數(shù)學思維的結果，所以不應該簡單給出定義，應當遵循認知規(guī)律，引導學生參與概念的形成過程，暴露思維活動。如：三角形旋轉(zhuǎn)有幾個對應點？一開始大都認為是三個對應點，經(jīng)過討論、分析，領悟旋轉(zhuǎn)本質(zhì)，這對后面學習性質(zhì)以及今后應用都有很大幫助。

2.從“點全、線聯(lián)、面融”的視角上好概念課

（1）點全：溯源設景引概念，水落石出析概念

概念教學中要找出概念如何產(chǎn)生的。旋轉(zhuǎn)就是從生活中的現(xiàn)象抽象出來的，與前面的學習沒有直接關聯(lián)。定義要點透，即如何下定義，抓住概念本質(zhì)屬性，概念描述的關鍵點要透徹。

（2）線聯(lián)：明析從哪里來，去哪里

在備課中要了解概念在教材中的作用、地位到底是什么，概念往何處走，產(chǎn)生這個概念要干什么、有什么用，即概念的數(shù)學利用價值在哪里。旋轉(zhuǎn)的利用價值首先是為圓做鋪墊，其次旋轉(zhuǎn)是一個全等變換，在初中幾何學習全等變換是一條主線貫穿始終：平移，軸對稱，折疊，旋轉(zhuǎn)。因為全等變換的重要性，所以其也被稱為一種解題方法，我們要在動態(tài)圖形中識別屬于哪一種變換，這樣就可以用它們的一些性質(zhì)來解決問題。所以概念教學的線聯(lián)就是要產(chǎn)生數(shù)學價值。

（3）面融：悟出本質(zhì)，融會貫通

概念教學要把之前學過的內(nèi)容融匯在一起，即要知道它承前是什么，也要知道啟后是什么。把整個知識體系，即教材架構理清楚。在概念學習時可以類比之前的平移變換、軸對稱變換。學了概念后要解決什么問題，通過小結的設問，給學生一個暗示或伏筆，讓學生心生向往。本節(jié)教學設計的后面設置了開放問題：根據(jù)你的作圖提出一個數(shù)學問題。這有助于對學生們概念結構層面有一個承前啟后的整體認識，從而引導其掌握概念學習的思想方法，提高“四能”，進而發(fā)展“六核”——數(shù)學學科核心素養(yǎng)。

總之，本節(jié)課以“問題引領”為載體，抓住概念生成，注重概念關鍵點的理解，圍繞概念教學本質(zhì)設置問題，探究過程中追求從簡單到復雜，提煉出數(shù)學結果本質(zhì)現(xiàn)象，圓滿達成教學目標。相信只要老師們備課時深研教材，設置合理性問題，引導、激勵學生主動參與，從而獲取思維活動經(jīng)驗，提高探究問題、解決問題的能力，就一定能讓基本思想和核心素養(yǎng)在平時教學中落地生根。